«преобразование выражений с использованием формул сложения»

«ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ С ИСПОЛЬЗОВАНИЕМ ФОРМУЛ СЛОЖЕНИЯ»

Филимонова Ольга Николаевна

преподаватель математики

ЭПИГРАФ:

« ЕСЛИ ВЫ ХОТИТЕ УЧАСТВОВАТЬ В БОЛЬШОЙ ЖИЗНИ, ТО НАПОЛНЯЙТЕ СВОЮ ГОЛОВУ МАТЕМАТИКОЙ, ПОКА ЕСТЬ К ТОМУ ВОЗМОЖНОСТЬ. ОНА ОКАЖЕТ ВАМ ПОТОМ ОГРОМНУЮ ПОМОЩЬ ВО ВСЕЙ ВАШЕЙ РАБОТЕ.»

ЦЕЛИ :

• Актуализация опорных знаний о формулах сложения, формирование умений использовать формулы сложения для преобразования выражений и доказательства тождеств.

ЗАДАНИЕ: НАЙДИТЕ СООТВЕТСТВИЕ.

1 . Sin(α+β)

1. CosαCosβ + SinαSinβ

2. Sin(α-β)

2. tgα + tgβ

1- tgαtgβ

3. Cos(α+β)

3. SinαCosβ + CosαSinβ

4 . Cos(α - β)

4. CosαCosβ - SinαSinβ

5. tg(α+β)

5. tgα - tgβ

1+ tgαtgβ

6 . tg(α - β)

6. SinαCosβ - CosαSinβ

7. Sinα + Sinβ

8. Cosα - Cosβ

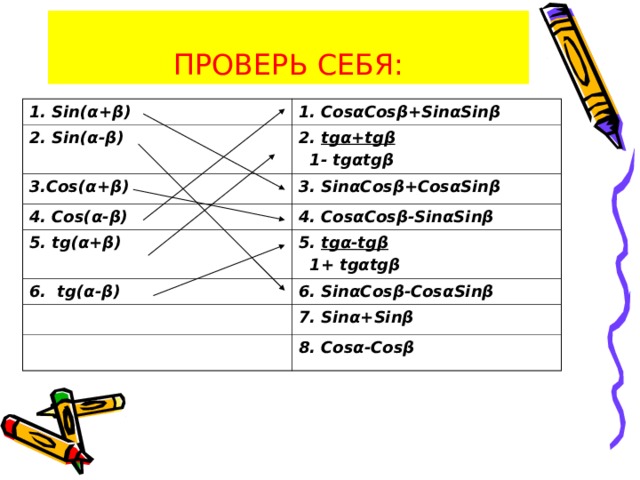
ПРОВЕРЬ СЕБЯ:

1 . Sin(α+β)

2. Sin(α-β)

1. CosαCosβ + SinαSinβ

3. Cos(α+β)

2. tgα + tgβ

1- tgαtgβ

4 . Cos(α - β)

3. SinαCosβ + CosαSinβ

4. CosαCosβ - SinαSinβ

5. tg(α+β)

6 . tg(α - β)

5. tgα - tgβ

1+ tgαtgβ

6. SinαCosβ - CosαSinβ

7. Sinα + Sinβ

8. Cosα - Cosβ

ФОРМУЛЫ

Sin(α+β) = SinαCosβ + CosαSinβ

Sin(α-β) = SinαCosβ - CosαSinβ УЧТЁМ, ЧТО КАЖДАЯ ИЗ

Cos(α+β) = CosαCosβ - SinαSinβ УКАЗАННЫХ ФОРМУЛ ПРИ-

Cos(α - β) = CosαCosβ + SinαSinβ МЕНЯЕТСЯ НА ПРАКТИКЕ

tg(α+β) = tgα + tgβ

1- tgαtgβ КАК «СЛЕВА НАПРАВО», ТАК

И «СПРАВА НАЛЕВО».

tg(α - β) = tgα - tgβ

1+ tgαtgβ

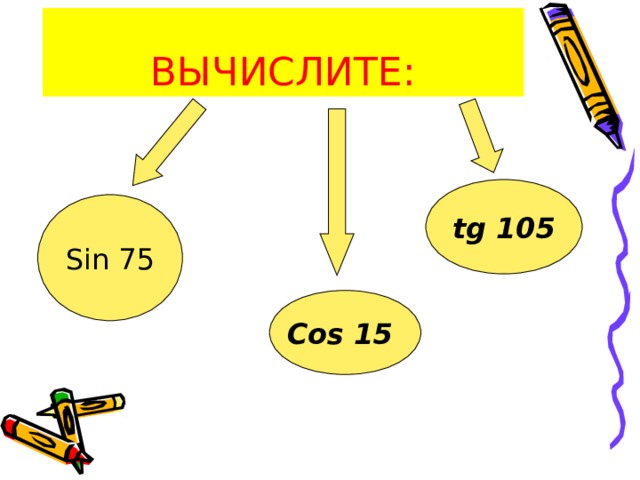
ВЫЧИСЛИТЕ:

tg 105

Sin 75

Cos 15

ИНСТРУКТАЖ:

1 . Получить задание следующего уровня сложности можно только после того, как верно будет решено предыдущее.

2. Для получения оценки «три» необходимо научиться решать первые две задачи.

3. Домашнее задание будет выдано дифференцированно, в зависимости от уровня заданий, решенных на уроке.

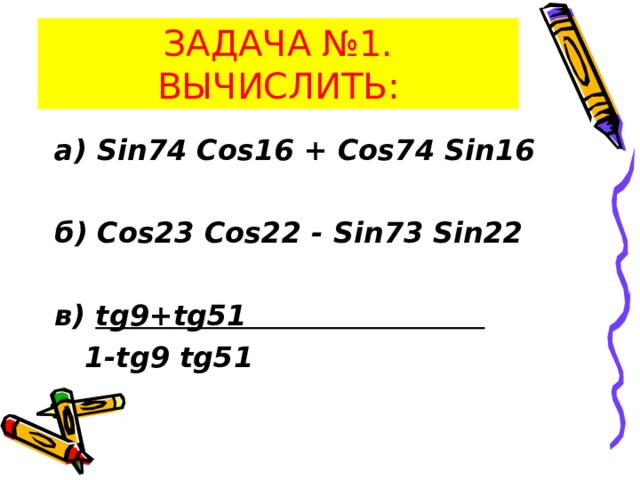
ЗАДАЧА №1. ВЫЧИСЛИТЬ:

а) Sin 74 Cos 16 + Cos 74 Sin 16

б) Cos 23 Cos 22 - Sin 73 Sin 22

в) tg 9+ tg 51

1- tg 9 tg 51

ЗАДАЧА №2. УПРОСТИТЕ ВЫРАЖЕНИЕ:

а) Sin(α+β) – SinαCosβ

б) Sin (п/6- α )-1/2 Cosα

в) tg 2,22- tg 0,92

1+ tg 2,22 tg 0,92

ЗАДАЧА №3. ДОКАЖИТЕ ТОЖДЕСТВО:

а) Cos(α - β) + Sin (- α ) Sinβ = CosαCosβ

б) Sin(α-β) - Sin(α+β) =-2 CosαSinβ

ЗАДАЧА №4. УПРОСТИТЕ ВЫРАЖЕНИЕ:

а) Sin(α-β) +2 CosαSinβ

2 CosαCosβ - Cos(α - β)

б) tg (45+ α )- tgα

1+ tg (45+ α ) tgα

ВОПРОСЫ:

• КАКИЕ ТИПЫ ЗАДАЧ РАССМОТРЕННЫ НА УРОКЕ?

• КАКИЕ ФОРМУЛЫ ИСПОЛЬЗОВАЛИСЬ ДЛЯ РЕШЕНИЯ ПЕРЕЧИСЛЕННЫХ ЗАДАЧ?

3. НАЗОВИТЕ ЭТИ ФОРМУЛЫ.

ДОМАШНЕЕ ЗАДАНИЕ

Упростите выражение:

• Sin(α + β) - SinβCosβ

Sin(α - β) + CosαSinβ

Докажите тождество:

2) Cosα -2 Cos (п/3+ α ) =- tgα

2 Sin ( α -п/6)- Sinα