Преобразование графика квадратичной функции

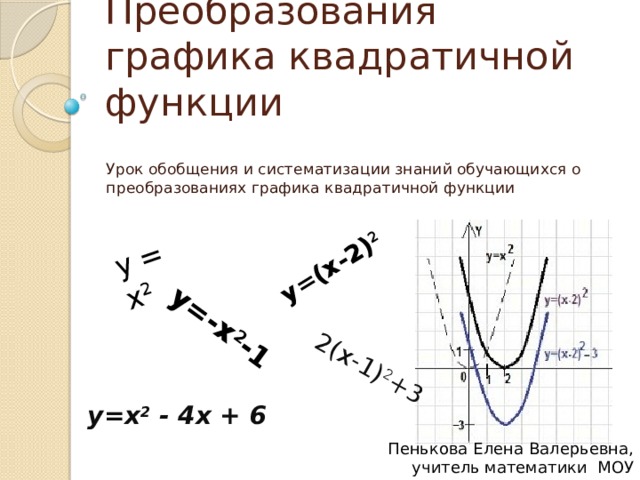
у = х 2

у=-х 2 -1

у=(х-2) 2

2(х-1) 2 +3

Преобразования графика квадратичной функции

Урок обобщения и систематизации знаний обучающихся о преобразованиях графика квадратичной функции

у=х 2  - 4х + 6

Пенькова Елена Валерьевна,

учитель математики МОУ Тоншаевская СОШ

Повторим:

График какой из функции получим, если параллельно перенесем график функции у=х 2 на 2 единицы вправо и на 3 вверх:

• А) у=(х+2) 2 +3
• Б) у=(х-2) 2 -3
• В) у=(х-3) 2 -2
• Г) у=(х-2) 2 +3

Повторим:

Укажите координаты вершины параболы:

• А) у=х 2 -11
• Б) у=(х-3) 2 +8
• В) у=(х+4) 2
• Г) у=(х+1) 2 -9

(0; -11)

(3; 8)

(-4; 0)

(-1; -9)

Повторим:

Построить графики функций в одной системе координат и сделать выводы об их расположении.

• 1 группа: у=х 2 , у=2х 2 , у= -х 2

• 2 группа: у=х 2 , у=х 2 +1, у=х 2 -1

• 3 группа: у=х 2 , у=(х+1) 2 , у=(х-1) 2 .

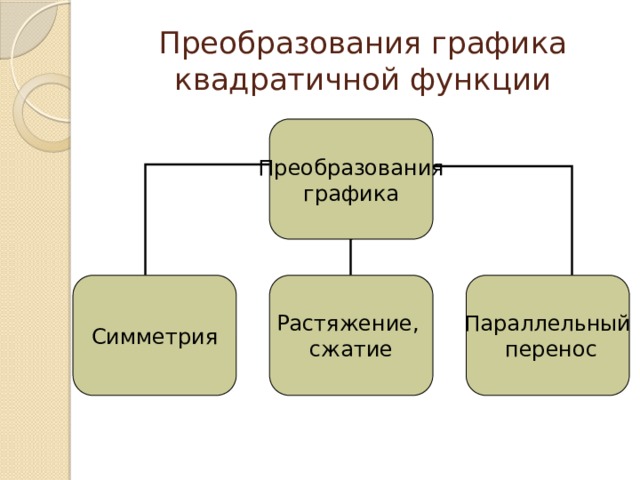
Преобразования графика квадратичной функции

Преобразования

графика

Симметрия

Растяжение,

Параллельный

сжатие

перенос

1, сжатие в 1/а раз, если 0 у=х 2 +а Сдвиг вдоль оси ОУ на а единиц вверх, если а 0; на IаI единиц вниз, если а у=(х+а) 2 Сдвиг вдоль оси ОХ на а единиц влево, если а 0; на IаI единиц вправо, если а " width="640"

Преобразования графика квадратичной функции

Функция

Преобразование графика функции у=х 2

у=-х 2

Симметрия относительно оси ОХ

у=ах 2

Растяжение графика вдоль оси ОУ в к раз, если а 1, сжатие в 1/а раз, если 0

у=х 2 +а

Сдвиг вдоль оси ОУ на а единиц вверх, если а 0; на IаI единиц вниз, если а

у=(х+а) 2

Сдвиг вдоль оси ОХ на а единиц влево, если а 0; на IаI единиц вправо, если а

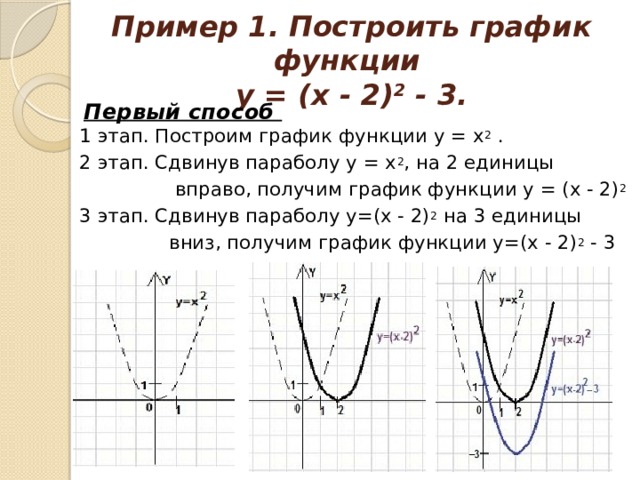
Пример 1. Построить график функции  у = (х - 2) 2  - 3.

Первый способ 1 этап. Построим график функции у = х 2  .

2 этап. Сдвинув параболу у = х 2 , на 2 единицы

вправо, получим график функции у = (х - 2) 2  

3 этап. Сдвинув параболу у=(х - 2) 2  на 3 единицы

вниз, получим график функции у=(х - 2) 2  - 3 

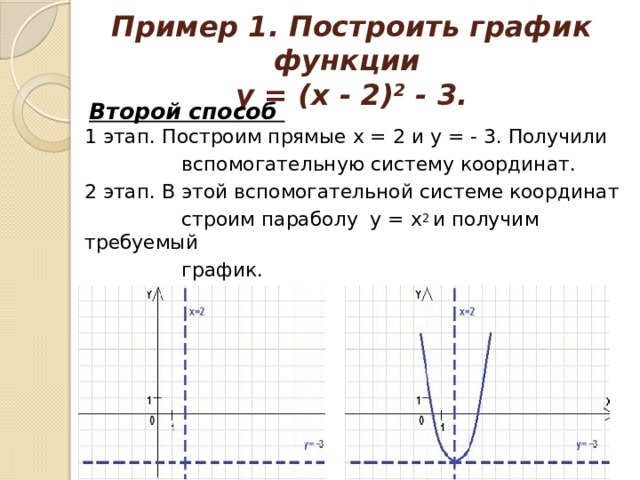
Пример 1. Построить график функции  у = (х - 2) 2  - 3.

Второй способ 1 этап. Построим прямые х = 2 и у = - 3. Получили

вспомогательную систему координат.

2 этап. В этой вспомогательной системе координат

строим параболу  у = х 2  и получим требуемый

график.

Физкультминутка

• Растяжение графика – руки в стороны
• Перенос графика вверх – руки вверх
• Перенос графика вниз – присесть
• Перенос графика вправо – поворот

туловища направо

• Перенос графика влево – поворот

туловища налево

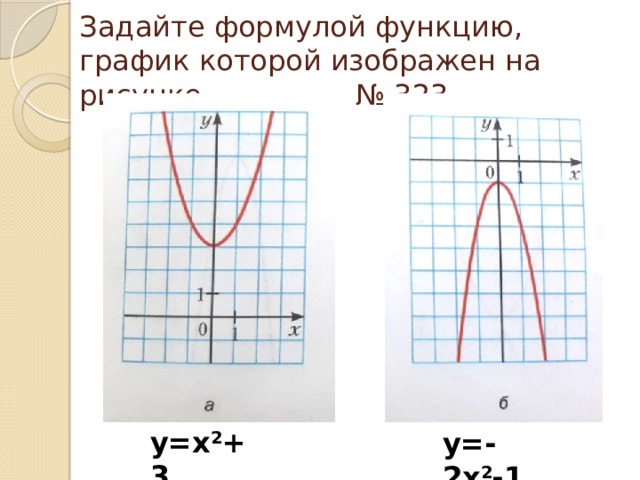
Задайте формулой функцию, график которой изображен на рисунке № 323

у=х 2 +3

у=-2х 2 -1

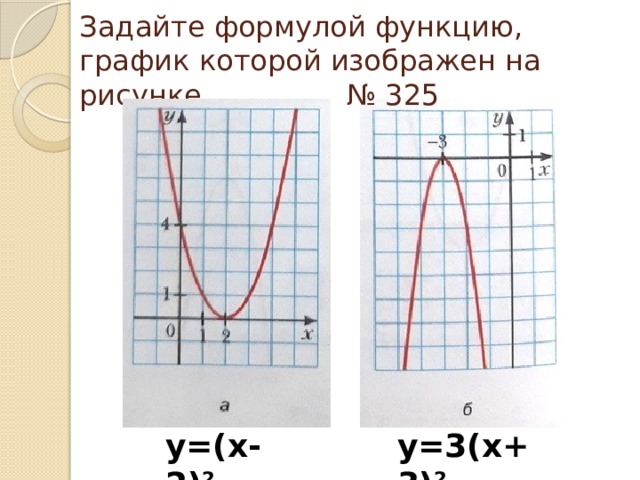
Задайте формулой функцию, график которой изображен на рисунке № 325

у=(х-2) 2

у=3(х+3) 2

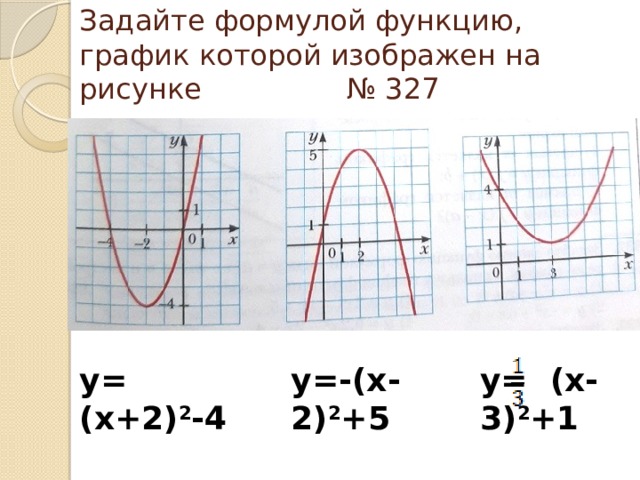
Задайте формулой функцию, график которой изображен на рисунке № 327

у= (х+2) 2 -4

у=-(х-2) 2 +5

у= (х-3) 2 +1

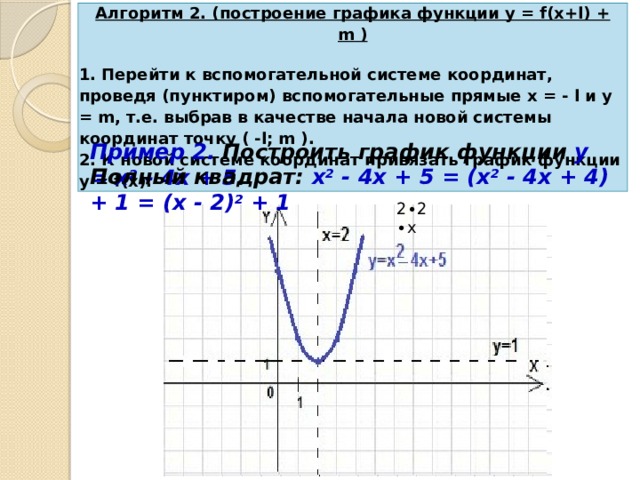
Алгоритм 2. (построение графика функции y = f(x+l) + m )

1. Перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые x = - l и y = m, т.е. выбрав в качестве начала новой системы координат точку ( -l; m ). 2. К новой системе координат привязать график функции у = f(x).

Пример 2.  Построить график функции  у = х 2  - 4х + 5 .

Полный квадрат:  х 2  - 4х + 5 = (х 2  - 4х + 4) + 1 = (х - 2) 2  + 1

2∙2∙х

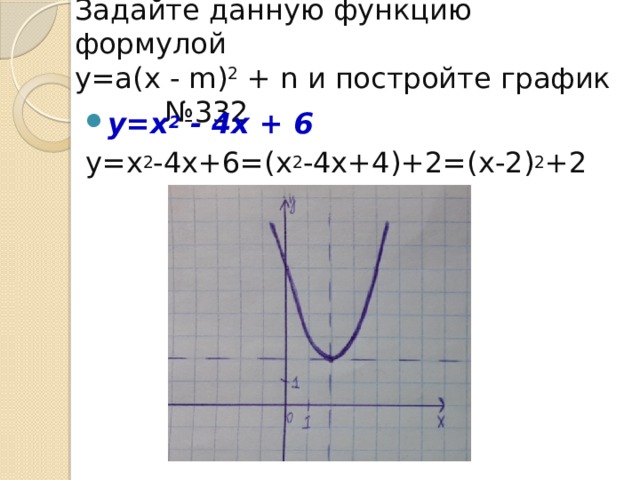
Задайте данную функцию формулой у=а (х - m) 2  + n и постройте график №332

• у=х 2  - 4х + 6

у=х 2 -4х+6=(х 2 -4х+4)+2=(х-2) 2 +2

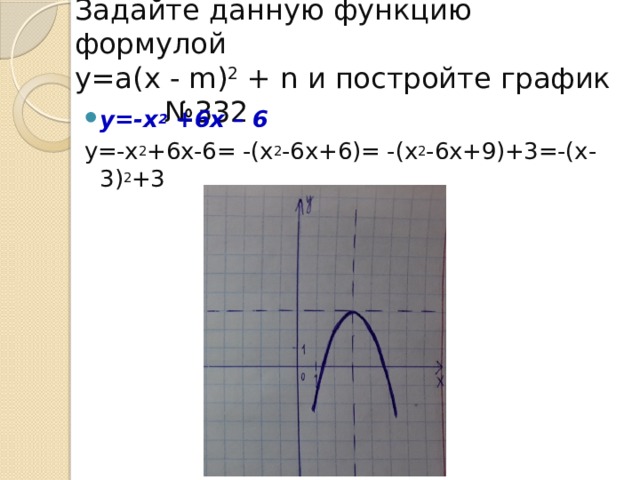
Задайте данную функцию формулой у=а (х - m) 2  + n и постройте график №332

• у=-х 2  +6х – 6

у=-х 2 +6х-6= -(х 2 -6х+6)= -(х 2 -6х+9)+3=-(х-3) 2 +3

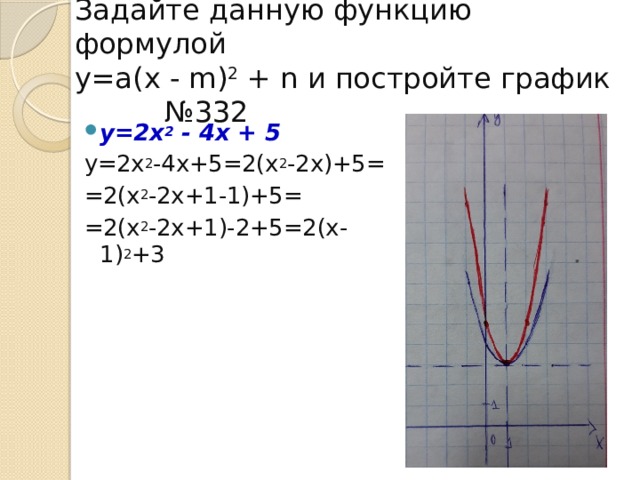
Задайте данную функцию формулой у=а (х - m) 2  + n и постройте график №332

• у=2х 2  - 4х + 5

у=2х 2 -4х+5=2(х 2 -2х)+5=

=2(х 2 -2х+1-1)+5=

=2(х 2 -2х+1)-2+5=2(х-1) 2 +3

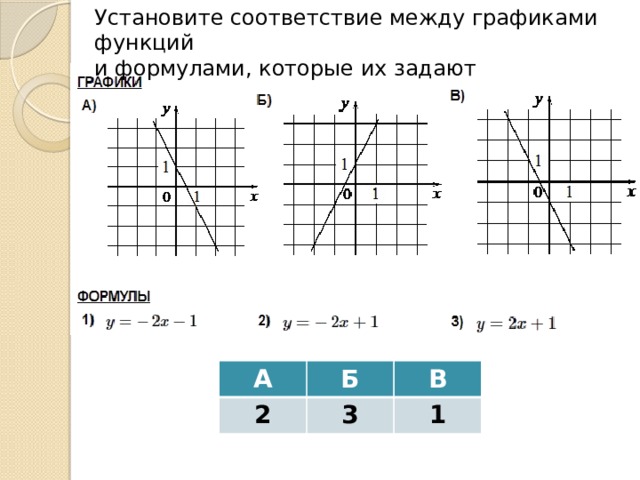
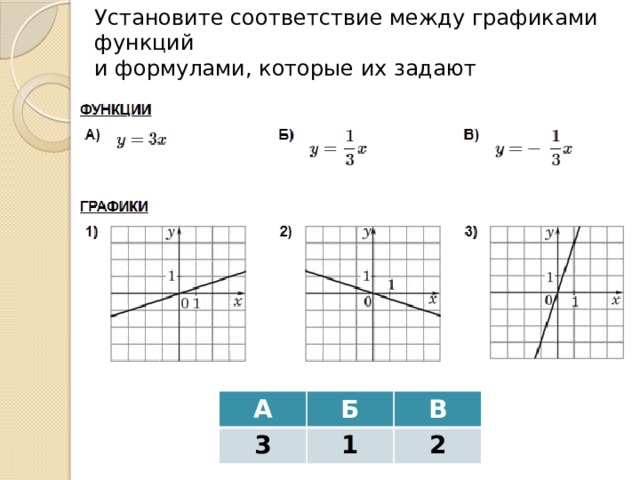
Установите соответствие между графиками функций

и формулами, которые их задают

А

2

Б

В

3

1

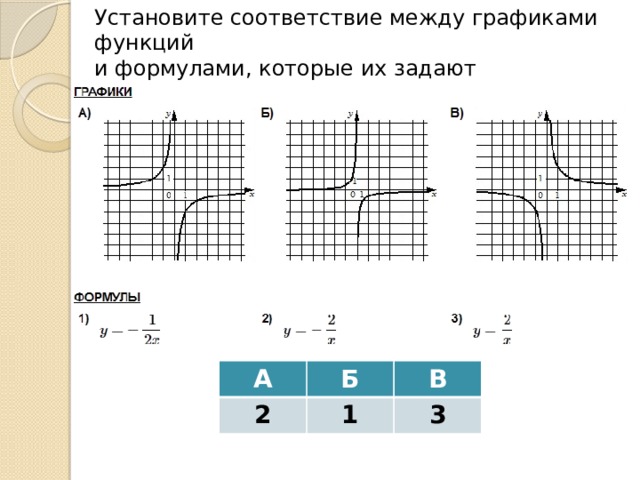
Установите соответствие между графиками функций

и формулами, которые их задают

А

3

Б

В

1

2

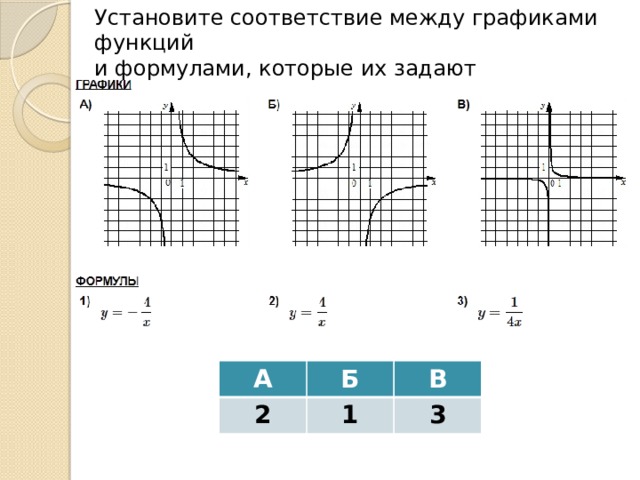
Установите соответствие между графиками функций

и формулами, которые их задают

А

2

Б

В

1

3

Установите соответствие между графиками функций

и формулами, которые их задают

А

2

Б

В

1

3

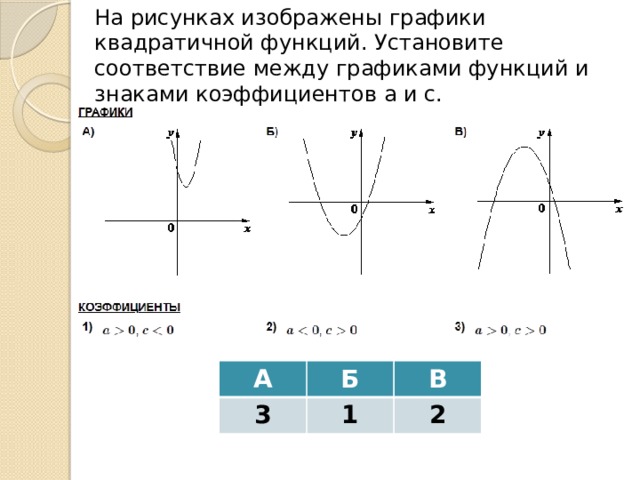
На рисунках изображены графики квадратичной функций. Установите соответствие между графиками функций и знаками коэффициентов а и c.

А

3

Б

В

1

2

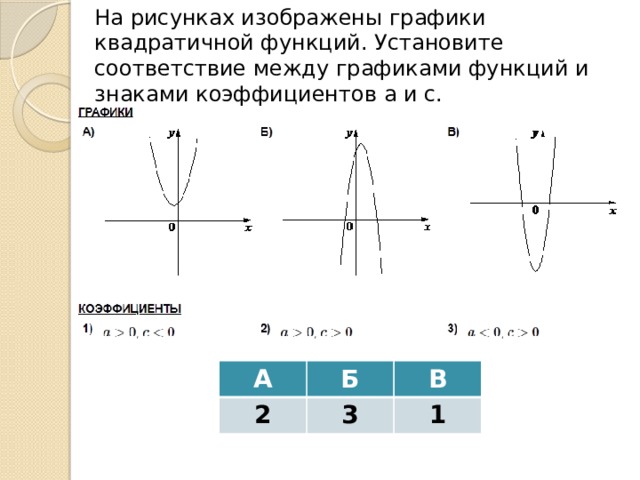
На рисунках изображены графики квадратичной функций. Установите соответствие между графиками функций и знаками коэффициентов а и c.

А

2

Б

В

3

1

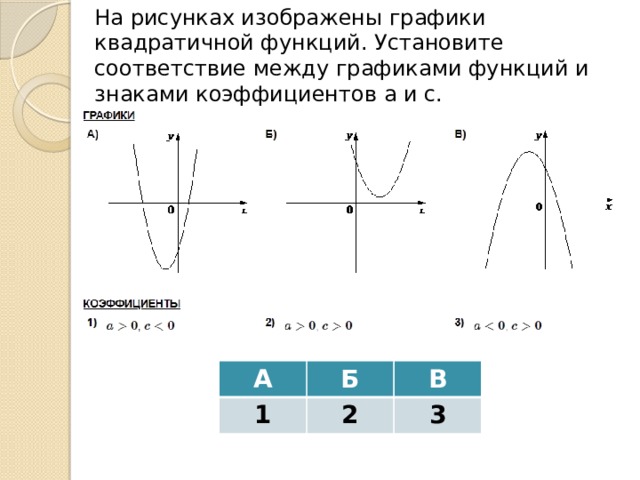
На рисунках изображены графики квадратичной функций. Установите соответствие между графиками функций и знаками коэффициентов а и c.

А

1

Б

В

2

3

Домашнее задание:

• 324, 325, 329, 333

Спасибо за внимание!