Конспект урока по математике и информатике "Преобразование графика квадратичной функции"

Характеристика класса

Общеобразовательный класс со средним показателем качества обученности

Цель урока: Создание условий для развития интересов и способностей учащихся к математике на основе изучения графиков квадратичной функции, формирование  умений исследования функций и построения их графиков в среде электронных таблиц.

развитие метапредметных связей.

Учебные задачи, направленные на развитие учащихся

(планируемые результаты):

Личностные:

• развитие у учащихся самостоятельности в приобретении новых знаний и практических умений

Метапредметные:

развитие у учащихся умений:

• формулировать гипотезы и оценивать их верность с точки зрения полученной в ходе исследования информации;

• проводить исследование по предложенному плану;

• на основании результатов эксперимента формулировать вывод;

• развивать коммуникативные навыки при организации работы в группах.

Предметные:

• формирование у учащихся умений строить графики квадратичных функций с помощью преобразований (симметрия, перенос) и в среде электронных таблиц;

Методы:

Словесный, проблемно-поисковый, исследовательский, объяснительно-иллюстративный, использование ИКТ.

Материалы:

Оборудование:

• учебник алгебры 9 класс,

• листы с заданиями для исследовательской работы в группах;

• карточки для рефлексии.

• компьютер с офисным приложением Excel

• компьютеры, мультимедийный проектор

Формы работы:

Технология реализации:

самостоятельная, фронтальная работа, групповая, работа в парах.

Личностно – ориентированное обучение.

Этапы урока

Задачи этапа

Деятельность учителя

Деятельность учащихся

УУД

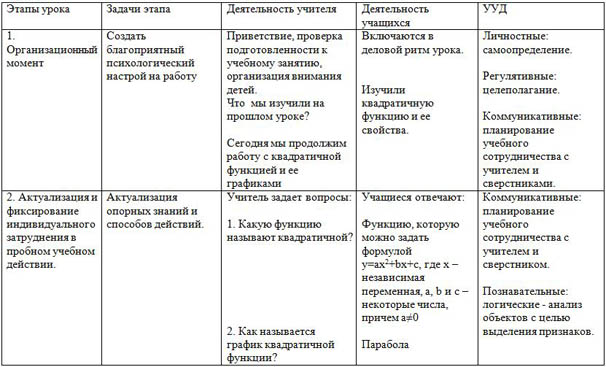
1. Организационный момент

Создать благоприятный психологический настрой на работу

Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.

Что мы изучили на прошлом уроке?

Сегодня мы продолжим работу с квадратичной функцией и ее графиками

Включаются в деловой ритм урока.

Изучили квадратичную функцию и ее свойства.

Личностные: самоопределение.

Регулятивные: целеполагание.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии.

Актуализация опорных знаний и способов действий.

Учитель задает вопросы:

1. Какую функцию называют квадратичной?

2. Как называется график квадратичной функции?

3. Сформулируйте свойства функции у=ах² при а0?

4. Как можно получить график функции у=ах² из параболы у=х², если а1 и если 0a

Учащиеся отвечают:

Функцию, которую можно задать формулой y=ax²+bx+c, где х – независимая переменная, а, b и с – некоторые числа, причем а≠0

Парабола

Учащиеся формулируют свойства.

Растяжением от оси Х в а раз, если, а1 и сжатием к оси Х в 1/а раз, если 0a

Коммуникативные: планирование учебного сотрудничества с учителем и сверстником.

Познавательные: логические - анализ объектов с целью выделения признаков.

3.Целеполагание и мотивация

Обеспечение мотивации учения детьми, принятие ими целей урока.

Как вы думаете одинаковы ли графики у функций: у=х²+3 и у=(х+3)².

Проблема: А как построить график квадратичной функции у=ах²+n, у=а(х-m)², у=а(х-m)²+n

Цель урока

-Какая цель нашего урока?

Строят графики функций в тетрадях и сравнивают их.

Формулируют цель урока: мы будем учиться строить графики функций у=ах²+n, у=а(х-m)², у=а(х-m)²+n.

Регулятивные: целеполагание.

Коммуникативные: постановка вопросов.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические - формулирование проблемы.

4. Усвоение новых знаний и способов усвоения

Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы: построение графиков квадратичной функции

-Итак, тема нашего урока созвучна цели урока.

-Как называется тема нашего урока?

Записываем в тетрадь тему урока.

Понятно, что строить такие графики по точкам нецелесообразно, и мы сегодня выведем общие правила как именно получить графики квадратичных функций из графика функции у=ах² .

Как это сделать?

Записывают в тетрадь.

Тема урока: «Построение графиков квадратичной функции»

Для этого нам надо построить много графиков, сравнить их, проанализировать и сделать выводы.

Коммуникативные: постановка вопросов, инициативное сотрудничество.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство.

Регулятивные: планирование, прогнозирование.

5.Первичное закрепление

Установление правильности и осознанности изучения темы.

Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.

У нас сегодня необычный урок. Мы попробуем объединить знания, полученные на уроках алгебры и информатики.

Для того чтобы построить много графиков за короткое время будем использовать электронные таблицы Excel.

А теперь вспомним алгоритм построения графика функции с помощью электронных таблиц Excel».

Перед вами ставится задача – смоделировать на компьютере поведение графика квадратичной функции при изменении её параметров.

Далее ученикам дается задание для практической работы, они должны построить графики функций и сделать вывод, по какой оси, на сколько и в каком направлении будет сдвигаться график в зависимости от значений m,n.

Отвечают:

Составить таблицу значений функции;

Выделить таблицу, построить график   

Учащиеся работают за компьютерами, используя раздаточный материал.

Регулятивные: контроль, оценка, коррекция.

Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.

Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера.

6. Организация первичного контроля

Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков.

Самостоятельная работа по карточкам.

Самопроверка.

Самостоятельное решение в карточках

Самопроверка.

Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;

Личностные: самоопределение.

7. Подведение итогов урока.

Дать качественную оценку работы класса и отдельных обучаемых

-Что изучили сегодня на уроке?

-Кто желает сформулировать правила получения графика функции у=а(х-m)²+n из графика функции у=ах²?

Оправдано ли при построении данных графиков  и решении уравнений применение компьютера? Как легче построить графики: в тетради самостоятельно или при помощи компьютера?

Сегодня на уроке мы рассмотрели использование прикладной программы Excel при решении практической задачи и ещё раз убедились в том, что применение компьютеров при решении задач пользователя экономит наше время, и форма представления результатов удобна для восприятия.

Оценить отдельных учащихся

Отвечают на поставленные вопросы

Регулятивные: оценка-осознание уровня и качества усвоения; контроль

8. Информация о домашнем задании

Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.

№95

9. Рефлексия

Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.

Выберете, какая парабола вам ближе по результату усвоения темы урока.

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли.

Познавательные: рефлексия.