Получите свидетельство
Вход
ПЛАН – КОНСПЕКТ УРОКА
на тему:
«Прямоугольные треугольники и некоторые их свойства»
Выполнил: Губеев С.П.
Тема: «Прямоугольные треугольники».
Дата: 6 марта 2017 года.
Класс: 7-ой В.
Тема урока: «Прямоугольные треугольники и некоторые их свойства».
Тип урока: урок изучения нового материала.
Форма урока: традиционный.
Цели урока:
Образовательная:
1) рассмотреть свойства прямоугольных треугольников;
2) научить решать задачи на применение свойства прямоугольных треугольников.
Воспитательная:
развить интерес к математике; формирование аккуратности и умение организовывать свое рабочее место; трудолюбие.
Развивающая:
развитие логического мышления; развитие самостоятельности и творческого начала в умственной деятельности.
Оборудование: мел, доска, тряпка, учебник, план – конспект.
План урока:
1. Организационный момент (3 мин.).
2. Актуализация знаний (5 мин.).
3. Изучение новой темы (15 мин.).
4. Закрепление изученного материала (16 мин.).
5. Домашнее задание (1мин.).
6. Подведение итогов урока (5 мин.).
Ход урока.
1. Организационный момент.
- Здравствуйте! Садитесь! Кто сегодня дежурный? Кто сегодня отсутствует на уроке?
2. Актуализация знаний.
Сейчас все смотрим на доску и решим задачи по чертежам (чертежи заранее начерчены на доске):
1. Рис. 4. 111. Найти:
2. Рис. 4. 112. Найти:
3. Рис. 4. 113.
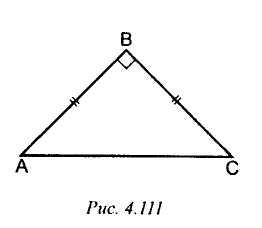
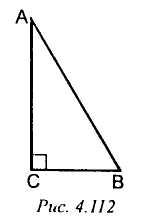
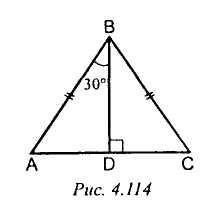
4. Рис. 4. 114. Доказать: AD = 1/2 АВ.
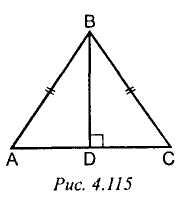
5. Рис. 4. 115. AD = 1/2 АВ. Найти: углы ABD.
Цель решения данных задач - подготовить учащихся к изучению и доказательству свойства прямоугольных треугольников.
3. Изучение нового материала.
Чтобы сформулировать свойства прямоугольного треугольника, докажем самостоятельно данные задачи.
Задача 1
Докажите, что в прямоугольном треугольнике сумма острых углов равна 90°.
Задача 2
Докажите, что катет в прямоугольном треугольнике, лежащий против угла в 30°, равен половине гипотенузы.
Задача 3
Докажите, что, если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Мы рассмотрели различные способы решения данных задач.
И через эти решения мы можем сформулировать свойства
прямоугольных треугольников.
4. Закрепление изученного материала
1. Сейчас устно решим задачи по готовым чертежам:
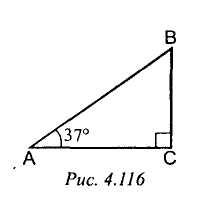
1) Рис. 4. 116. Найти:
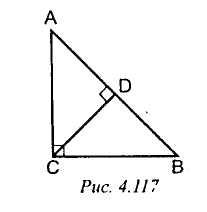
2) Рис. 4. 117. Найти:
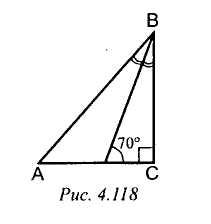
3) Рис. 4. 118. Найти: CAB.
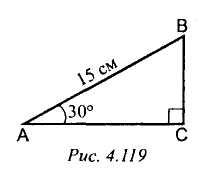
4) Рис. 4. 119. Найти: ВС.
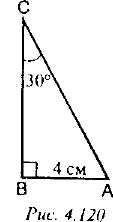
5) Рис. 4. 120. Найти: АС.
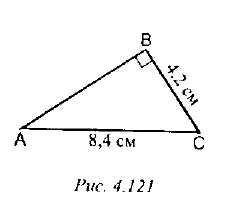
6) Рис. 4. 121. Найти:
Решить задачу № 257 (один ученик работает у доски,
остальные в тетрадях).
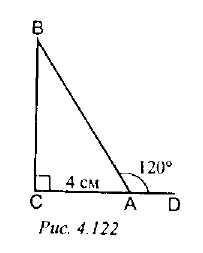
Задача №257 Рис. 4. 122.
Дано: АВС, Найти: АС, АВ.
Решение: тогда
АВС- прямоугольный (
Катет AС лeжит против угла в 30° и он равен половине гипотену¬зы, т. е. АС= 1/2 АВ. Т. к. АС+ АВ= 18 см, то 1/2 АВ + АВ= 18 см, отсюда АВ= 12 см, АС = 6 см.
Ответ: АВ = 12 см, АС= 6 см.
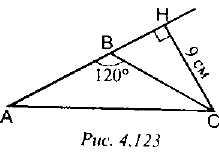
3. Самостоятельно решить задачи № 259, 260. Задача № 259
Решение (см. рис. 4. 123):
ABC - равнобедренный, т. е.
АСН- прямоугольный, в нём
против угла в 30°, значит, АС = 2НС= 18 см. Ответ: 18 см.
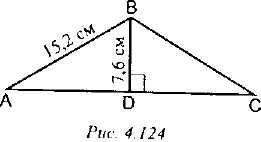
Задача № 260
Решение (см. рис. 4. 124):
АВС- прямоугольный, BD = 1/2 АВ, тогда /А = 30°.
АВС- равнобедренный, тогда
Дополнительные задачи
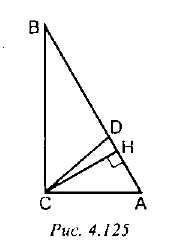
Задача 1
Найти углы прямоугольного треугольника, если угол между биссектрисой и высотой, проведенными из вершины прямого угла, равен 15°.
Решение (см. рис. 4. 125):
CD - биссектриса, СН- высота,
HСA - прямоугольный, в нем
Ответ: 30°, 60°, 90°.
Задача 2
В равнобедренном треугольнике один из углов 120°, а основание равно 4 см. Найдите высоту, проведенную к боковой стороне.
Решение (см. рис. 4. 126):
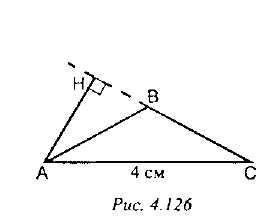
120° - угол при вершине равнобедренного треугольника, тогда
Ответ: 2 см.
Задача 3
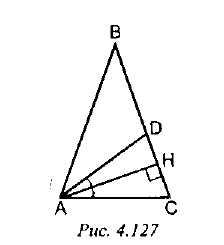
Высота, проведенная к боковой стороне равнобедренного треугольника, делит пополам угол между основанием и биссектрисой. Найдите углы равнобедренного треугольника. Решение (см. рис. 4. 127):
AD - биссектриса
=
=1/4
ABC - равнобедренный, поэтому
Ответ: 72°, 72°, 36°.
Домашнее задание
1. § 34, вопросы 10, 11.
2. Решить задачи № 255, 256, 258.
3. Дополнительные задачи:
Задача 1
Докажите, что, если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.
Дано: СМ = ВМ = МЛ (см. рис. 4. 128).
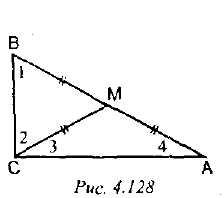
Доказать: АВС- прямоугольный.
Подведение итогов урока.
- За активную работу на уроке получают оценки: …
-Урок окончен.
- До свидания!
Прямоугольные треугольники и некоторые их свойства (112 KB)
0
660
12
Нравится
0
