Урок геометрии в 7 классе
Тема: Сумма углов треугольника
Цель: исследовать свойства треугольника, указать некоторые условия существования треугольника.
Задачи:
повторить с углублением изученного материала теоремы о свойствах параллельных прямых, о сумме углов треугольника и внешнем угле треугольника;
повторить ранее изученные приемы решения задач и познакомиться с новым приемом;
способствовать развитию комбинаторных способностей и пространственного воображения учащихся, умения анализировать, сравнивать, делать выводы;
содействовать выработке умения самоконтроля через умышлено допущены ошибки, которые учащиеся должны обнаружить;
создать условия для поддержания и развития интереса к предмету через представление исторических фактов;
способствовать формированию коммуникативной культуры через организацию работы в группах;
способствовать воспитанию чувства коллективизма, ответственности, активности, взаимопомощи.
Оборудование:
интерактивная доска;
презентация в Power Point;
плакаты с высказываниями ученых, содержащие исторические сведения и познавательную информацию;
раздаточный материал – карточки.
Класс разделен на четыре равные по силе группы. У каждой группы есть ассистент (старшеклассник). На перемене производится жеребьевка. Капитаны случайным образом берут карточки, в которых указаны очередность ответов, номера задач.
Ход урока.
Организационный момент. Проверка готовности к уроку обучающихся, тестирование оборудования
Целеполагание и мотивация учебной деятельности
Учитель: Добрый день! Сегодня у нас последний урок по теме: «Сумма углов треугольника». Этот урок является мостиком между темами «Параллельность прямых» и «Прямоугольные треугольники». Мы повторим признаки и свойства параллельных прямых, вспомним некоторые известные свойства треугольников и, может быть, сумеем открыть новые. Главное место в нашем разговоре займет, конечно же, теорема о сумме углов треугольника.
Актуализация и коррекция опорных знаний
Фронтальная устная работа по решению опорных задач
Обучающимся предложены 4 основные и 2 дополнительные задачи на готовых чертежах. Если группа справилась со своей задачей, можно подумать над дополнительными.
(На экране появляются чертежи, соответствующие задачам. Одна команда отвечает, другие комментируют ответ.)
| а) | 
| б) | 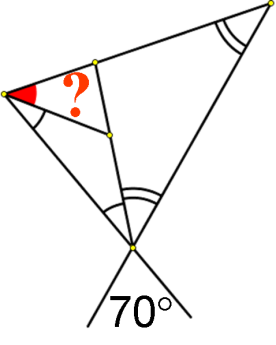
| в) | 
|
| г) | 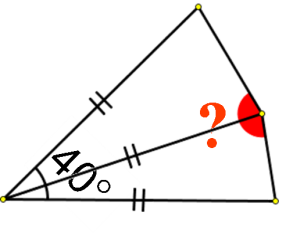
| д) | 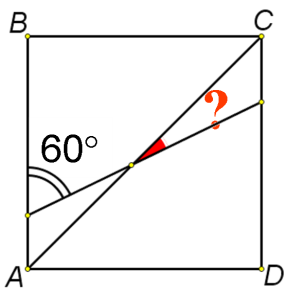
ABCD – квадрат | е) | 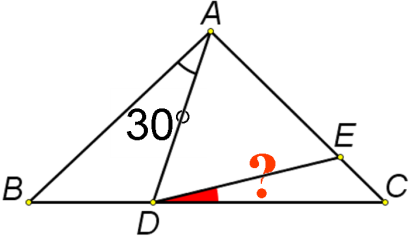
AB=AС, AE=AD |
Учитель: Что вы использовали при решении задач?
После ответов учащихся на экране появляется вывод:
При решении задач «на треугольники» оказываются полезными:
Теорема о внешнем угле треугольника.
Прием «считаем парами».
Презентация домашней задачи.
Теорема о сумме углов треугольника была известна еще в Древней Греции. Геометрия получила широкое развитие, прежде всего, в связи с её практическим применением. Обогащенные геометрическими знаниями, люди производили те или иные расчеты, изобретали приборы. Вот один из них (на экране появляется рисунок). Для измерения величины угла между наклонной и горизонтальными прямыми на местности используют эклиметр, принцип действия которого ясен из рисунка. (ОР – нить с грузиком, отвес) Доказать, что нить ОР показывает на шкале величину искомого угла. Эта дополнительная задача к домашней работе.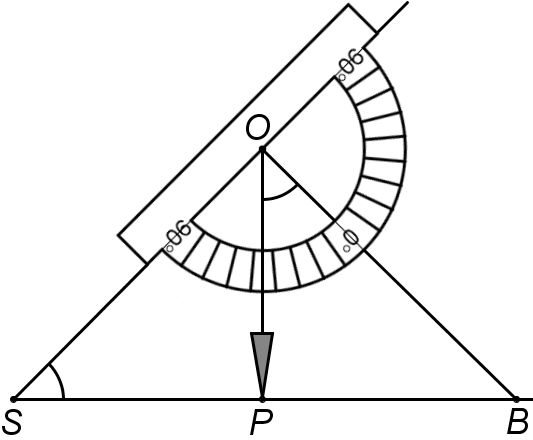
3.Проверка домашнего задания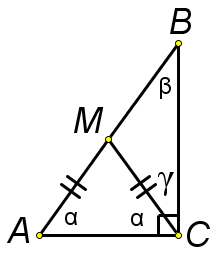
Задача. В прямоугольном треугольнике АВС с прямым углом С, на стороне АВ выбрана точка М так, что МС=МВ. Установить вид треугольника ВСМ.
Решение: А+В+С=180, + + 90=180, + =90. Следовательно = . Треугольник ВСМ – равнобедренный.
Учитель: На основании рассмотренной задачи, сформулируем свойство прямоугольного треугольника (на экране появляется текст с пропусками):
«Если точка М ... (гипотенузы) АВ такова, что МА=МС, то СМ - ... (медиана) треугольника АВС и равна ... (половине гипотенузы)».
Используем этот важный вывод для обоснования самого наглядного доказательства теоремы о сумме углов треугольника с помощью бумажного треугольника.
4.Презентация по теме: «Обоснование «доказательства» теоремы о сумме углов треугольника с помощью листа бумаги» (индивидуальное домашнее задание)
5. Оценка готовности к восприятию нового материала.
Командиры групп подводят промежуточные результаты, отмечают вклад каждого обучающегося в работу на данном этапе.
Учитель: в результате рассмотрения домашней задачи мы установили некоторые свойства прямоугольного треугольника. Подробнее о прямоугольных треугольниках мы поговорим на будущих уроках. А пока еще раз обратимся к теме: «Равнобедренный треугольник».
Решение задач
Работа в группах с представлением результатов у доски и оцениванием решения представителями команд-соперников.
Задача №1. В равнобедренном треугольнике АВС (АВ=ВС) на стороне ВС выбрана такая точка D, что ВАD = 2DАС. Чему может равняться угол В этого треугольника, если известно, что треугольник АВD тоже равнобедренный?
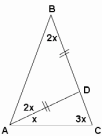
Представитель одной из команд решает задачу на доске. Представители других команд комментируют ответ. 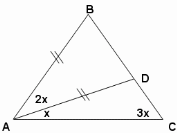
Решение:
а) По теореме о сумме углов треугольника ABD, ADB = 180-4x. ADB – внешний угол треугольника ADC, следовательно ADB = 4x. Составив и решив уравнение, найдем, что B = 45
б) Так как треугольник ADB - равнобедренный, то ABD = ADB = (180-2х):2=90-х. ADB – внешний угол треугольника ADC, следовательно ADB=4x. Составив и решив уравнение, получим что B = 72 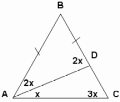
в) Рассматривая полученное аналогичным образом уравнение, приходим к выводу, что такой случай невозможен.
Отв. 72° или 45°.
Учитель: Какие выводы можно сделать на основании решения данной задачи?
(После ответов учащихся на экране появляется вывод)
Если в условии задачи присутствует неопределенность, то необходимо рассматривать все возможные случаи.
Прием «вычисление суммы двумя способами» помогает связать неизвестные величины уравнением
Задача №2. Отрезок AL делит треугольник АВС на два равнобедренных треугольника. Чему может быть равен наибольший угол исходного треугольника, если ВАС=48°?
Учитель: Некто решил эту задачу. Разберитесь в чертежах и закончите решение.
(На экране появляются чертежи)
Решение: а) ALC и ALB смежные, однако + = 180º невозможно, т.к. В и С односторонние было бы АВАС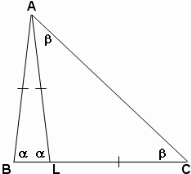
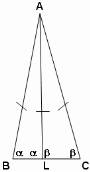
б) ALB – внешний угол треугольника ALC = 2. Сумма углов треугольника ALB равна 180º , поэтому ВАL = 180º - 2. Зная, что ВАС = 48°, составляем уравнение: 180 - 4 + = 48, =44. А=48º, В=44º, С=88º. Проверка: 48+44+88=180. Наибольший угол равен 88º.
Учитель: Я предлагаю вам ознакомиться с третьим случаем, и сделать вывод, который пригодится нам при решении следующей задачи.
в) Так как ∆АСL – равнобедренный, то углы при основании равны. Пусть АСL= АLС=. Так как ∆АВL – равнобедренный, то углы при основании равны. Пусть LАВ= АLВ=.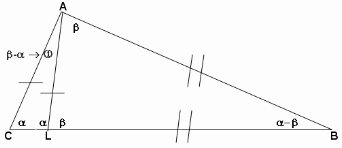
АLВ – внешний угол ∆АСL, следовательно, CAL=-. АLС – внешний угол ∆АВL, следовательно, ABL=-.
Зная, что ВАС=48°, составляем уравнение: 2--48. Зная, что АLС и АLВ смежные, составляем уравнение: +=180
Решаем систему уравнений. Окончательно имеем: А=48º (по условию), В=-=28º, С==104º
Проверка: 48+28+104=180º
Все ли верно?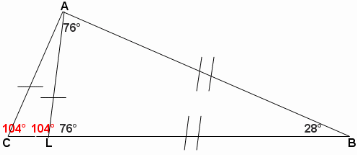
Обучающиеся, многократно читая предложенный текст, проверяя и перепроверяя себя и товарищей, чувствуют что «что-то здесь не так», хотя ошибку не находят.
На экране возникает чертеж с числовыми даными.
После ответов учащихся на экране появляется вывод:
в равнобедренном треугольнике углы при основании могут быть только острыми.
Замечание. Система должна была иметь вид: 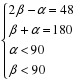 . Дальнейшее решение этой задачи будет рассмотрено на факультативе.
. Дальнейшее решение этой задачи будет рассмотрено на факультативе.
Задача №3. (Закрепление сделанного вывода.) Существует ли выпуклый четырехугольник АВСD и точка М внутри него такие, что МА=АВ, МВ=ВС, МС=СD, МD=АD?
Решение. Так как ∆АВМ, ∆ВСМ, ∆МСD, ∆АМD – равнобедренные, то углы при основании острые. , , , . +++,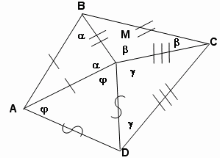
С другой стороны, сумма углов при вершине М равна 360º. Пришли к противоречию.
Ответ: Такого четырехугольника не существует.
После ответов учащихся на экране появляется вывод:
Оценка суммы помогает решить задачу.
Индивидуальная работа с самопроверкой решения
Задача-аукцион. К треугольнику АВС (А=20º, В=50º, С=110º) пристроили равнобедренный треугольник так, что получился новый треугольник. Сколькими способами это можно сделать? Вычислите углы нового треугольника.
Решение задачи каждый ученик выполняет на выданном ему листе с таблицей, в каждой ячейке которой изображен один и тот же треугольник. Постепенно на экране появляются карточки с ответами.
Ответы:
| 
50; 55; 75 | 
50; 60; 70 | 
40; 50; 90 | 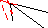
20; 55 105 | 
10; 60; 110 |
| 
20; 70; 90 | 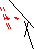
20; 40; 120 | 
25; 45; 110 | 
| 
|
Рефлексия. Группы используют методику «Я, мы, дело» для характеристики учебной деятельности каждого обучающегося, группы, класса в целом. Учитель оценивает работу на уроке, выставляет оценки.


 Получите свидетельство
Получите свидетельство Вход
Вход


















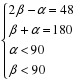 . Дальнейшее решение этой задачи будет рассмотрено на факультативе.
. Дальнейшее решение этой задачи будет рассмотрено на факультативе. 














 Конспект урока по математике по теме «Сумма углов треугольника» (0.34 MB)
Конспект урока по математике по теме «Сумма углов треугольника» (0.34 MB)
 0
0 804
804 83
83 Нравится
0
Нравится
0








