Презентация по математике "Решение уравнения sin x + cos x = 1"

Презентация показывает методы и способы решения данного уравнения.

Презентация содержит девять слайдов.

Решение уравнения sin x + cos x = 1.

Работа педагога дополнительного образования

МБОУ ДОД ДДТ г.Зверево

Куца Фёдора Ивановича.

1) Метод дополнительного угла.

Обе части уравнения делятся на выражение , вводится дополнительный угол

Пример. sin x + cos x = 1.

a = 1, b = 1: = = .

sin x + cos x = .

cos sinx + sin cosx = , sin(x + ) = .

x + = (- 1) n arcsin + πn, n є Z ; x + = (- 1) n + πn, n є Z ;

x = - + (- 1) n + πn, n є Z .

Ответ. x = - + (- 1) n + πn, n є Z.

2 ) Использование универсальной тригонометрической подстановки.

sin x = , cos x = .

Пример. sin x + cos x = 1.

+ = 1, 2 + 1 - = 1 + ,

2 - 2 = 0, 2 ( - 1) = 0.

2 = 0 или - 1 = 0.

1) = 0. = πn, n є Z; x = 2πn, n є Z.

2) = 1. = + πk, k є Z ; x = + 2πk, k є Z.

Ответ. x = 2πn, n є Z; x = + 2πk, k є Z.

3) Сведение к однородному уравнению.

Пример. sinx + cosx = 1.

Используя формулы sinx = 2sin cos , cosx = cos 2 - sin 2

и записывая правую часть уравнения в виде 1= cos 2 + sin 2 , получаем:

2sin cos + cos 2 - sin 2 = cos 2 + sin 2 .

2 sin 2 - 2sin cos = 0.

Вынеся общий множитель за скобки, получим равносильное уравнение 2 sin (sin - cos )= 0.

Откуда 2sin = 0 или sin – cos = 0.

1) sin = 0. = πn, n є Z; x = 2πn, n є Z.

2) sin - cos = 0, sin = cos , tg = 1.

= + πn , n є Z; х = +2πn, n є Z.

Ответ. x = 2πn, x = + 2πn, n є Z;

4)Преобразование суммы в произведение.

Пример. sin x + cos x = 1.

Выразим cos x через sinx, используя формулы приведения: cos x = sin ( - x).

sin x + sin ( - x) = 1;

2 sin cos = 1;

2 sin cos (x - ) = 1;

2∙ ∙ cos (x - ) = 1; cos (x - ) = .

x - = ± arccos +2 n, x = ± +2 n.

x = 2 n, х = + 2 n, n є Z.

Ответ. x = 2πn, x = + 2πn, n є Z.

5) Возведение обеих частей уравнения в квадрат.

Пример. sin x + cos x = 1.

(sin x + cos x ) 2 = 1; sin 2 x + 2sin x cos x + cos x 2 = 1;

sin 2x + 1 = 1; sin 2x = 0.

2x = πn; x = , n є Z.

При возведении уравнения в квадрат получаем

уравнение – следствие, поэтому проведем проверку.

Учитывая, что период функции y = sin x равен 2π, имеем:

1)При х = 0 + 2πn, n є Z, 0 + 1 = 1 верно.

х = 2πn, n є Z – корни уравнения.

2)При х = + 2πn, n є Z, 1+ 0 = 1 верно.

х = + 2πn, n є Z – корни уравнения.

3)При х = π + 2πn, n є Z, 0 - 1 = 1 неверно. х = π + 2πn, n є Z – не являются корнями уравнения.

4)При х = + 2πn, n є Z, -1+ 0 = 1 неверно.

х = + 2πn, n є Z – не являются корнями уравнения.

Ответ. x = 2πn, x = + 2πn, n є Z.

6) Применение формул двойного и половинного аргумента.

Пример. sin x + cos x = 1.

Запишем уравнение в виде: sin x = 1 - cos x .

Сделаем замену: sin x = 2sin cos , 1 - cos x = 2sin 2 .

2sin cos = 2sin 2 ; 2sin cos - 2sin 2 = 0;

2sin (cos - sin ) = 0.

2sin = 0 или cos - sin = 0.

1) 2sin = 0; = πn; x = 2πn, n є Z.

2) cos = sin ; tg = 1, = + πk; x = + 2πk, k є Z.

Ответ. x = 2πn, n є Z; x = + 2πk, k є Z.

7) Применение основного тригонометрического тождества.

Пример. sin x + cos x = 1.

Из тождества sin 2 x + cos 2 x = 1 имеем cos 2 x = 1 - sin 2 x, откуда

cos x = ± . 

sin x ± = 1; ± = 1 – sin x; 1 - sin 2 x = (1 – sin x) 2 ;

(1- sin x) (1 + sin x) - (1 – sin x) 2 = 0; (1- sin x) (1 + sin x – 1 + sin x) = 0;

(1 - sin x) ∙ 2sin x = 0.

1 – sin x = 0 или 2 sin x = 0.

1) sin x = 1; x = + 2πk, k є Z.

Корни необходимо проверить.

При х = + 2πn, n є Z, 1+ 0 = 1 верно.

х = + 2πn, n є Z – корни уравнения.

2) sin x = 0; x = πn, n є Z.

Корни необходимо проверить.

При х = 0 + 2πn, n є Z, 0 + 1 = 1 верно.

х = 2πn, n є Z – корни уравнения.

При х = π + 2πn, n є Z, 0 - 1 = 1 неверно.

х = π + 2πn, n є Z – не являются корнями уравнения.

Ответ. x = 2πn, n є Z; x = + 2πk, k є Z

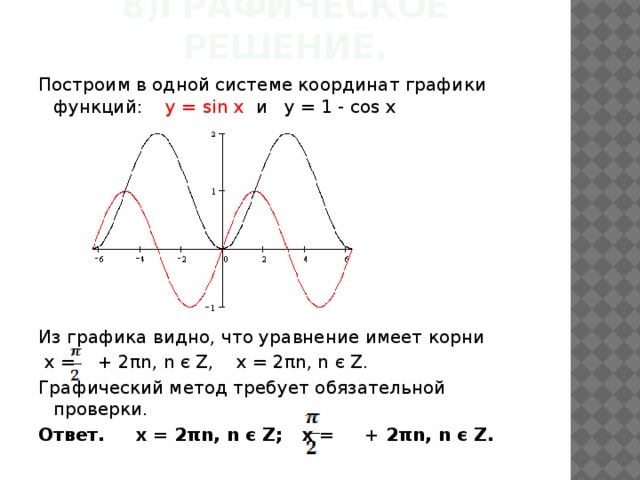
8)Графическое решение.

Построим в одной системе координат графики функций: y = sin x и y = 1 - cos x

Из графика видно, что уравнение имеет корни

х = + 2πn, n є Z, х = 2πn, n є Z.

Графический метод требует обязательной проверки.

Ответ. x = 2πn, n є Z; x = + 2πn, n є Z.