Презентация по математике по теме "Функции и их графики"

АННОТАЦИЯ

Проект разработан с использованием ИКТ и элементами модульной педагогической технологии. Он может быть проведен с учащимися 7-9 классов. Проект охватывает изучение тем: «Что такое функция?», «Графики функций», «Прямая пропорциональность и ее график», «Линейная функция и ее график», «Обратная пропорциональность и ее график».

Основная цель- создать такую систему, которая бы обеспечивала бы образовательные потребности каждого ученика в соответствии с его склонностями, интересами и возможностями.

Данный проект формирует понятия функции, график функции, способы построения графиков функций, способствует развитию учащихся творческого подхода к решению задач на построение графиков функций, на нахождение области определения функции и области значения функции, позволяет выработать навыки с информацией из разных источников, используя разнее формы исследования.

При проведении проекта с опорой на формирующее оценивание учитель помогает ученикам в развитии их навыков решение задач с использованием графиков, организует самостоятельные исследования по учебной теме.

План оценивания в ходе проекта направлен на реализацию деятельного подхода в обучении, в центре внимания учебные потребности ребенка, развитие навыков самоуправления обучением, самооценивание, взаимное оценивание.

Цели

- изучив этот проект, учащиеся должны:

- знать: основные функциональные понятия: понятие « функция», «график функции», «аргумент», «значение функции», « область определения функции», « область значений функции», «прямая пропорциональность и ее график», « коэффициент», как влияет знак коэффициента на расположение в координатной плоскости графиков функций прямой и обратной пропорциональностей ; понятие « линейной функции», что является графиком линейной функции, способы построения графиков линейных функций; « обратная пропорциональность и ее график»; дополнительно рассмотреть построение графика функции с модулем.

- Уметь: выполнять построение графиков: прямой пропорциональности; линейной функции (различными способами), обратной пропорциональности и графики функций с модулем; находить по графику значение функции по известному значению аргумента и решать обратную задачу; определять взаимное расположение графиков линейных функций в зависимости от коэффициента k и числа в; в каких координатных четвертях расположен график обратной пропорциональности; производить самооценку и взаимооценку, рефлексию деятельности.

Полную информацию смотрите в файле. 

7 КЛАСС. АЛГЕБРА.

ПРОЕКТ ПО МАТЕМАТИКЕ ТЕМА: «ФУНКЦИИ И ИХ ГРАФИКИ».

Инструкция. Презентация выполнена с помощью управляющих кнопок. Работу можно использовать для демонстрации в классе, а также использовать в компьютерном классе.

ЛИНЕЙНАЯ ФУНКЦИЯ У=КХ+В И ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ У=К/Х.

АННОТАЦИЯ

Проект разработан с использованием ИКТ и элементами модульной педагогической технологии. Он может быть проведен с учащимися 7-9 классов. Проект охватывает изучение тем: «Что такое функция?», «Графики функций», «Прямая пропорциональность и ее график», «Линейная функция и ее график», «Обратная пропорциональность и ее график».

Основная цель- создать такую систему, которая бы обеспечивала бы образовательные потребности каждого ученика в соответствии с его склонностями, интересами и возможностями.

Данный проект формирует понятия функции, график функции, способы построения графиков функций, способствует развитию учащихся творческого подхода к решению задач на построение графиков функций, на нахождение области определения функции и области значения функции, позволяет выработать навыки с информацией из разных источников, используя разнее формы исследования.

При проведении проекта с опорой на формирующее оценивание учитель помогает ученикам в развитии их навыков решение задач с использованием графиков, организует самостоятельные исследования по учебной теме.

План оценивания в ходе проекта направлен на реализацию деятельного подхода в обучении, в центре внимания учебные потребности ребенка, развитие навыков самоуправления обучением, самооценивание, взаимное оценивание.

План

• Аннотация.
• Цели.
• Ожидаемые результаты.
• Учебные вопросы.
• Теоретический материал.
• Проверочные работы.
• Критерии оценивания.
• Литература.

Цели

• изучив этот проект, учащиеся должны:
• -знать: основные функциональные понятия: понятие « функция», «график функции», «аргумент», «значение функции», « область определения функции», « область значений функции», «прямая пропорциональность и ее график», « коэффициент», как влияет знак коэффициента на расположение в координатной плоскости графиков функций прямой и обратной пропорциональностей ; понятие « линейной функции», что является графиком линейной функции, способы построения графиков линейных функций; « обратная пропорциональность и ее график»; дополнительно рассмотреть построение графика функции с модулем.
• Уметь: выполнять построение графиков: прямой пропорциональности; линейной функции (различными способами), обратной пропорциональности и графики функций с модулем; находить по графику значение функции по известному значению аргумента и решать обратную задачу; определять взаимное расположение графиков линейных функций в зависимости от коэффициента k и числа в; в каких координатных четвертях расположен график обратной пропорциональности; производить самооценку и взаимооценку , рефлексию деятельности.

Ожидаемые результаты обучения

• После завершения проекта учащиеся смогут:
• - назвать как минимум: что такое функция, график функции, область определения функции, область значений функции, аргумент, значение функции, угловой коэффициент;
• - виды функций: прямая пропорциональность, линейная функция, обратная пропорциональность; какими формулами они задаются и, что является их графиками;
• - перечислить способы построения графиков;
• - выполнять построение графиков;
• - решать задачи на построение графиков данных функций;
• - находить область определения функций, область значений функций;
• - называть аргумент, значение функции;
• - определять угловой коэффициент и что он показывает;
• - распределять обязанности в группе при работе над общей задачей;
• - приобрести новые учебные навыки;
• - продемонстрировать итоговый продукт работы группы или индивидуальный.

Учебные вопросы

• - Что такое функция?
• (Зависимость одной переменной от другой называют функциональной зависимостью или функцией).
• - Что называется аргументом?
• ( Независимую переменную называют аргументом).
• - Что называется значением функции?
• (Значение зависимой переменной называется значением функции).
• - Что является областью определения функции?
• (Все значения, которые принимает независимая переменная, образуют область определения функции).
• - Что является областью значений функции?
• (Все значения, которые принимает зависимая переменная, образуют область значений функции).
• - Что такое график функции?
• (Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции).

0, то прямая расположена в I и III координатных четвертях, а если к(презентация) - Какая функция называется линейной? - Что является графиком линейной функции? - Способы построения графика линейной функции. - Что такое обратная пропорциональность? - Что является графиком обратной пропорциональности? - Как построить график обратной пропорциональности? " width="640"

• -Что такое прямая пропорциональность?
• (Прямой пропорциональностью называется функция, которую можно задать формулой вида у = кх, где х- независимая переменная, к- не равное нулю число).
• - Что является графиком прямой пропорциональности?
• (График прямой пропорциональности представляет собой прямую, проходящую через начало координат).
• - Что такое число к? Что оно показывает?
• (к- угловой коэффициент. Число к показывает как расположен график прямой пропорциональности. Если к0, то прямая расположена в I и III координатных четвертях, а если к
• (презентация)
• - Какая функция называется линейной?
• - Что является графиком линейной функции?
• - Способы построения графика линейной функции.
• - Что такое обратная пропорциональность?
• - Что является графиком обратной пропорциональности?
• - Как построить график обратной пропорциональности?

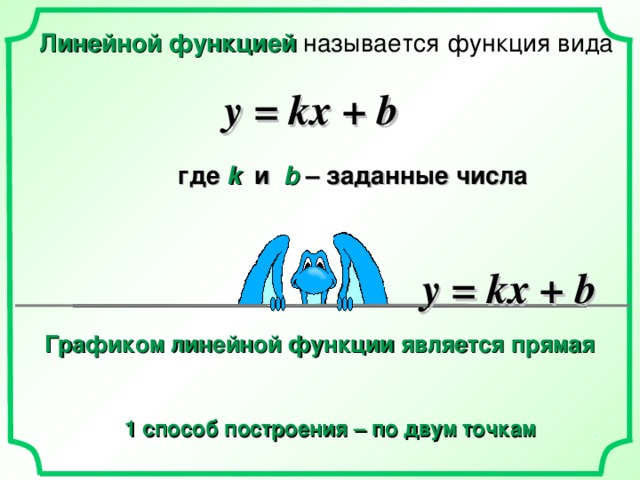
Линейной функцией называется функция вида

у = kx + b

где k и b – заданные числа

у = kx + b

Графиком линейной функции является прямая

1 способ построения – по двум точкам

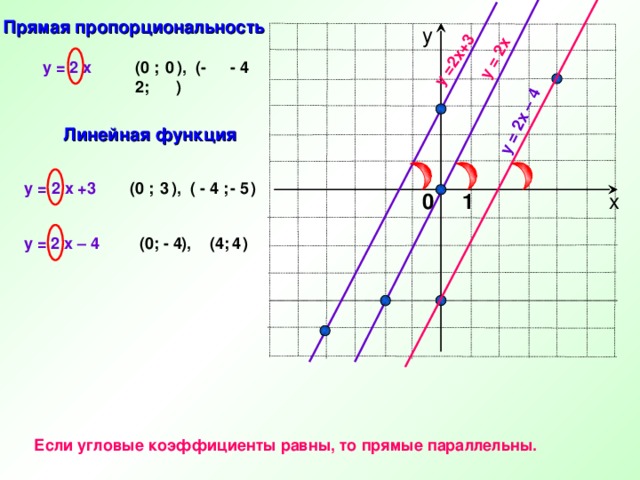
y = 2x

y = 2 x+3

y = 2x – 4

Прямая пропорциональность

у

y = 2 x

- 4

(0 ; ), (- 2; )

0

Линейная функция

(0 ; ), ( - 4 ; )

y = 2 x +3

3

- 5

1

х

0

(0; ), (4; )

y = 2 x – 4

- 4

4

Если угловые коэффициенты равны, то прямые параллельны.

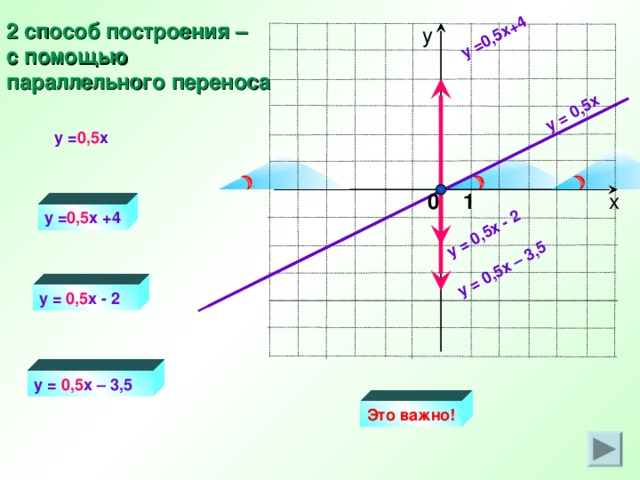
y = 0,5x

y = 0,5 x+4

y = 0,5x - 2

y = 0,5x – 3,5

2 способ построения –

с помощью

параллельного переноса

у

y = 0,5 x

х

0 1

y = 0,5 x +4

y = 0,5 x - 2

y = 0,5 x – 3,5

Это важно!

0 х 0 1 b 0 " width="640"

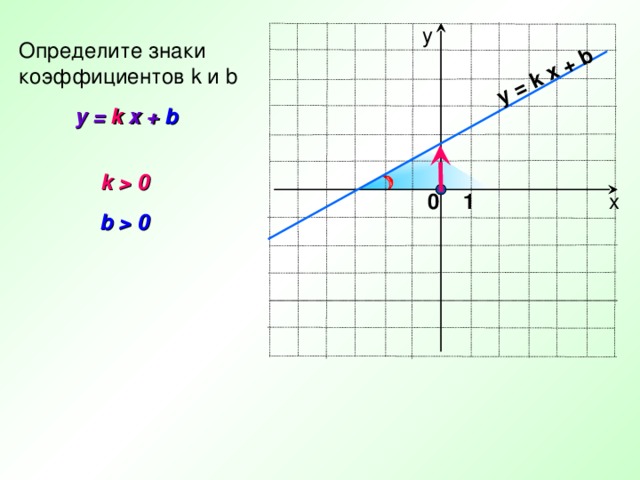
y = k x + b

у

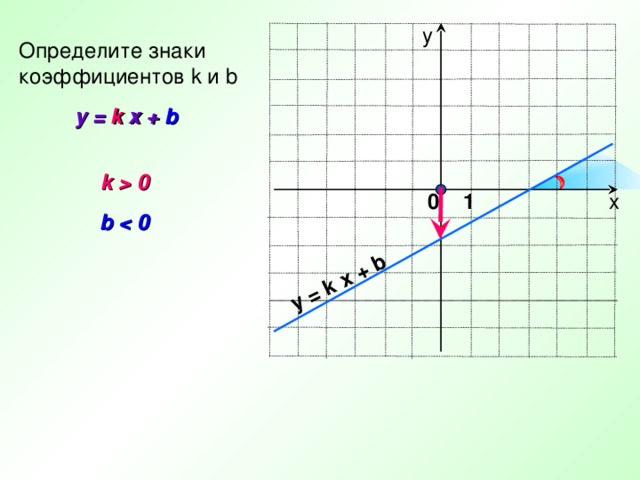
Определите знаки

коэффициентов k и b

y = k x + b

k 0

х

0 1

b 0

0 х 0 1 b " width="640"

y = k x + b

у

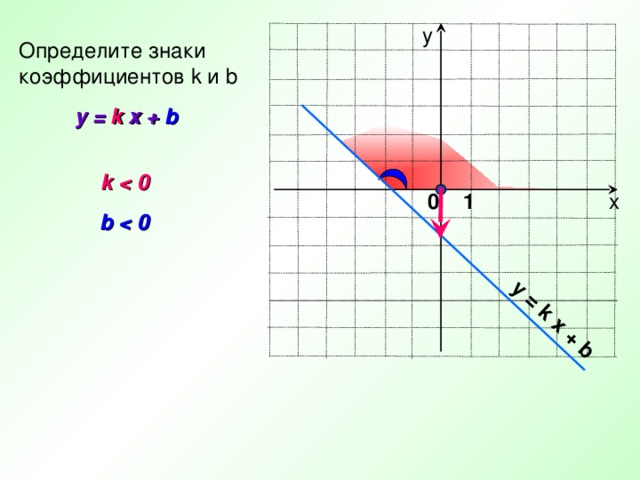
Определите знаки

коэффициентов k и b

y = k x + b

k 0

х

0 1

b

y = k x + b

у

Определите знаки

коэффициентов k и b

y = k x + b

k

х

0 1

b

0 " width="640"

y = k x + b

у

Определите знаки

коэффициентов k и b

y = k x + b

k

х

0 1

b 0

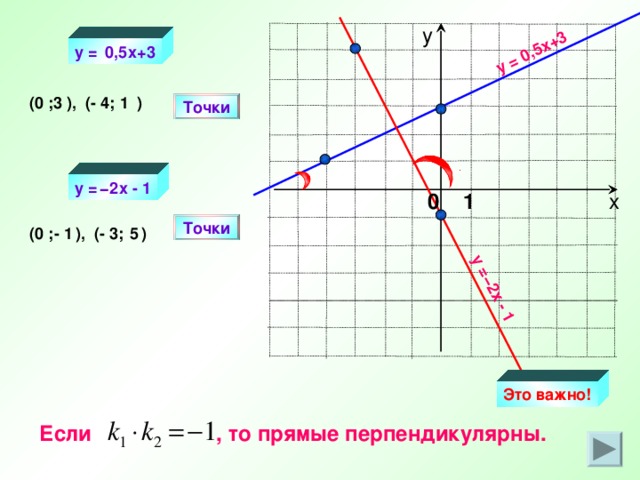
y = 0,5x+3

y = − 2х - 1

у

y = x+3

0,5

3

(0 ; ), (- 4; )

1

Точки

− 2

y = х - 1

0 1

х

Точки

(0 ; ), (- 3; )

- 1

5

Это важно!

Если , то прямые перпендикулярны.

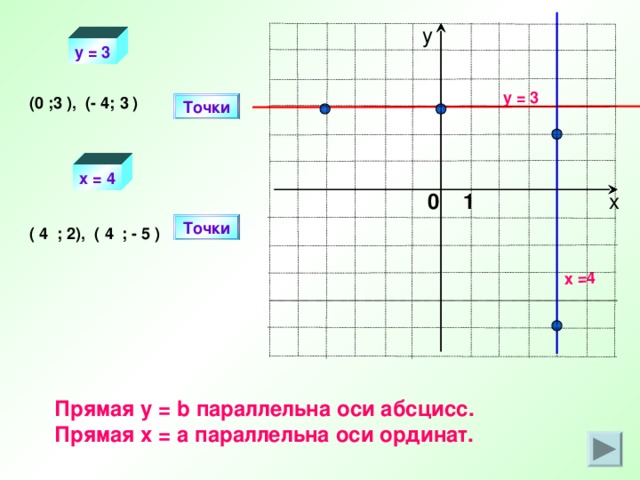
x = 4

у

y = 3

y = 3

(0 ; ), (- 4; )

3

3

Точки

x = 4

х

0 1

Точки

4

4

( ; 2), ( ; - 5 )

Прямая y = b параллельна оси абсцисс.

Прямая х = а параллельна оси ординат.

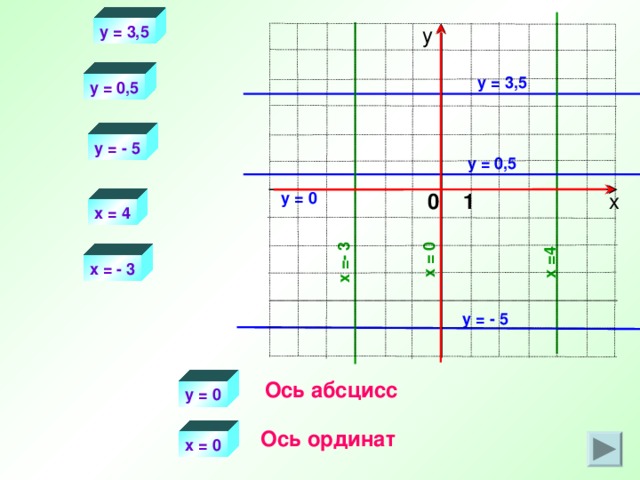
x = 4

x = - 3

x = 0

y = 3,5

у

y = 3,5

y = 0,5

y = - 5

y = 0,5

х

0 1

y = 0

x = 4

x = - 3

y = - 5

Ось абсцисс

у = 0

Ось ординат

х = 0

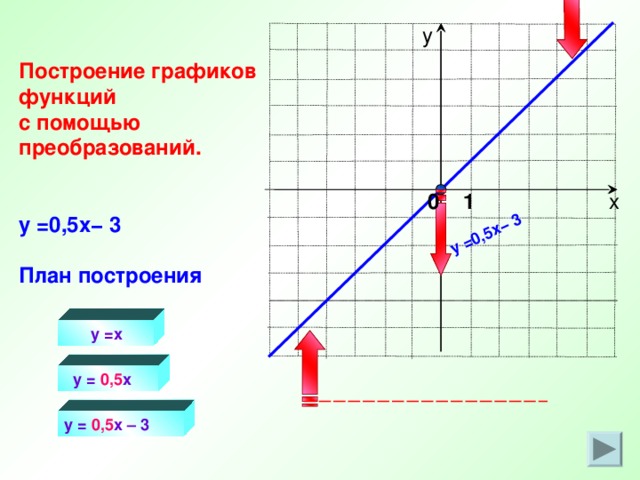
y =0,5x− 3

у

Построение графиков функций

с помощью преобразований.

y = 0,5 x − 3

План построения

х

0 1

y =x

y = 0,5 x

y = 0,5 x – 3

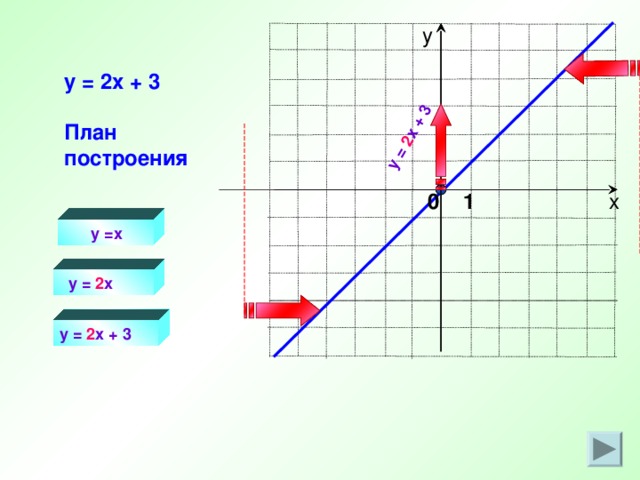
y = 2 x + 3

у

y = 2 x + 3

План построения

х

0 1

y =x

y = 2 x

y = 2 x + 3

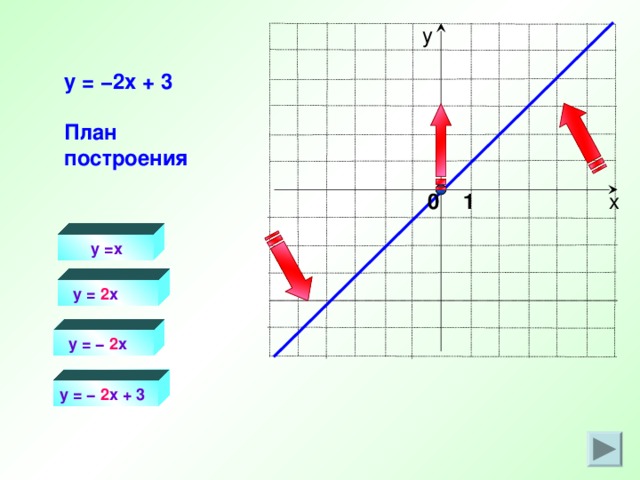
у

y = −2 x + 3

План построения

0 1

х

y =x

y = 2 x

y = − 2 x

y = − 2 x + 3

Проверочная работа №1

• Постройте график линейной функции:
• а) у=х+5; з) у=4; и) у=-3;
• б) у=-0,5х; к)у=2,5; л) у=-1.5;
• в) у=-2х-6; м) х=3: н) х=-2;
• г) у=0,3х-6; о) х=3,5 п) х=-4,5.
• е) у=5х-2;
• ж) у=-2/3*х
• Используя график у=3х-4,определите:
• а) чему равно значение функции при значении аргумента, равном 1; -1; 0; 2
• б) при каком значении аргумента значение функции равно 3; -1; 0; -2.
• Проверьте результаты вычислением.
• Постройте в одной системе координат графики функций и укажите координаты точки их пересечения:
• а) у=0,5х-1 и у=-х-4;
• б) у=5-х и у=х-5.

• Постройте график функции, заданной следующим условием:
• а) значения у равны 1 при всех неположительных значениях х и равны -3 при всех положительных значениях х. значения у равны 4 при всех неотрицательных значениях х.
• б) значения у равны 4 при всех неотрицательных значениях х и равны -4 при всех отрицательных значениях х.
• Задайте формулой линейную функцию, если известны угловой коэффициент k соответствующей прямой и координаты точки А через которую она проходит:
• а) k=2/5, А(-10;-4); б) k=-3, А(3;8).
• Постройте прямую, если ее угловой коэффициент равен 0,5 и она проходит через точку (4;-2). Задайте формулой линейную функцию график которой параллелен указанной прямой и пересекает ось у в точке (0;1).

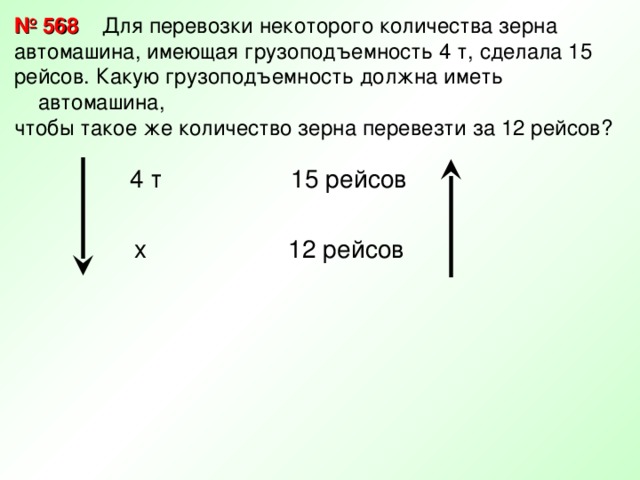
№ 568 Для перевозки некоторого количества зерна

автомашина, имеющая грузоподъемность 4 т, сделала 15

рейсов. Какую грузоподъемность должна иметь автомашина,

чтобы такое же количество зерна перевезти за 12 рейсов?

15 рейсов

4 т

х

12 рейсов

23

Поезд движется из Москвы в Санкт-Петербург со скоростью v км/ч. За какое время поезд пройдет путь 700 км?

700

t =

v

Москва

700

t ( v ) =

Санкт-Петербург

v

24

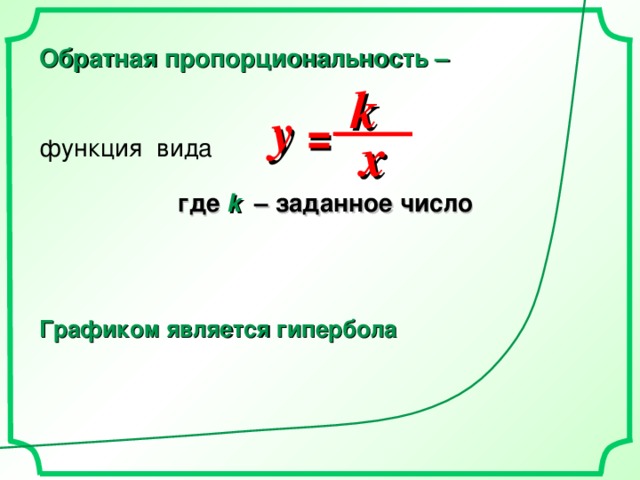
Обратная пропорциональность –

функция вида

где k – заданное число

k

y =

x

Графиком является гипербола

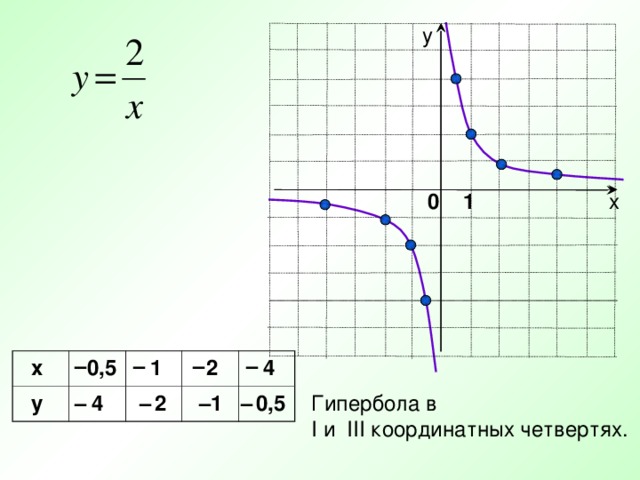
у

х

0 1

– – – –

х

у

0,5

1

2

4

4

Гипербола в

I и III координатных четвертях.

1

2

0,5

– – – –

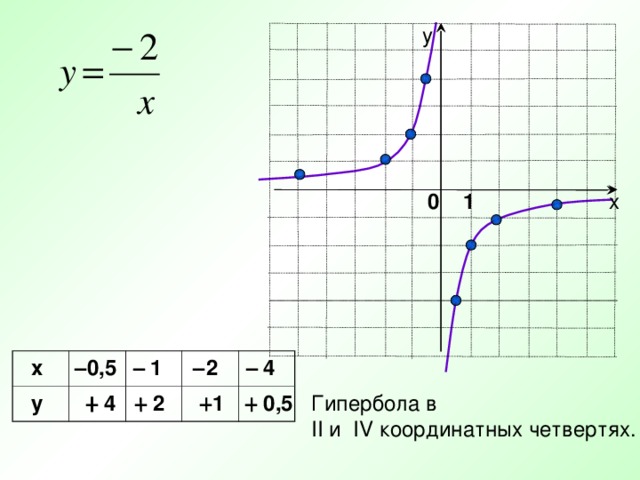
у

х

0 1

– – – –

х

у

0,5

1

2

4

– 4

Гипербола в

II и IV координатных четвертях.

– 2

– 1

– 0,5

Проверочная работа №2

• Постройте график функции:
• а) у= 4/х;
• б) у=-4/х;
• в) у=8/х;
• г) у=-8/х.
• Постройте график функции у=9/х. Найдите:
• а) значение функции, соответствующее значению аргумента, равному --5; -2; 2;5.
• б) значение аргумента, которому соответствует значение функции, равное -9; -2,3; 2,3; 9.
• в) при каких значениях аргумента значение функции больше 0; меньше 0.
• Принадлежит ли графику функции у=-128/х точка: А(-4;32), В(8;-16),
• С(2;64), Д(0;-128)?
• Сколько точек, у которых абсцисса равна ординате, имеет график функции у=49/х? Найдите координаты всех таких точек.
• Прямоугольник со сторонами а см и в см имеет площадь 18 кв. см. Задайте формулой зависимость в от а и постройте график этой функции.
• Постройте график функции:
• а) у=-6/|х|;
• б)у=2|х|.

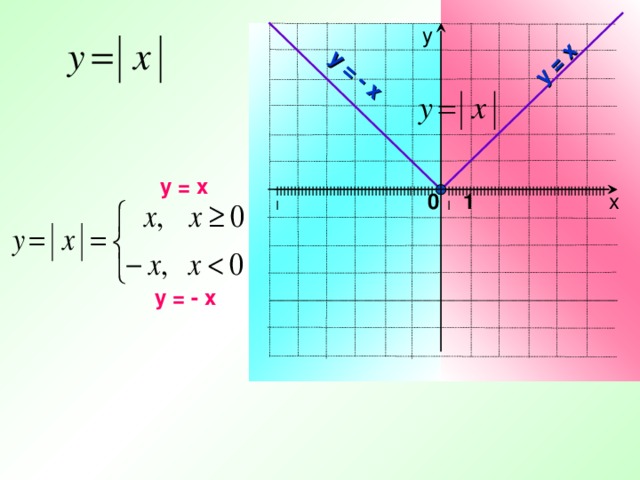
у = х

у = - х

у

у = х

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

х

0 1

у = - х

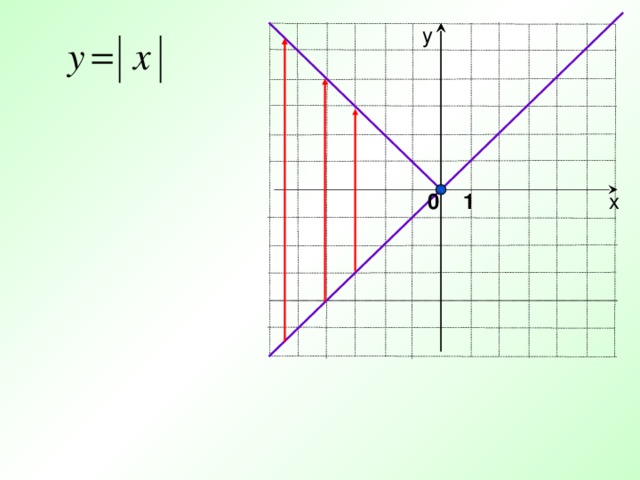
у

х

0 1

Проверочная работа №3

• Построить график функции:
• а) у=|х|;
• б) у=|х| + з;
• в) у= -|х| ;
• г) у=-|х| + 4;
• д) у=-|х|-2;
• е) у=х+2|
• ж) у=|х-3|;
• з) у=-|х+5| -7;
• и) у=|х-1| + 2.
• Построить в одной системе координат графики функций и найдите координаты точек пересечения, если таковы имеются:
• а) у=2х, у=-2х+3;
• б) у=-3х+4, у=-3х-4;
• в) у=-х+5, у=6/х;
• г) у=-4х+1, у=-12/х;
• д) у=8/х, у=-4/х;
• е) у=6/х, у=9/х;
• ж) у=х+4, у=10/х; у=|х|;
• з) у= 3х-1, у=4/х, у=-|х|+2.

Критерии оценивания

• Формы оценивания:
• промежуточное (формирующее) оценивание:
• - самооценка, взаимооценка участников проекта своей деятельности для выявления потребности в необходимой или дополнительной информации; процесса в понимании теоретического материала.
• СПОСОБЫ ОЦЕНИВАНИЯ : тесты, проверочные работы, самостоятельные работы, подготовленные учителем и соответствующие учебной программе и стандарту (Раздаточный материал, дидактический материал).
• Итоговое оценивание:
• - оценка содержания итогового материала, его соответствие стандарту и учебной программе;
• - оценка навыков совместной деятельности (групповой) и индивидуальной;
• - оценка навыков мышления (достигнута цель).

Литература

• 1 .Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б.Суворов.
• Под род. С.А. Теляковского. Алгебра: Учебник для 7 класса.-18 изд.- М: Просвещение,2009.
• 2.Ю.Н Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов. Под ред. С.А. Теляковского. Алгебра: Учебник для 8 класса- изд.- М:Просвещение,2010.
• 3.Звавич Л.П., Кузнецова Л. В., Суворова С.Б. Дидактические материалы по алгебре для 7 класса.-14изд.- М.: Просвещение, 2009.
• 4.Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г. Дидиктические материалы по алгебре для 8 класса.- 15изд.- М.: Просвещение, 2010.
• 5.Руркин А.Н., Лупенко Г.В., Масленникова И.А. Поурочные разработки по алгебре: 7 класс,- М.: ВАКО, 2009.
• 6.Т.М. Ерина. Поурочное планирование по алгебре. 7класс: к учебнику Ю.Н. Макарычева и др.- 3 изд. 2011.
• 7. WWW.mathtematir.ru
• 8 .htt:// jetopisi isi .ru/ index.php/
• 9. Mathgia.ru
• 10. School- collection.edu