
«Мне приходится делить время между политикой и уравнениями. Однако , уравнения ,по-моему, гораздо важнее. Политика существует для данного момента, а уравнения будут существовать вечно»
Альберт Энштейн

ГАОУ СПО НСО «Барабинский медицинский колледж»
РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Алгебра и начала анализа.
Преподаватель математики: Вашурина Т. В.
Барабинск, 2015

Цели урока:
- Рассмотреть понятие иррационального уравнения, различные способы решения иррациональных уравнений.
- Формировать умение решать простейшие иррациональные уравнения, проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени.

Математический диктант
- Корень -й степени из числа а -
- Корень -й степени из числа а -

Математический диктант
- Если n – четно, a , то …
- Если n – четно, a , то …

Математический диктант
- Арифметическим корнем n –ой степени называется…
- Арифметическим корнем n –ой степени называется…

Математический диктант
- Запишите все известные вам свойства корня n –ой степени
- Запишите все известные вам свойства корня n –ой степени

Математический диктант (взаимопроверка)
1. Корень -й степени из числа - это число, -я степень которого равна .)
2. Если n – четно, a
3. Арифметическим корнем n –ой степени называется неотрицательное число, n –я степень которого равна а)
4. Если n – нечетно, то тогда уравнение имеет единственный корень при любом .
5. Запишите все известные вам свойства корня n –ой степени
1.
2.
3.
4.
5.

Критерии оценок:
- «5» баллов – 5 верных ответов и формул
- «4» балла – 4 верных ответов и формул
- «3» балла – 3 верных ответов и формул

Алгоритм решения иррациональных уравнений методом возведения в степень, равную степени корня.
1.Возведём обе части уравнения в степень , равную степени корня.
2. Решим полученное уравнение.
3. Выполним проверку.

Метод пристального взгляда
- Этот метод основан на следующем теоретическом положении: “Если функция возрастает в области определения и число входит в множество значений, то уравнение имеет единственное решение.”
- Для реализации метода, основанного на этом утверждении требуется:
- а) Выделить функцию, которая фигурирует в уравнении.
- b) Записать область определения данной функции.
- c) Доказать ее монотонность в области определения.
- d) Угадать корень уравнения.
- t) Обосновать, что других корней нет.
- f) Записать ответ.

Решение уравнений с использованием замены переменной.
- Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение радикал. При этом уравнение становится рациональным относительно новой переменной.

Первичное закрепление знаний
учебник Алгебра и начала математического анализа. Под ред. А. Н. Колмагорова: стр. 216 №417, 419

Решение упражнений
- Учебник Алгебра и начала математического анализа. Под ред. А. Н. Колмагорова:
216 №420 (а,г), 421 (б,в)

Самостоятельная работа

Выполнение задания для итогового контроля
- . (Учебник для общеобразовательных учреждений
- Алгебра и начала математического анализа. Под ред. А. Н. Колмагорова: стр. стр.216 №420 (б,в), 421 (а,г))
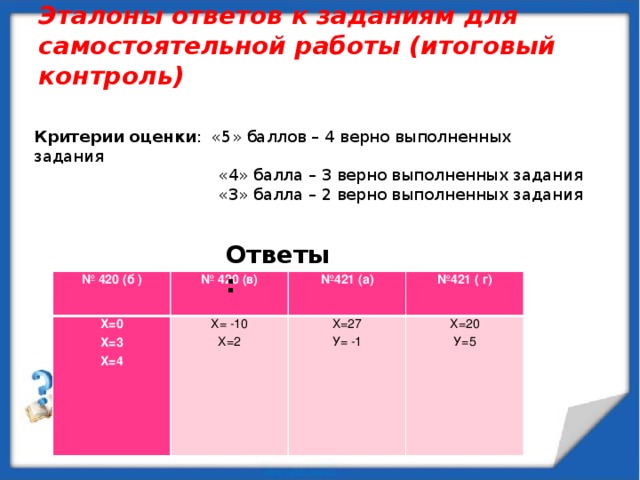
Эталоны ответов к заданиям для самостоятельной работы (итоговый контроль)
Критерии оценки : «5» баллов – 4 верно выполненных задания
«4» балла – 3 верно выполненных задания
«3» балла – 2 верно выполненных задания
Ответы:
№ 420 (б )
Х=0
№ 420 (в)
№ 421 (а)
Х=3
Х= -10
№ 421 ( г)
Х=4
Х=27
Х=2
Х=20
У= -1
У=5

Домашнее задание
- На оценку «3»: . Учебник Алгебра и начала математического анализа. Под ред. А. Н. Колмагорова, 10-11 классы: с. 214-216, упр. 418, (работа с приложением на электронном носителе ), конспект учить.
- На оценку «4»: Учебник Алгебра и начала математического анализа. Под ред. А. Н. Колмагорова, 10-11 классы: с. 214-216, упр. 418, 422 (а), (работа с приложением на электронном носителе ), конспект учить.
- На оценку «5»: Учебник Алгебра и начала математического анализа. Под ред. А. Н. Колмагорова, 10-11 классы: с. 214-216, упр. 418, 422(б, в), (работа с приложением на электронном носителе ), конспект учить.

Да , мир познания не сладок,
И знаем мы со школьных лет,
Загадок больше , чем разгадок,
И поискам предела нет!

Спасибо за урок!


 Получите свидетельство
Получите свидетельство Вход
Вход
































 Презентация по математике на тему: "Решение иррациональных уравнений" (0.32 MB)
Презентация по математике на тему: "Решение иррациональных уравнений" (0.32 MB)
 0
0 565
565 63
63 Нравится
0
Нравится
0


