Презентация по математике "Метод интервалов"

Решение неравенства.

Решением неравенства с неизвестным х называют число, при подстановке которого в это неравенство вместо х получается верное числовое неравенство.

Решить неравенство – значит найти все его решения или показать, что их нет.

Рассмотрим способ решения неравенств вида:

(х - х₁) (х - х₂)· … · (х - х_n) > 0 и (х - х₁) (х - х₂)· … · (х - х_n) < 0, где х₁ < х₂ < … < х_n , n – натуральное число (n ≥1).

Пусть требуется решить неравенство:

(х - х₁) (х - х₂)(х – х₃) > 0

Или неравенство

(х - х₁) (х - х₂)(х – х₃) < 0, где х₁ < х₂ < х₃

Рассмотрим многочлен

А(х) = (х - х₁) (х - х₂)(х – х₃)

1. А(х)>0, при  x ϵ  (x₁ ;x₂)U(x₃;+∞)

Весь материал - смотрите документ.

x 1

x 3

+

+

x 2

-

-

x

Решение неравенства

• Решением неравенства с неизвестным х называют число, при подстановке которого в это неравенство вместо х получается верное числовое неравенство.
• Решить неравенство – значит найти все его решения или показать, что их нет.

0 и (х - х 1 ) (х - х 2 ) · … · (х - х n ) где х 1 х 2 … х n , n – натуральное число ( n ≥ 1 ). " width="640"

Рассмотрим способ решения неравенств вида:

(х - х 1 ) (х - х 2 ) · … · (х - х n ) 0

и

(х - х 1 ) (х - х 2 ) · … · (х - х n )

где

х 1 х 2 … х n , n – натуральное число

( n ≥ 1 ).

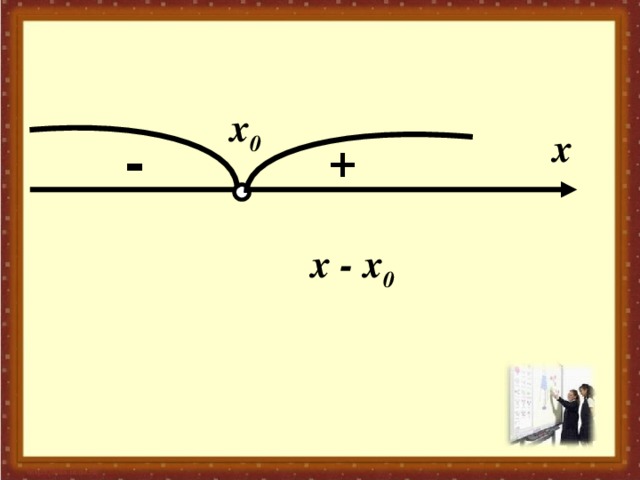
x 0

x

-

+

х - x 0

0 Или неравенство (х - х 1 ) (х - х 2 )(х – х 3 ) где х 1 х 2 х 3 x 1 x 3 x 2 x (- ∞ ; x 1 ) ( x 1 ; x 2 ) ( x 2 ; x 3 ) ( x 3 ;+ ∞ ) " width="640"

Пусть требуется решить неравенство:

(х - х 1 ) (х - х 2 )(х – х 3 ) 0

Или неравенство

(х - х 1 ) (х - х 2 )(х – х 3 ) где х 1 х 2 х 3

x 1

x 3

x 2

x

(- ∞ ; x 1 ) ( x 1 ; x 2 ) ( x 2 ; x 3 ) ( x 3 ;+ ∞ )

0 , при x ϵ ( x 1 ; x 2 ) U ( x 3 ;+ ∞ ) 2. А(х) ,при x ϵ (- ∞ ; x 1 ) U ( x 2 ; x 3 ) " width="640"

Рассмотрим многочлен А(х) = (х - х 1 ) (х - х 2 )(х – х 3 )

x 3

x 1

x 1

x 3

x 2

x 2

x

x

+

-

-

+

1. А(х) 0 , при x ϵ ( x 1 ; x 2 ) U ( x 3 ;+ ∞ )

2. А(х) ,при x ϵ (- ∞ ; x 1 ) U ( x 2 ; x 3 )

0 (х - х 1 ) (х - х 2 ) · … · (х - х n ) 0 x ϵ ( x 1 ; x 2 ) U ( x 3 ;+∞) x ϵ (-∞; x 1 ) U ( x 2 ; x 3 ) 19.12.16 6 " width="640"

Метод интервалов

x 1

x 3

x 2

x

+

-

-

+

• На оси абсцисс отмечают точки х 1 ;х 2 ;х 3 ;
• Над интервалом (х 3 ;+∞) ставят знак «+»
• Над интервалом (х 2 ;х 3 ) ставят знак «-»
• Над интервалом (х 1 ;х 2 ) ставят знак «+»
• Над интервалом (-∞;х 1 ) ставят знак «-»
• Решение неравенства

(х - х 1 ) (х - х 2 ) · … · (х - х n ) 0

(х - х 1 ) (х - х 2 ) · … · (х - х n ) 0

x ϵ ( x 1 ; x 2 ) U ( x 3 ;+∞)

x ϵ (-∞; x 1 ) U ( x 2 ; x 3 )

19.12.16

6

0 . Отметим на оси ОХ точки 2;3;4 Над интервалами(4;+∞);(3;4);(2;3);(-∞;2) справа налево поставим поочередно знаки «+»; «-». Ответ:(2;3) U (4; +∞) - 2 4 3 - + x + " width="640"

Пример 1

• Решим неравенство: (х-2)(х-3)(х-4) 0 .
• Отметим на оси ОХ точки 2;3;4
• Над интервалами(4;+∞);(3;4);(2;3);(-∞;2) справа налево поставим поочередно знаки «+»; «-».
• Ответ:(2;3) U (4; +∞)

-

2

4

3

-

+

x

+

0 Разложим квадратный трехчлен на множители:(2-х)(х-3)(х-1)(х+1) 0 умножим обе части неравенства на -1 (х-(-1))(х-1)(х-2)(х-3) Отметим на оси ОХ точки-1;1;2;3 Ответ:(-1;1) U (2;3) + 3 1 + - 2 + -1 - x " width="640"

Пример 2

• Решим неравенство: (2-х)(х 2 -4х+3)(х+1) 0

• Разложим квадратный трехчлен на множители:(2-х)(х-3)(х-1)(х+1) 0
• умножим обе части неравенства на -1
• (х-(-1))(х-1)(х-2)(х-3)
• Отметим на оси ОХ точки-1;1;2;3
• Ответ:(-1;1) U (2;3)

+

3

1

+

-

2

+

-1

-

x

Пример3

• Решим неравенство:(х-1)(х-3)(х 2 +х+1)
• Трехчлен х 2 +х+1 принимает только положительные значения( D .
• Наше неравенство равносильно
• (х-1)(х-3)
• Решая методом интервалов получим
• Ответ:(1;3)

+

-

+

3

1

Пример 4

• Решим неравенство :(х-1) 3 (х-2) 2 (х-3) 4 (х-4)

• Для решения таких неравенств используют общий метод интервалов , он состоит в следующем:
• Отметим на оси ОХ точки 1;2;3;4, а затем в каждом интервале исследуем знак многочлена А(х)= (х-1) 3 (х-2) 2 (х-3) 4 (х-4)
• Ответ:(1;2) U (2;3) U (3;4).

2

4

3

-

-

+

-

1

x

+