Презентация по информатике «Системы счисления»

Цель:

- Дать представление о понятии система счисления.

- Познакомить с различными СС (позиционными и непозиционными).

- Сформировать начальный навык работы в традиционных позиционных СС.

Основные понятия.

Опр: Система счисления -  это комплекс правил наименования и записи чисел.

Число в математике и информатике - это величина, а не символьная запись.

Опр: Цифры – это символы, с помощью которых в данной системе счисления записываются все числа.

Опр: Алфавит – совокупность различных цифр, используемых для записи чисел.

Системы счисления:

- позиционные

352, 23

величина числа зависит от  номера позиции цифры при его записи.

- непозиционные

VII, XIX

каждой цифре соответствует величина, не зависящая  от ее места в записи числа.

Непозиционные системы счисления.

Пример: римская система счисления.

В качестве цифр используются некоторые буквы.

Значение цифры не зависит от ее положения в числе, например:

ХХХ = 10 + 10 + 10 = 30.

СИСТЕМЫ СЧИСЛЕНИЯ

Цель

• Дать представление о понятии система счисления
• Познакомить с различными СС (позиционными и непозиционными)
• Сформировать начальный навык работы в традиционных позиционных СС

Требования:

Изучить материал лекции

письменно ответить на вопросы

Основные понятия

Опр: Система счисления - это комплекс правил наименования и записи чисел.

Число в математике и информатике - это величина, а не символьная запись.

Опр: Цифры – это символы, с помощью которых в данной системе счисления записываются все числа.

Опр: Алфавит – совокупность различных цифр, используемых для записи чисел.

Системы счисления:

позиционные непозиционные

352 , 23

VII, XIX

каждой цифре соответствует величина, не зависящая от ее места в записи числа

величина числа зависит от номера позиции цифры при его записи

Непозиционные системы счисления

Пример: РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ

Значение цифры не зависит от ее положения в числе, например:

ХХХ = 10 + 10 + 10 = 30

В качестве цифр используются некоторые буквы.

I

1

V

X

5

L

10

C

50

100

D

M

500

1000

Величина числа в римской системе счисления определяется как сумма или разность чисел. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.

XXVIII = 10 + 10 + 5 + 1 + 1 + 1

XCIX = -10 + 100 – 1 + 10

Используя римскую систему счисления выпишите числа

от 95 до 105

100 =

101 =

95 =

102 =

9 6 =

103 =

9 7 =

104 =

9 8 =

105 =

9 9 =

непозиционные системы счисления

• Единичная («палочная»)

Период палеолита. 10-11 тысяч лет до н.э.

Древнеегипетская десятичная

непозиционная система

2,5 тысяч лет до н.э.

сотни

десятки

единицы

Позиционные

системы счисления

В позиционной системе счисления количественное значение цифры зависит от ее позиции в числе.

395 – здесь число «пять» показывает количество единиц

359 - здесь число «пять» показывает количество десятков

593 - здесь число «пять» показывает количество сотен

Позиционные

системы счисления

Опр: Количество цифр, которые используются в данной системе счисления, называется основанием данной системы счисления и обозначается буквой р .

В позиционной системе счисления количественное значение цифры зависит от ее позиции в числе.

Опр: Позиция цифры называется разрядом . Разряд числа возрастает справа налево.

2 1 0

542 нумерация разрядов

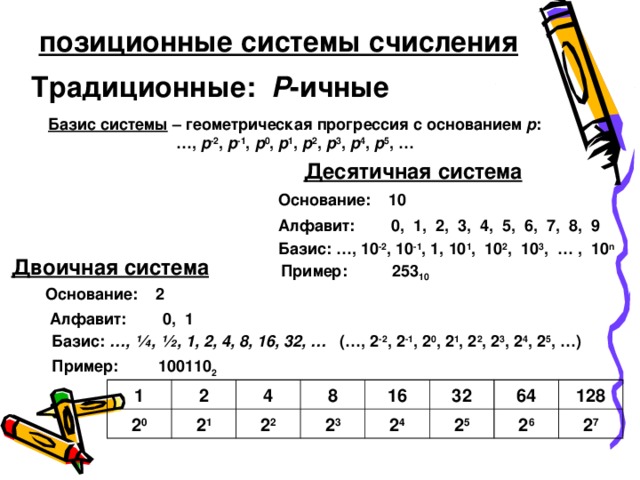
позиционные системы счисления

Традиционные: P -ичные

Базис системы – геометрическая прогрессия с основанием p :

… , p -2 , p -1 , p 0 , p 1 , p 2 , p 3 , p 4 , p 5 , …

Десятичная система

Основание: 10

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Базис: …, 10 -2 , 10 -1 , 1, 10 1 , 10 2 , 10 3 , … , 10 n

Двоичная система

Пример: 253 10

Основание: 2

Алфавит: 0, 1

Базис: …, ¼, ½, 1, 2, 4, 8, 16, 32, … (…, 2 -2 , 2 -1 , 2 0 , 2 1 , 2 2 , 2 3 , 2 4 , 2 5 , …)

Пример: 100110 2

1

2 0

2

4

2 1

8

2 2

16

2 3

32

2 4

64

2 5

128

2 6

2 7

В любой традиционной P -ичной позиционной системе счисления число равно сумме степеней основания:

147,205

14 7,205 10 = 1  10 0 + 4  10 + 7  1 + 2  0,1 + 0  0,01 + 5  0,001 =

= 1  10 2 + 4  10 1 +7  10 0 +2  10 -1 + 0  10 -2 + 5  10 -3

X p = a n …a 1 a 0 , b -1… b - k ... P

X = a n P n + a n-1 P n-1 + … + a 1 P + a 0 + b -1 P -1 + b -2 P -2 + … + b -k P -k + …

позиционные системы счисления

Нетрадиционные

Фибоначчиевая система

Базис: 1, 2, 3, 5, 8, 13, 21, 34, 55, …

Алфавит: 0, 1

Пример: 10000100 ф = 3 + 34 = 37 10

Смешанные: P-Q - ичные

Каждая цифра числа, заданного в Q - ичной системе,

заменяется ее представлением в P - ичной системе.

Двоично-десятичная система

35809 10 = 0011 0101 1000 0000 1001 2-10

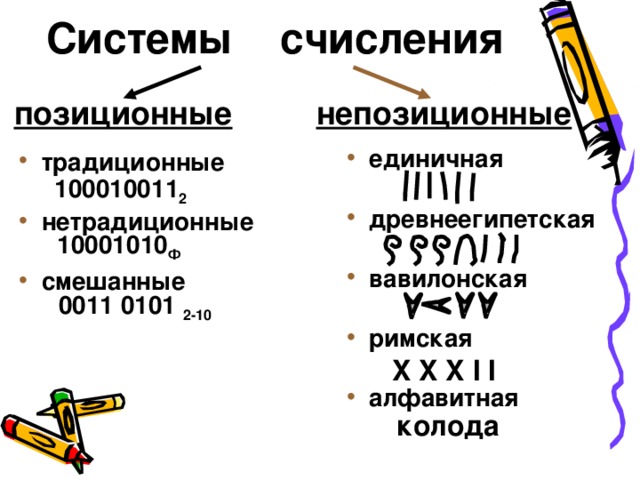
Системы счисления

позиционные

непозиционные

• единичная

• древнеегипетская

• вавилонская

• римская

• алфавитная

• традиционные

• нетрадиционные

• смешанные

100010011 2

10001010 Ф

0011 0101 2-10

X X X I I

колода

Домашнее задание

Выучить конспект

Изучить: ГЛАВА4.

Выполнить задание ОК №10, №11 (письменно).

(" Лекции по информатике 1 курс ")

( http://student.kmmt.ru/siklcom_KMT/inform_texn_2014/inform_1kurs_2014/ ).

на сайте КМТ ( http://www.kmmt.ru/ )