Презентация по информатике по теме "Основы логики"

НА УРОКЕ:

Что такое логика;

Основные формы мышления;

Базовые логические операции;

Логические выражения и таблицы истинности

Алгебра высказываний

В алгебре высказываний  суждениям ставятся в соответствие логические переменные. Истинному высказыванию соответствует значение логической переменной 1, а ложному – значение 0.

Основные логические операции

1. Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией

Полную информацию смотрите в файле. 

Основы логики

НА УРОКЕ:

• Что такое логика;
• Основные формы мышления;
• Базовые логические операции;
• Логические выражения и таблицы истинности

Логика – это наука о формах и способах мышления

Основные формы мышления

понятие

высказывание

умозаключение

Это форма мышления, фиксирующая основные, существенные признаки объекта.

Это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними.

Это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.

Алгебра высказываний

В алгебре высказываний суждениям ставятся в соответствие логические переменные. Истинному высказыванию соответствует значение логической переменной 1, а ложному – значение 0.

А=«Два умножить на два равно четырем» (А=1);

В=«Два умножить на два равно пяти»(В=0).

Основные логические операции

1. Объединение двух(или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией

F=A&B

А

0

В

F=A&B

0

0

1

0

1

1

0

0

0

1

1

«2*2=5 и 3*3=10»

«2*2=5 и 3*3=9»

«2*2=4 и 3*3=10»

«2*2=4 и 3*3=9»

Основные логические операции

2. Объединение двух(или нескольких) высказываний с помощью союза «или» называется операцией логического сложения или дизъюнкцией

F=A V B

А

0

В

F=A v B

0

0

1

0

1

1

0

1

1

1

1

«2*2=5 или 3*3=10»

«2*2=5 или 3*3=9»

«2*2=4 или 3*3=10»

«2*2=4 или 3*3=9»

Основные логические операции

3. Присоединение частицы «не» к высказыванию называется операцией отрицания или инверсией

_

F= А

А

0

F

1

1

0

«2*2 ≠4 »

«2*2=4»

Логические выражения и таблицы истинности

Каждое составное высказывание можно выразить в виде формулы в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции

(2*2=5 или 2*2=4) и (2*2 ≠5 или 2*2≠4 )

А = «2*2=5» - ложно (0)

В = «2*2=4» - истинно (1)

_

_

F=(A V B)&( A V B)

Таблица истинности логической функции

_

_

Заполнить таблицу истинности для логической функции:

F=(A V B)&( A V B)

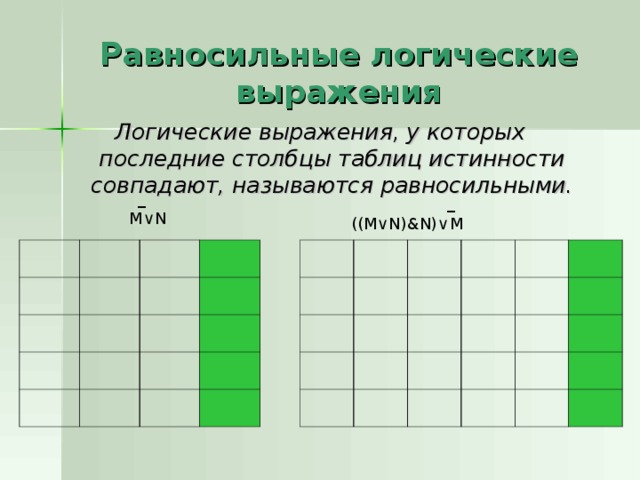
Равносильные логические выражения

Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными.

_

_

M∨N

((M∨N)&N)∨M