Презентация к уроку математики "Формулы сокращенного умножения"

Домашняя работа (самопроверка).

№837

а) (… + 2а) ² = … +12ав +… = …+2·3в·2а+ (2а)²

(3в+2а) ² = (3в) ²+ 2·3в·4а+(2а) ²= 9в²+12ав+4а²

б) (3х + …) ² = …+ … +49у² = (3х) ² + … + (7у)²

(3х+ …) ² =(3х) ² + 2·3х·7у +(7у) ² = 9х²+42ху+ 49у²

№854

ж) (n – 3m) (3m+ n) = n² -(3 m) ² = n² - 9m²

З) (2a – 3b) (3b + 2a) = (2a) ² - (3b) ² = 4a² - 9b²

и) (8с +9d) (9d – 8c) = (9d) ² - (8c) ²= 81d² – 64c²

1) Прочитайте выражение.

a+b, 2(а+b), а-b, 3(а-b), (а+b)²

2(а+b) ², 2аb, 3а²b, (2а)²

а²-b², (а+b) ³, (а-b) ³, 2(а-b)²,

3(а+b)³.

Цель урока:

Закрепление знаний формул квадрата суммы и разности двух выражений, куба суммы и разности двух выражений, разности квадратов и умений в их применении при решении примеров.

Домашняя работа ( самопроверка)

№ 837

а) (… + 2а )² = … +12ав +… = …+2· 3в·2а + (2а)²

(3в+2а)² = (3в)²+ 2·3в·4а+(2а)²= 9в²+12ав+4а²

б) (3х + …)² = …+ … +49у² = (3х)² + … + (7у)²

(3х+ …)² =(3х)² + 2·3х·7у +(7у)² = 9х²+42ху+ 49у²

№ 854

ж ) (n – 3m)(3m+ n) = n² -(3 m)² = n² - 9m²

З ) (2a – 3b)(3b + 2a) = (2a)² - (3b)² = 4a² - 9b²

и) (8с +9 d )(9 d – 8 c ) = (9 d )² - (8 c )²= 81 d ² – 64 c ²

• a+b, 2(а+ b ), а- b , 3(а- b ), (а+ b )²
• 2(а+ b )², 2а b , 3а² b , (2а)²
• а²- b ², (а+ b )³, (а- b ) ³, 2(а- b ) ²,
• 3(а+ b ) ³

• а) сумма квадратов чисел а и b
• б) разность между числом m и удвоенной суммой чисел а и b

• в) квадрат разности чисел b и а

• г) разность квадратов чисел а и b ,

умноженная на сумму этих чисел

составить и прочитать

формулы сокращенного

умножения

(а+ b )²=

(а- b )² =

(а+ b )³=

(а- b )³=

а²- b ² =

II .Представить в виде многочлена

1. (4+х)²=___________________________________

2. (5-х)²=___________________________________

3. (у+3) ²=___________________________________

4. (2 b -3с) ²= ________________________________

5. (а +3)(а- 3)=_______________________________

6. (2х - у)(2х + у)=____________________________

7. (2 – с)³=__________________________________

8. (а + 3)³=__________________________________

• 1. (4+х)²=___________________________________ 2. (5-х)²=___________________________________ 3. (у+3) ²=___________________________________ 4. (2 b -3с) ²= ________________________________ 5. (а +3)(а- 3)=_______________________________ 6. (2х - у)(2х + у)=____________________________ 7. (2 – с)³=__________________________________ 8. (а + 3)³=__________________________________
• 1. (4+х)²=___________________________________ 2. (5-х)²=___________________________________ 3. (у+3) ²=___________________________________ 4. (2 b -3с) ²= ________________________________ 5. (а +3)(а- 3)=_______________________________ 6. (2х - у)(2х + у)=____________________________ 7. (2 – с)³=__________________________________ 8. (а + 3)³=__________________________________
• 1. (4+х)²=___________________________________ 2. (5-х)²=___________________________________ 3. (у+3) ²=___________________________________ 4. (2 b -3с) ²= ________________________________ 5. (а +3)(а- 3)=_______________________________ 6. (2х - у)(2х + у)=____________________________ 7. (2 – с)³=__________________________________ 8. (а + 3)³=__________________________________

9. (а² - с²) ²=_______________________________

• «Щедро одаренный от природы французский философ, писатель, физик, математик Блез Паскаль
• (1623-1662 г.г.), современник Декарта, Ферма он изобрел первую счетную машинку и сделал многое в области математики, которая называется комбинаторикой.»

• Рассмотрим двучлены
• Составим таблицу из коэффициентов
• Заметим закон образования коэффициентов

• ( а+ b )˚=1 1 2º
• (а+ b ) ¹ = а+ b 1 1 2¹
• (а+ b )² = а ² +2а b + b ² 1 2 1 2²
• (а+ b ) ³= а³+3а² b +3а b ²+ b ³ 1 3 3 1 2³

Получение подобных формул можно продолжить. Работая с этими числами, можно строить различные изящные пирамиды.

« Евклид ( 3 век до н.э.) –древнегреческий математик, автор знаменитого трактата «Начала Евклида», посвященного элементарной геометрии, теории чисел. Оказал огромное влияние на развитие математики.»

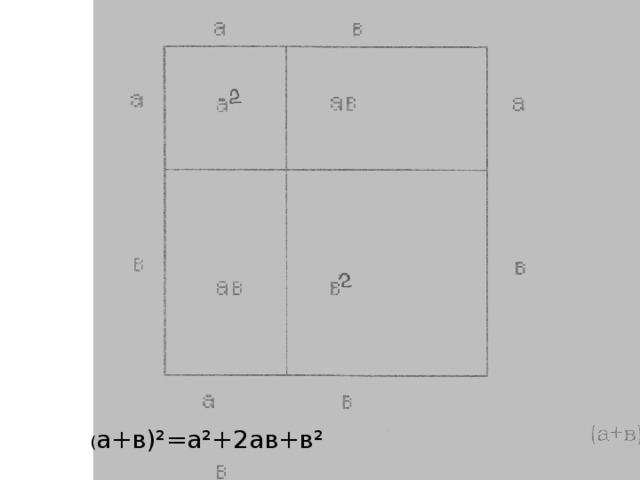
( а+в)²=а²+2ав+в²

(а-в)²=а²-в²-2(а-в)в=а²-в²-2ав+2в²=а²-2ав+в²

(а+в+с)²=а²+в²+с²+2ав+2ас+2вс

• а) (2b+3y)²=
• б) (3а-4b)²=
• в) 4а²+4аb+b²=
• г) а²-4аb+4b²=
• д) 9-b²=
• е) 16х²-25y²=

Ключ к разгадке слова

• (2а+в)²__________________Н
• (а-2b)²___________________И
• 4b²+12by+9y²_____________У
• (3-b)(3+b)________________Ц
• (4х-5 y) (4х+5 y) __ __________А
• 9а²-24аb+16b²____________М

b

V .Дома: П.32-33,

№ 838, 883(а-е)

Продолжить мысль Евклида для (а-в-с)2

VI .Итог урока:

Количество баллов,

полученных за каждое задание занести в таблицу, подвести итог:

№ задания

1

Количество баллов

2

3

4

5

6

итог

Каждый ученик подсчитывает общее количество баллов

и выставляет сам себе оценку по следующим критериям

«5» - 21 – 25 баллов

«4» - 16 – 20 баллов

«3» - 11 – 15 баллов

Игра

Которую можно назвать «Вариации числа»

Придумать комбинации числа 100:

Например

А) 100=50+50

100=38+62 и т.д.

Б) 100= 99+

100= 101-

В) 100=(1+2+3+4) 2

100=1 3 +2 3 +3 3 +4 3

Загадка

Попробуйте изменить

положение одной цифры

и добейтесь, чтобы равенство

102=100 было верным.