
АЛГОРИТМЫ
Составила Миногина Н.П.
Лицей №2 г. Бугульмы

Алгоритмы встречаются нам повсюду, например:
Приготовление торта- алгоритм :
- Замесить тесто
- Раскатать коржи
- Выпечь коржи
- Дать коржам остыть
5. Украсить торт

Пример 1. Решение квадратного уравнения:
1.Найти дискриминант по формуле:
2. Найти первый корень по формуле
x1=(-b+√D)/2a
3. Найти второй корень по формуле
x2=(-b-√D)/2a
4. Записать ответ.

На уроке узнаете:
- Этапы решения задач с помощью компьютера
- Понятие алгоритма
- Свойства алгоритма
- Способы записи алгоритмов
- Основные структуры алгоритма

Этапы решения задач с помощью компьютера
- Постановка задачи
- Построение математической модели
- Разработка алгоритма
- Составление программы на языке программирования
- Отладка и тестирование программы
- Анализ результатов

Алгоритм – это конечная последовательность действий, которая приводит к выполнению поставленной цели или решению задачи.

Исполнитель – это объект, умеющий выполнять определенный набор действий (человек, животное, робот, компьютер). Система команд исполнителя – это все команды, которые исполнитель умеет выполнять. Среда исполнителя – это обстановка, в которой функционирует исполнитель.

Свойства алгоритма
- Дискретность (прерывность, раздельность) – разбиение алгоритма на шаги.
- Понятность – каждый шаг алгоритма должен быть понятен исполнителю.
- Результативность – получение результата за конечное число шагов.
- Массовость – исполнение алгоритма для решения однотипных задач.
- Формальность – возможность выполнять команды механически.

Способы записи алгоритмов
- Словесный (письменно или устно)
- Графический (стрелками, рисунками, блок-схемами)
- Программный

Определение:
Блок-схема – это графическое изображение алгоритма в виде определенным образом связанных между собой нескольких типов блоков.
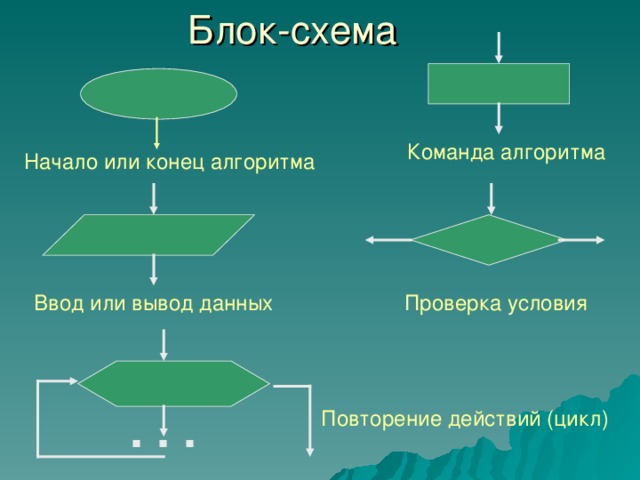
Блок-схема
Команда алгоритма
Начало или конец алгоритма
Проверка условия
Ввод или вывод данных
. . .
Повторение действий (цикл)

Виды алгоритмов:
- Линейный – содержит несколько шагов и все шаги выполняются последовательно друг за другом;
- Разветвляющийся – порядок выполнения шагов изменяется в зависимости от некоторых условий;
- Циклический – определенная последовательность шагов повторяется несколько раз в зависимости от заданной величины (параметра цикла).

1. Линейные (простые)
Команда 1
Команда 2
. . .
Команда N
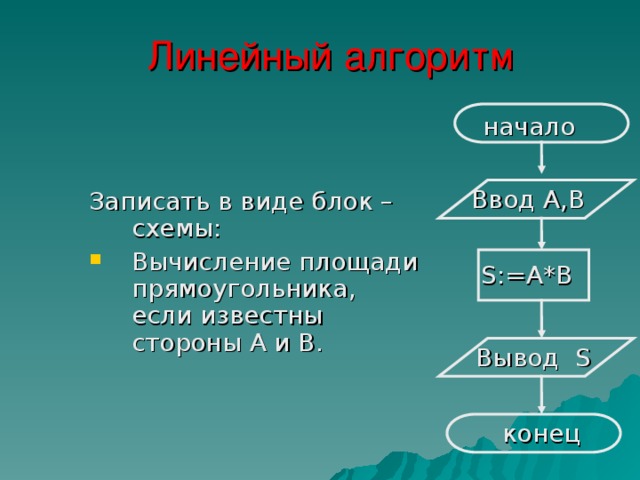
Линейный алгоритм
Записать в виде блок – схемы:
- Вычисл ение площад и прямоугольника, если известны стороны А и В.
начало
Ввод А,В
S:=А*В
Вывод S
конец

Задания
- Построить блок-схему вычисления площади круга радиуса R.
- Построить блок-схему вычисления длины окружности радиуса R.
- Построить блок-схему вычисления площади треугольника со сторонами a,b,c.
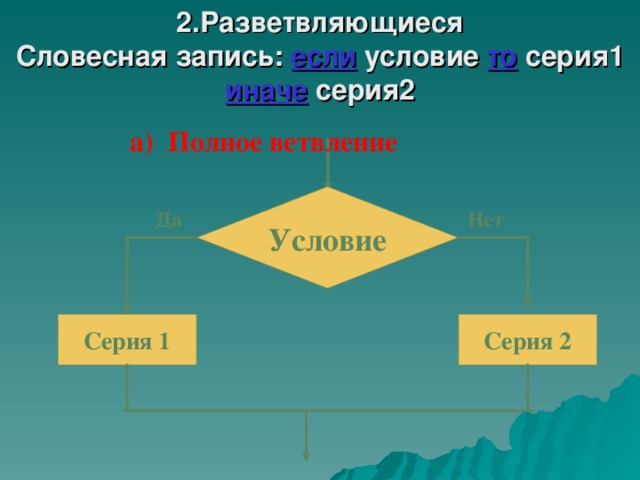
2.Разветвляющиеся Словесная запись: если условие то серия1 иначе серия2
а) Полное ветвление
Условие
Да
Нет
Серия 1
Серия 2
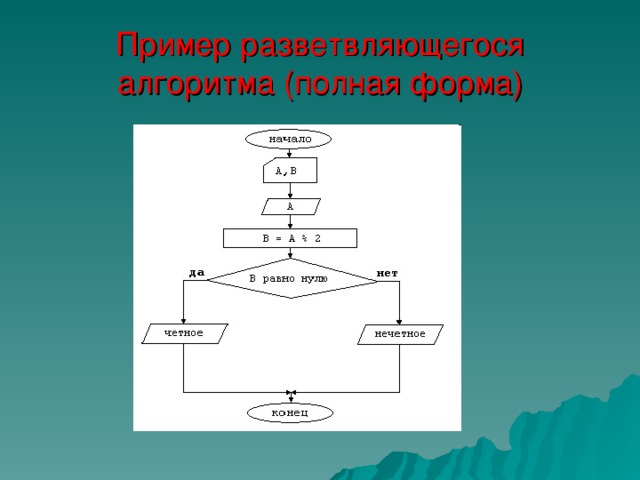
Пример разветвляющегося алгоритма (полная форма)

Задание
- Построить блок-схему определения, имеет ли квадратное уравнение корни (в зависимости от дискриминанта).
- Построить блок-схему нахождения наибольшего из двух чисел a,b.

2. Разветвляющиеся Словесная запись: если условие то серия1
б) Неполное ветвление
Условие
Да
Нет
Серия 1
 0 то у=х-10 вывод у Какое число будет получено в результате выполнения этого алгоритма, если ввести следующие значения х? -12 1 -5 " width="640"
0 то у=х-10 вывод у Какое число будет получено в результате выполнения этого алгоритма, если ввести следующие значения х? -12 1 -5 " width="640"
Имеем алгоритм: ввод х если х то у=2-х если х то у=6 если х 0 то у=х-10 вывод у Какое число будет получено в результате выполнения этого алгоритма, если ввести следующие значения х? -12 1 -5
Задание
- Вывести большее из двух чисел.

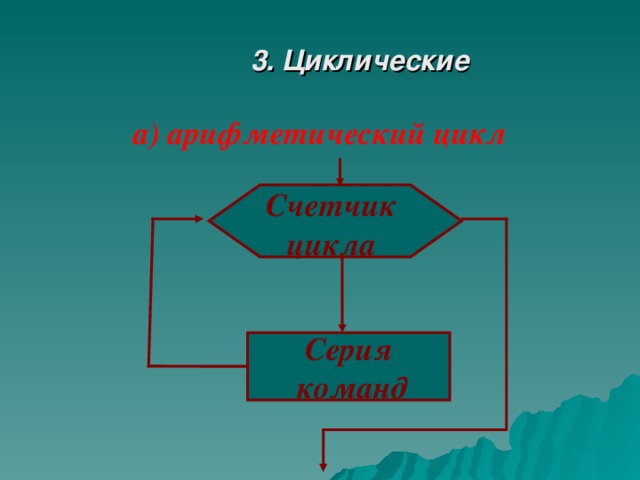
3. Циклические
а) арифметический цикл
Счетчик цикла
Серия
команд
Словесная запись
Для I от А до В
нц
серия
Кц
А – начальное значение, В – конечное значение, I - счетчик

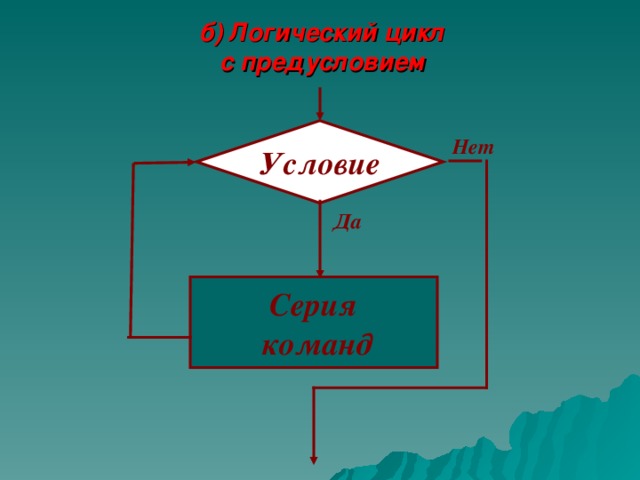
б) Логический цикл с предусловием
Условие
Нет
Да
Серия
команд
Словесная запись
пока условие
нц
Серия
кц

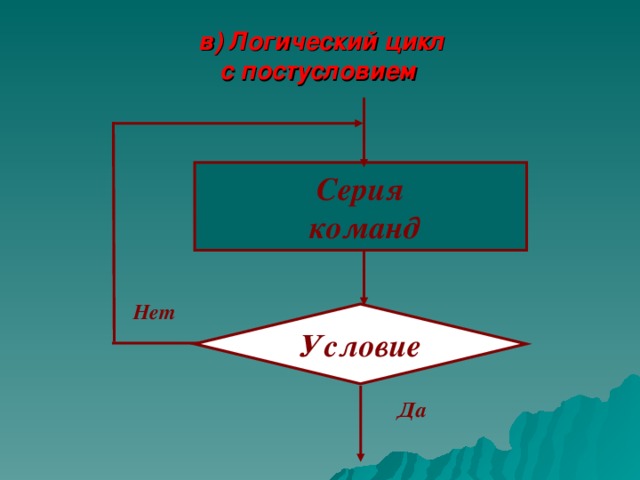
в) Логический цикл с постусловием
Серия
команд
Нет
Условие
Да

Словесная запись
нц
Серия команд
кц
пока условие

Алгоритм – это …
Основные свойства алгоритма …
Алгоритмы можно записать такими способами …
Основные структуры алгоритмов:
1. -
2. -
3. -

1. Выучить конспект
2. Глава 2, § 1, 4.
3. Построить блок-схему нахождения корней квадратного уравнения


 Получите свидетельство
Получите свидетельство Вход
Вход






















 0 то у=х-10 вывод у Какое число будет получено в результате выполнения этого алгоритма, если ввести следующие значения х? -12 1 -5 " width="640"
0 то у=х-10 вывод у Какое число будет получено в результате выполнения этого алгоритма, если ввести следующие значения х? -12 1 -5 " width="640"


















 Презентация к уроку информатики Понятие и виды алгоритмов (0.66 MB)
Презентация к уроку информатики Понятие и виды алгоритмов (0.66 MB)
 1
1 882
882 312
312 Нравится
0
Нравится
0


