Цели:
Изучив данный учебный элемент, Вы узнаете:
о двоичном кодировании информации в компьютере;
о системах счисления;
как представляется числовая информация с помощью систем счисления;
об алгоритме перевода чисел из одной системы счисления в другую.
Оборудование, материалы и вспомогательные средства:
персональный компьютер;
мультимедиапроектор;
презентация урока;
раздаточный материал.
Сопутствующие учебные элементы и пособия:
Учебник Н. Угринович
Электронный учебник «Системы счисления»
Кодирование информации
Кодирование – это операция преобразования знаков или групп знаков одной знаковой системы в знаки или группы знаков другой знаковой системы
Каждая кодировка задаётся своей собственной кодовой таблицей.
Одному и тому же двоичному коду в различных кодировках поставлены в соответствие различные символы.
Двоичное кодирование информации в ПК
В компьютере для представления информации используется двоичное кодирование. Все виды информации в ПК кодируются на машинном языке, в виде логических последовательностей нулей и единиц (бит).
Каждая цифра машинного двоичного кода несёт количество информации, равное одному биту.
Системы счисления
Система счисления – это знаковая система, в которой числа записываются по определённым правилам с помощью символов некоторого алфавита, называемых цифрами.
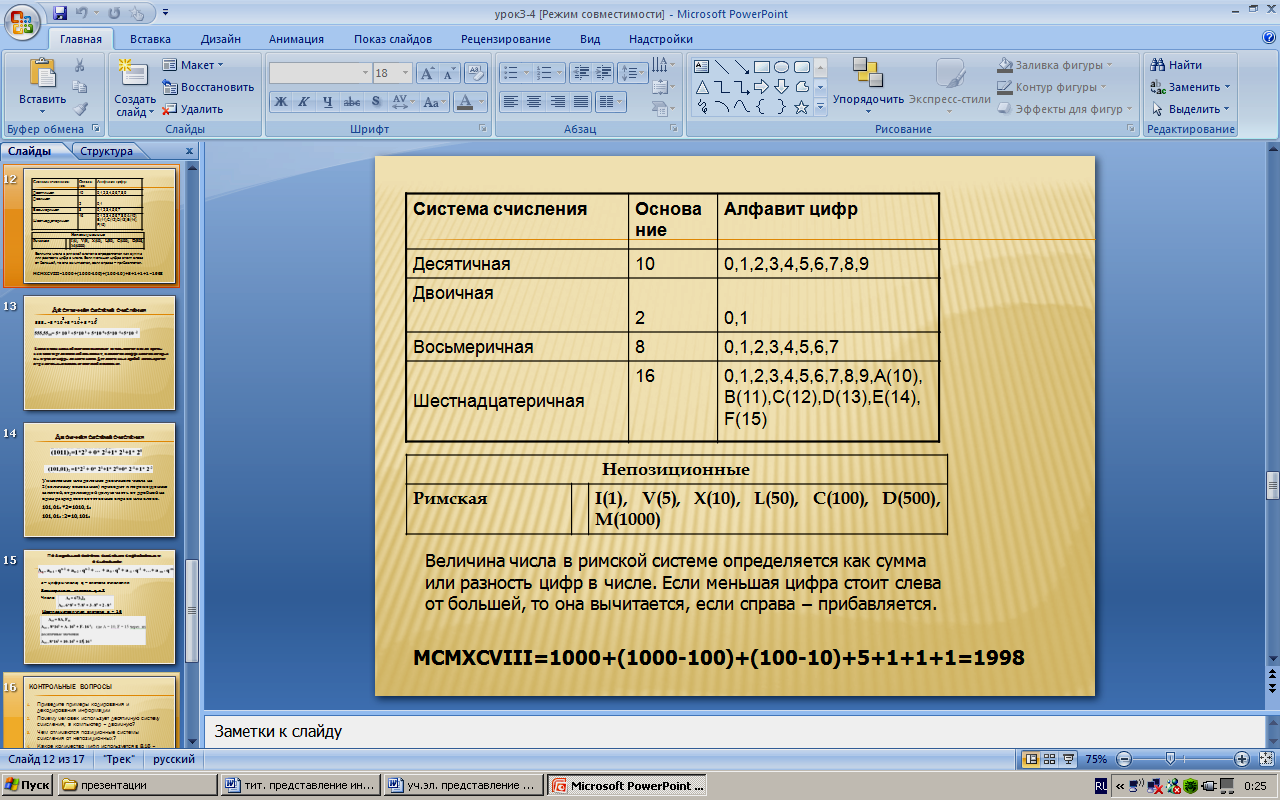
Все системы счисления делятся на две большие группы: позиционные и непозиционные. Позиционные системы характеризуются определенным алфавитом цифр и основанием.
В позиционных системах счисления величина, обозначаемая цифрой, зависит от позиции цифры в числе. 257, 35, 1024.
В непозиционных системах счисления значение цифры не зависит от ее положения в числе.
Величина числа в римской системе определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.
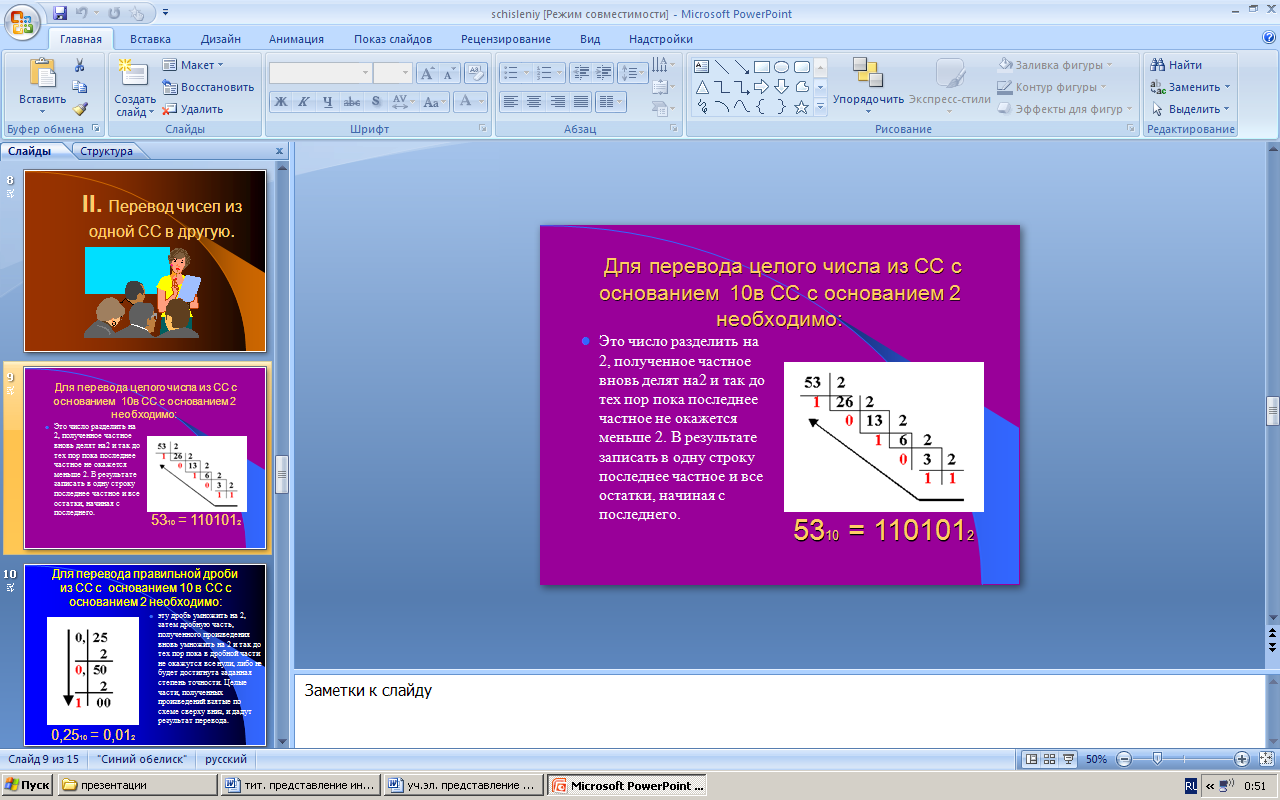
Алгоритм перевода чисел из десятичной системы счисления в двоичную
1.Десятичное число делится нацело на 2, пока это возможно.
2. На каждом шаге записывается остаток от деления.
3. Снизу вверх записываются цифры, начиная с последнего частного и все остатки от деления.
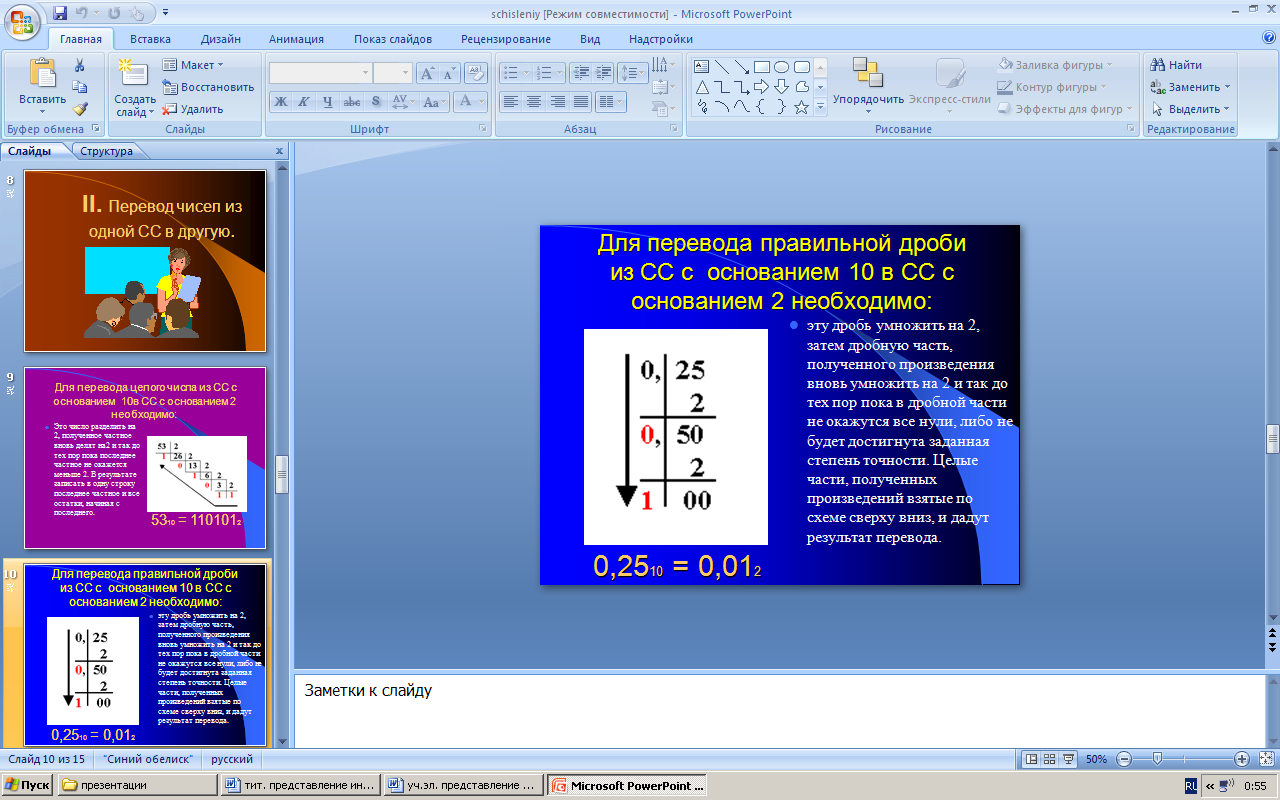
Для перевода правильной дроби из СС с основанием 10 в СС с основанием 2 необходимо: эту дробь умножить на 2, затем дробную часть, полученного произведения вновь умножить на 2 и так до тех пор пока в дробной части не окажутся все нули, либо не будет достигнута заданная степень точности. Целые части, полученных произведений взятые по схеме сверху вниз, и дадут результат перевода.
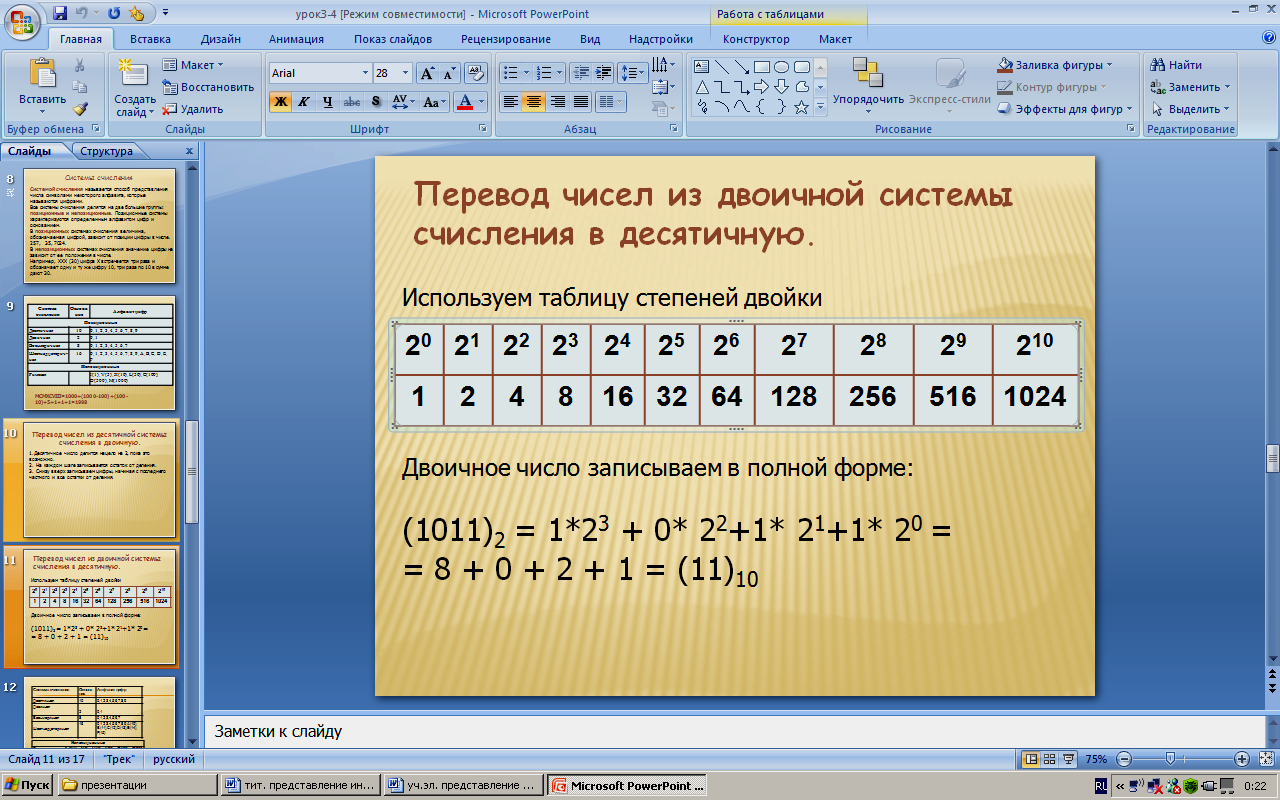
Перевод чисел из двоичной системы счисления в десятичную ССИспользуем таблицу степеней двойки
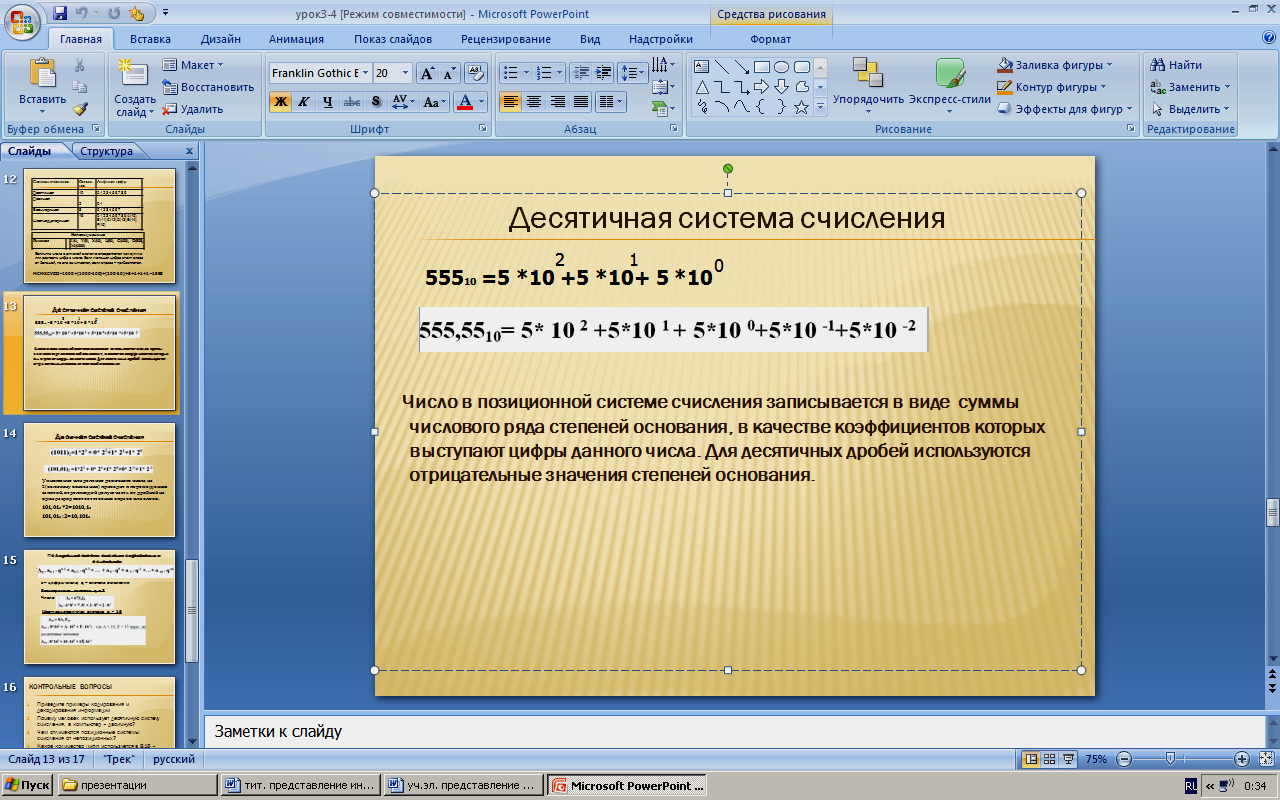
Число в позиционной системе счисления записывается в виде суммы числового ряда степеней основания, в качестве коэффициентов которых выступают цифры данного числа. Для десятичных дробей используются отрицательные значения степеней основания.
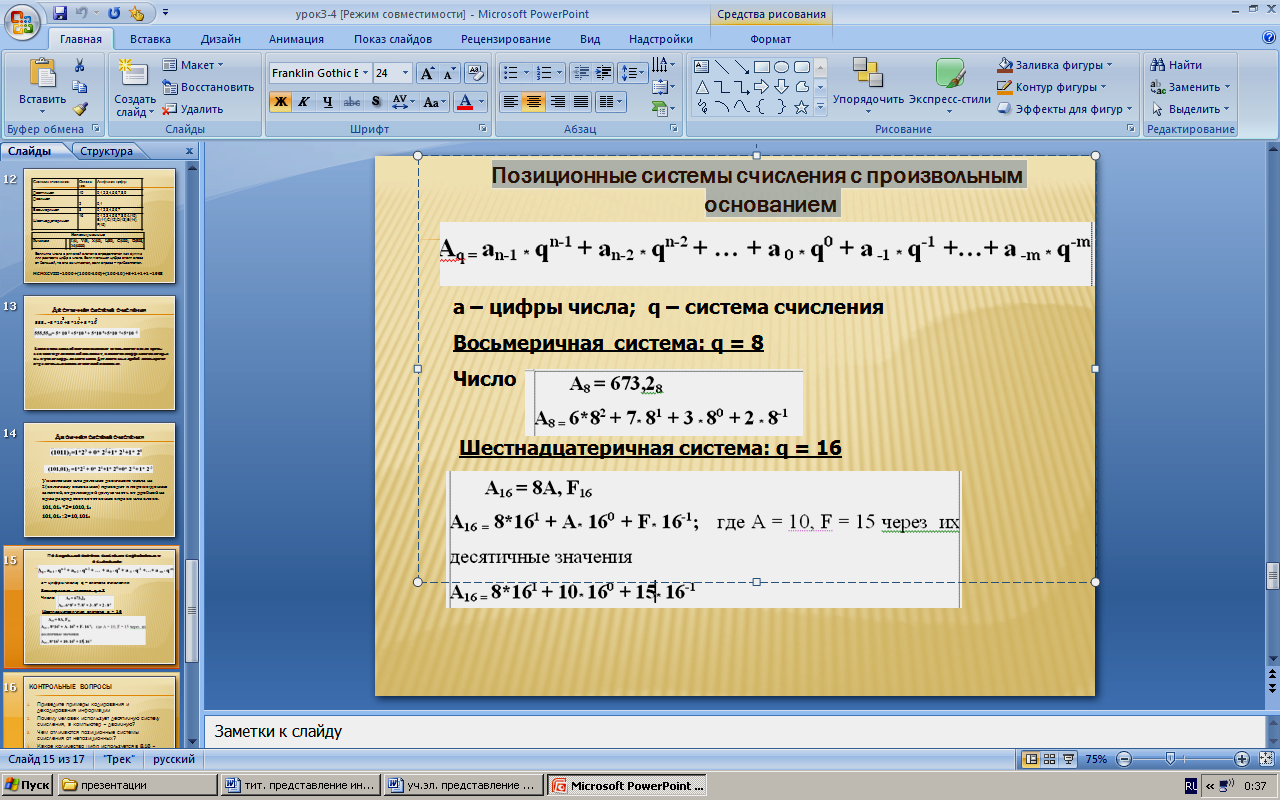
Позиционные системы счисления с произвольным основанием
Перевод чисел из восьмеричной системы счисления в десятичную СС
Перевод чисел из 16-ричной системы счисления в десятичную СС
Перевод чисел из системы с основанием р в систему с основанием q
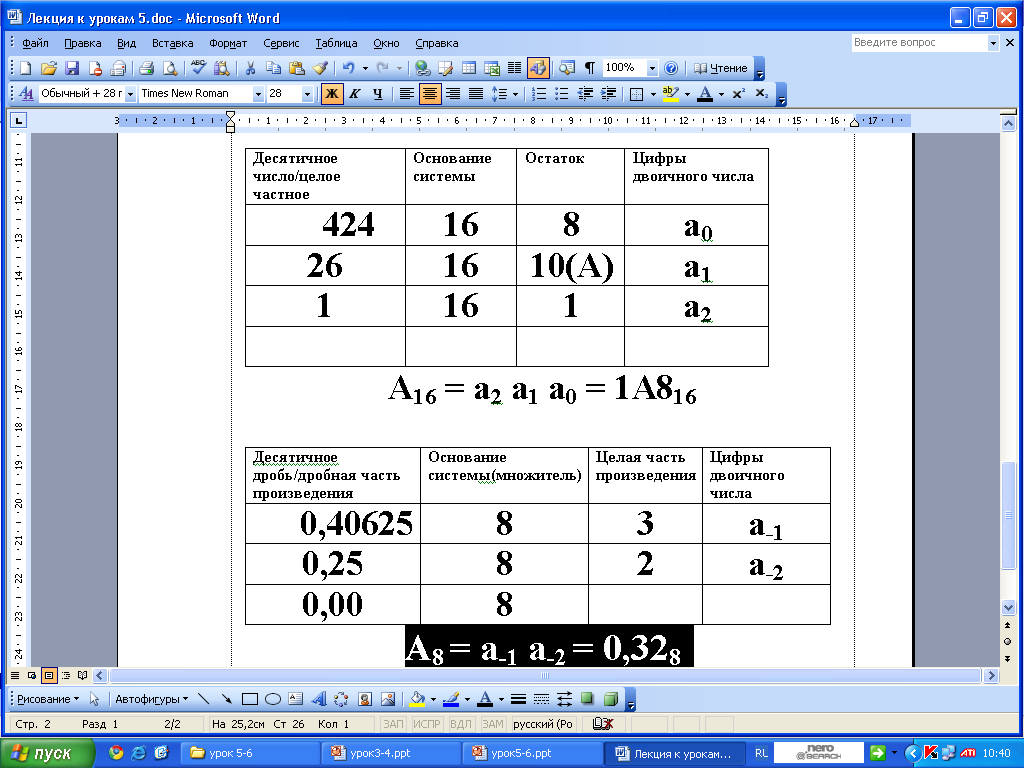
Пример: Перевести 25,2510 в двоичную СС
Сначала - переводим целую часть
Затем - переводим дробную часть
Соединим целую и дробную части и получим ответ
25,2510 = 11001,012
Самостоятельная работа
Записать числа 19,9910 ; 10,102; 64,58; 39,F16 в развёрнутой форме
Какое минимальное основание может иметь система счисления, если в ней записаны числа 23 и 67?
Перевести целые числа 910, 1710, и 24310 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
Перевести числа 3,510 и 47,8510 в двоичную, восьмеричную и шестнадцатеричную системы счисления с точностью до трёх знаков после запятой.
Контрольные вопросы
Каким образом представляется информация в компьютере?
Почему человек использует десятичную систему счисления, а компьютер – двоичную?
Чем отличаются позиционные системы счисления от непозиционных?
Какое количество цифр используется в 8, 16 –ричной системах счисления?
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход





 редмет: «Информатика и ИКТ»
редмет: «Информатика и ИКТ»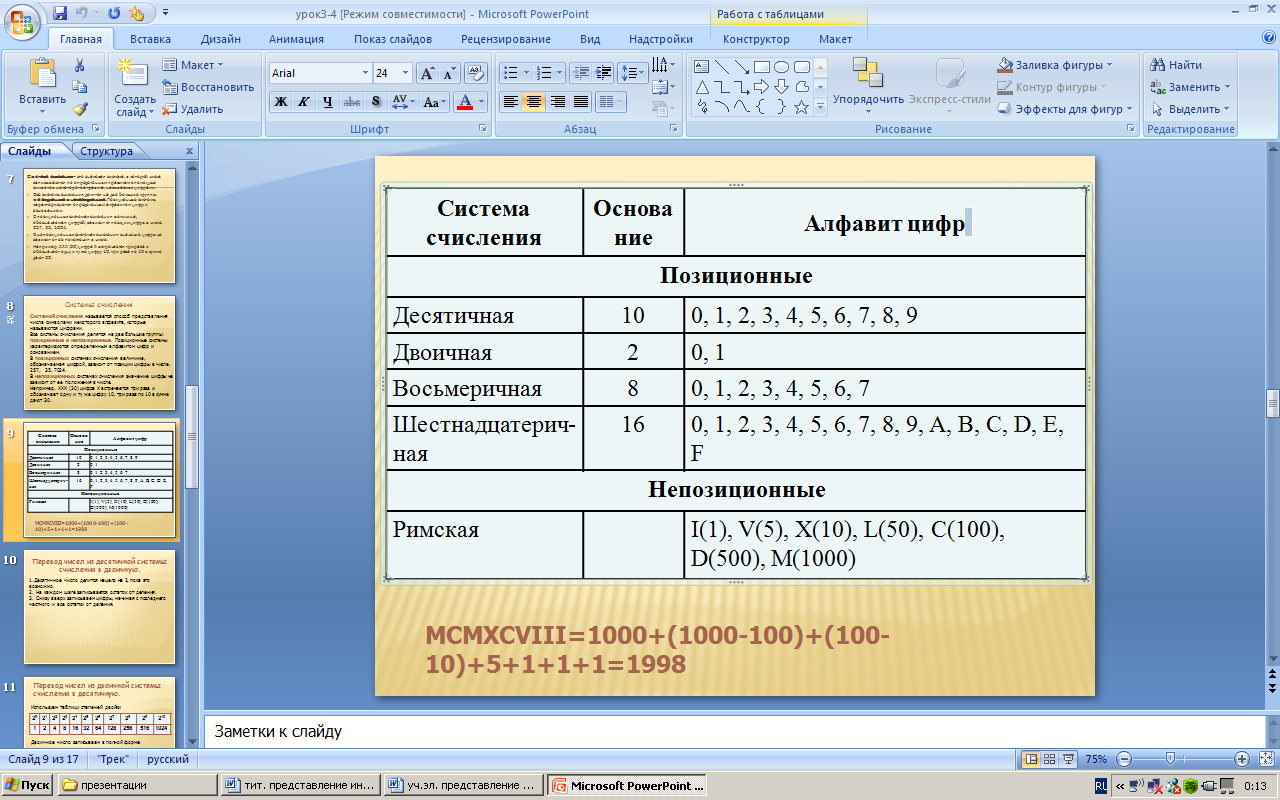
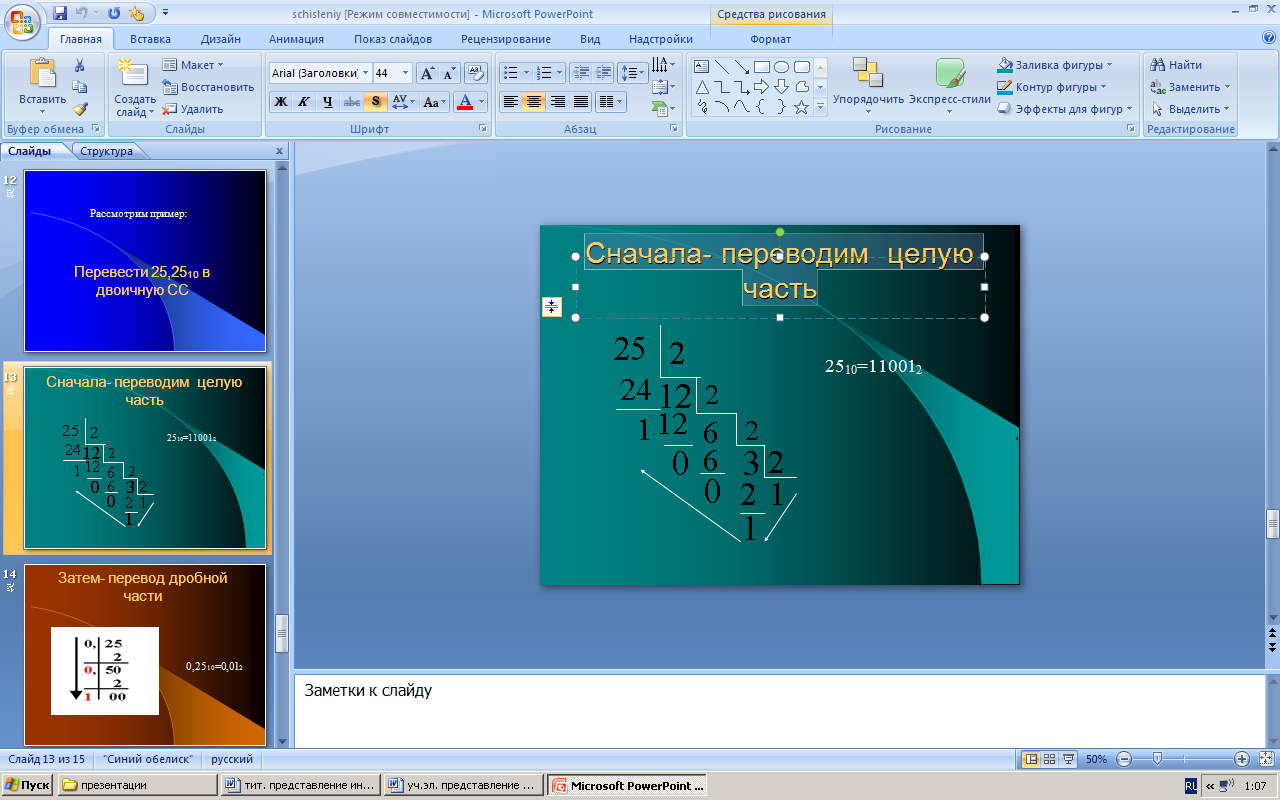 2510=110012
2510=110012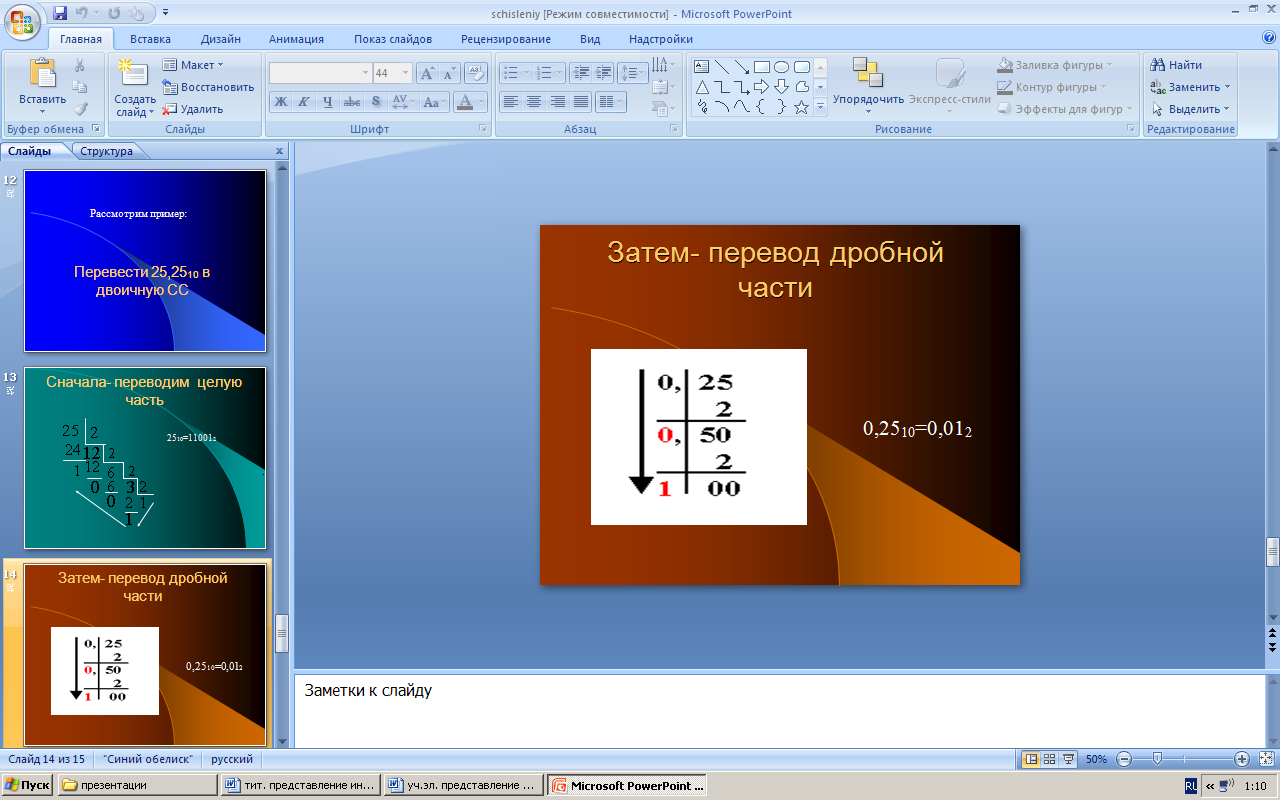 0,2510=0,012
0,2510=0,012 Л-10
Л-10








 Представление информации в двоичной системе счисления (4.28 MB)
Представление информации в двоичной системе счисления (4.28 MB)
 0
0 2319
2319 314
314 Нравится
0
Нравится
0


