Архитектура ЭВМ и вычислительных систем
Методические указания
к выполнению практической работы
Алгебра логики. Логические элементы ПК. Законы логики. Упрощение логических формул
Практическая работа
Цель работы:
Порядок выполнения работы:
Изучение методических рекомендаций
Выполнение практических заданий
Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Что же такое логическое высказывание?
Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:
НЕ Операция, выражаемая словом "не", называется отрицанием и обозначается чертой над высказыванием (или знаком 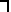 ). Высказывание
). Высказывание 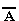 истинно, когда A ложно, и ложно, когда A истинно.
истинно, когда A ложно, и ложно, когда A истинно.
И Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и обозначается точкой " . " (может также обозначаться знаками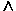 или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны.
или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны.
ИЛИ Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции — дизъюнкция ("или") и в последнюю очередь — импликация.
Связь между алгеброй логики и двоичным кодированием
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Из этого следует два вывода:
одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности
Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ С х е м а И
Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 5.1.
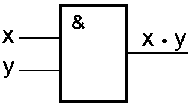
Рис. 5.1
Таблица истинности схемы И
| x | y | x . y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x . y
(читается как "x и y"). Операция конъюнкции на структурных схемах обозначается знаком "&" (читается как "амперсэнд"), являющимся сокращенной записью английского слова and.
С х е м а ИЛИ
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис. 5.2. Знак "1" на схеме — от устаревшего обозначения дизъюнкции как "=1" (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y").
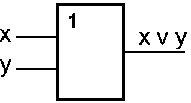
Рис. 5.2
Таблица истинности схемы ИЛИ
| x | y | x v y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
С х е м а НЕ
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z = 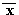 , x где
, x где 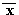 читается как "не x" или "инверсия х".
читается как "не x" или "инверсия х".
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора — на рисунке 5.3
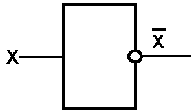
Рис. 5.3
Таблица истинности схемы НЕ
| x | 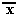 |
| 0 | 1 |
| 1 | 0 |
С х е м а И—НЕ
Схема И—НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом: 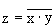 , где
, где 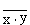 читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представлено на рисунке 5.4.
читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представлено на рисунке 5.4.
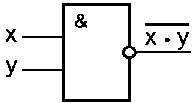
Рис. 5.4
Таблица истинности схемы И—НЕ
| x | y | 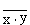 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
С х е м а ИЛИ—НЕ
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом: 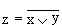 , где
, где 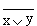 , читается как "инверсия x или y ". Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рис. 5.5.
, читается как "инверсия x или y ". Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рис. 5.5.
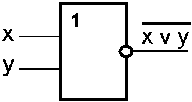
Рис. 5.5
Таблица истинности схемы ИЛИ—НЕ
| x | y | 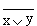 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Основные законы алгебры
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений:
ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ | Закон | Для ИЛИ | Для И |
| Переместительный | 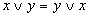 | 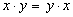 |
| Сочетательный | 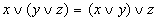 | 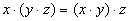 |
| Распределительный | 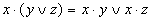 | 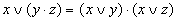 |
| Правила де Моргана | 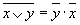 | 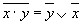 |
| Идемпотенции |  |  |
| Поглощения |  |  |
| Склеивания |  |  |
| Операция переменной с ее инверсией |  |  |
| Операция с константами |  |  |
| Двойного отрицания |  |
Примеры.
1. Составим таблицу истинности для формулы  , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:
, которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:
| Переменные | Промежуточные логические формулы | Формула |
|  |  |  |  |  |  |  |  |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
Из таблицы видно, что при всех наборах значений переменных x и y формула  принимает значение 1, то есть является тождественно истинной.
принимает значение 1, то есть является тождественно истинной.
2. Таблица истинности для формулы  :
:
| Переменные | Промежуточные логические формулы | Формула |
|  |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Из таблицы видно, что при всех наборах значений переменных x и y формула  принимает значение 0, то есть является тождественно ложной.
принимает значение 0, то есть является тождественно ложной.
3. Таблица истинности для формулы  :
:
| Переменные | Промежуточные логические формулы | Формула |
|  |  |  |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Из таблицы видно, что формула  в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.
в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1)
(законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами);
2)
(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией);
3)
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания);
4)
(вводится вспомогательный логический сомножитель ( ); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
5) 
(сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
6)
(выносятся за скобки общие множители; применяется правило операций с константами);
7)
(к отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания);
8) 
(общий множитель x выносится за скобки, комбинируются слагаемые в скобках — первое с третьим и второе с четвертым, к дизъюнкции  применяется правило операции переменной с её инверсией);
применяется правило операции переменной с её инверсией);
9)
(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции);
10) 
(используются правило де Моргана, закон двойного отрицания и закон поглощения).
Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге. Навыки приходят с опытом.
Задания:
1. Упростите следующие формулы, используя законы склеивания:
а) 
б) 
в)
г) 
д) 
Решение:  .
.
2. Упростите следующие формулы, используя законы поглощения:
а) 
б) 
в) 
д) 
е) 
ж) 
з) 
и) 
к) 


 Получите свидетельство
Получите свидетельство Вход
Вход

















 Методические указания к выполнению практической работы по информатике "Алгебра логики. Логические элементы ПК. Законы логики. Упрощение логических формул" (0.19 MB)
Методические указания к выполнению практической работы по информатике "Алгебра логики. Логические элементы ПК. Законы логики. Упрощение логических формул" (0.19 MB)
 0
0 1640
1640 201
201 Нравится
0
Нравится
0



