Практическая работа по теме "Теория пределов. Производная"

Контрольная работа № 2 «Теория пределов. Производная»

Вариант 1

1. Используя определение производной, найти , если

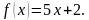
2. Найти производную функции:

.

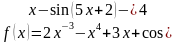1. Написать уравнение касательной к графику функции 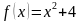в точке с абсциссой .

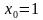2. Найти кинетическую энергию тела через 4с после начала движения, если его масса 25 кг, а закон движения имеет вид .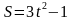

3. Найти точки экстремума и значения функции в этих точках.

Контрольная работа № 2 «Теория пределов. Производная»

Вариант 2

1. Используя определение производной, найти , если

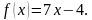
2. Найти производную функции:

.

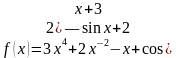1. Написать уравнение касательной к графику функции 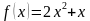в точке с абсциссой .

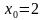2. Скорость тела, движущегося прямолинейно, определяется законом 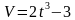(м/с). Какое ускорение будет иметь тело через 3с после начала движения ?

3. Найти точки экстремума и значения функции 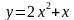в этих точках.

Контрольная работа № 2 «Теория пределов. Производная»

Вариант 3

1. Используя определение производной, найти , если

2. Найти производную функции:

.

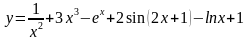1. Написать уравнение касательной к графику функции 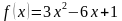в точке с абсциссой .

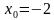2. Материальная точка движется по закону 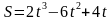(м). найти её ускорение в конце 4с.

3. Найти точки экстремума и значения функции 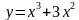в этих точках.

Контрольная работа № 2 «Теория пределов. Производная»

Вариант 4

1. Используя определение производной, найти , если

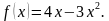
2. Найти производную функции:

.

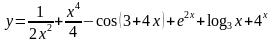1. Написать уравнение касательной к графику функции в точке с абсциссой .

2. Скорость тела, движущегося прямолинейно, определяется законом (м/с). В какой момент времени ускорение будет равно нулю?

3. Найти точки экстремума и значения функции в этих точках.

Контрольная работа № 2 «Теория пределов. Производная»

Вариант 5

1. Используя определение производной, найти , если

2. Найти производную функции:

.

1. Написать уравнение касательной к графику функции в точке с абсциссой .

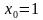2. Два тела движутся прямолинейно: одно по закону , другое - по закону . Определить момент времени, когда скорости этих тел окажутся равными.

3. Найти точки экстремума и значения функции в этих точках.

Контрольная работа № 2 «Теория пределов. Производная»

Вариант 6

1. Используя определение производной, найти , если

2. Найти производную функции:

.

1. Написать уравнение касательной к графику функции в точке с абсциссой .

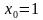2. Точка движется прямолинейно по закону . В какой момент времени её скорость окажется равной нулю?

3. Найти точки экстремума и значения функции в этих точках.