Практическая работа по теме: "Показательные неравенства"

АНО ПОО «Ставропольский гуманитарный колледж»

Практическая работа по теме: «Показательные неравенства»

Подготовила

преподаватель высшей категории

Алибаш И.Л.

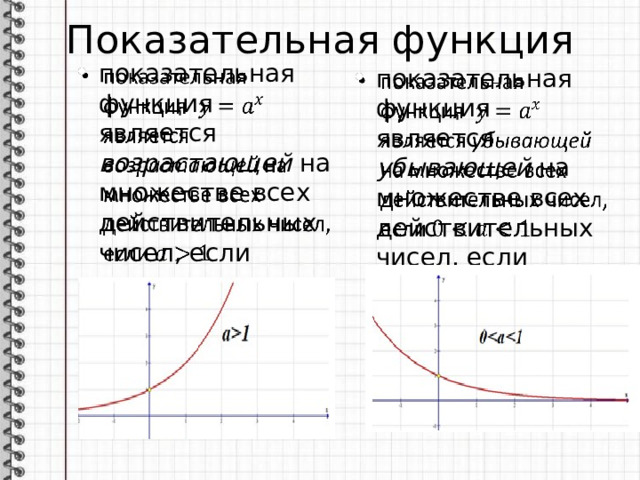
Показательная функция

• показательная функция является возрастающей на множестве всех действительных чисел, если

• показательная функция является убывающей на множестве всех действительных чисел, если

Определите тип функции

Определите тип функции

возрастающая

убывающая

возрастающая

убывающая

Сравните числа

g (x) Показательная функция монотонно возрастает , т.е. большему значению функции соответствует большее значение аргумента и наоборот, следовательно, перейдем к неравенству: f ( x ) x ) или f (x) g (x) Показательная функция монотонно возрастает , т.е. большему значению функции соответствует большее значение аргумента и наоборот, следовательно, перейдем к неравенству: (знак исходного неравенства меняется на противоположный) f ( x ) g ( x ) или f ( x ) x ) (знак исходного неравенства меняется на противоположный) f ( x ) g ( x ) или f ( x ) x ) (знак исходного неравенства не меняется ) (знак исходного неравенства не меняется )   " width="640"

Показательные неравенства

Показательная функция монотонно убывает , т.е. большему значению функции соответствует меньшее значение аргумента и наоборот, следовательно, перейдем к неравенству:

Показательная функция монотонно убывает , т.е. большему значению функции соответствует меньшее значение аргумента и наоборот, следовательно, перейдем к неравенству:

f ( x ) x ) или f (x) g (x)

Показательная функция монотонно возрастает , т.е. большему значению функции соответствует большее значение аргумента и наоборот, следовательно, перейдем к неравенству:

f ( x ) x ) или f (x) g (x)

Показательная функция монотонно возрастает , т.е. большему значению функции соответствует большее значение аргумента и наоборот, следовательно, перейдем к неравенству:

(знак исходного неравенства меняется на противоположный)

f ( x ) g ( x ) или f ( x ) x )

(знак исходного неравенства меняется на противоположный)

f ( x ) g ( x ) или f ( x ) x )

(знак исходного неравенства не меняется )

(знак исходного неравенства не меняется )

0 y=b, b0 1 1 y=b, b=0 y=b, b=0 x x х 0 х 0 0 y=b, b y=b, b 0 " width="640"

Рассмотрим графическое решение показательных неравенств

y

y

y=b, b0

y=b, b0

1

1

y=b, b=0

y=b, b=0

x

x

х 0

х 0

0

y=b, b

y=b, b

0

b (a x ≥ b) выполняются при x R , а неравенства a x b (a x ≤ b) не имеют решения имеют " width="640"

При b ≤ 0 прямая y = b не пересекает график функции y = a x , т.к. расположена ниже кривой y = a x , поэтому неравенства a x b (a x ≥ b) выполняются при x R , а неравенства a x b (a x ≤ b) не имеют решения имеют

Решите неравенство

Ответ:

убывает на всей области определения,

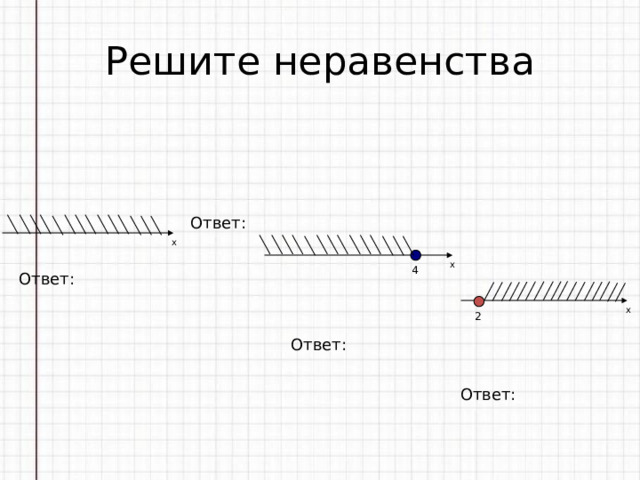
Решите неравенства

Ответ:

x

x

4

Ответ:

x

2

Ответ:

Ответ:

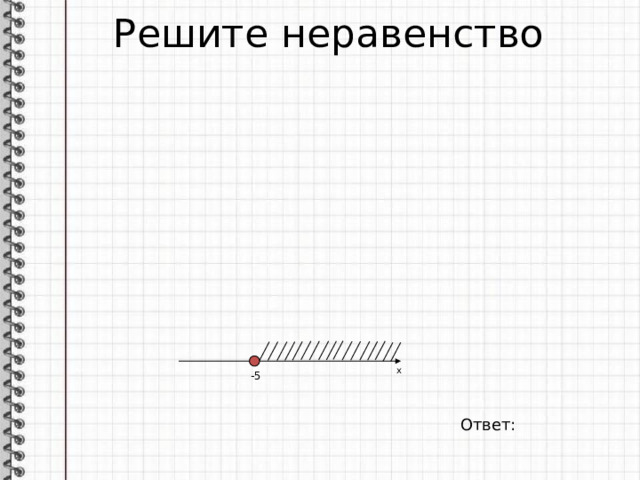
Решите неравенство

x

-5

Ответ:

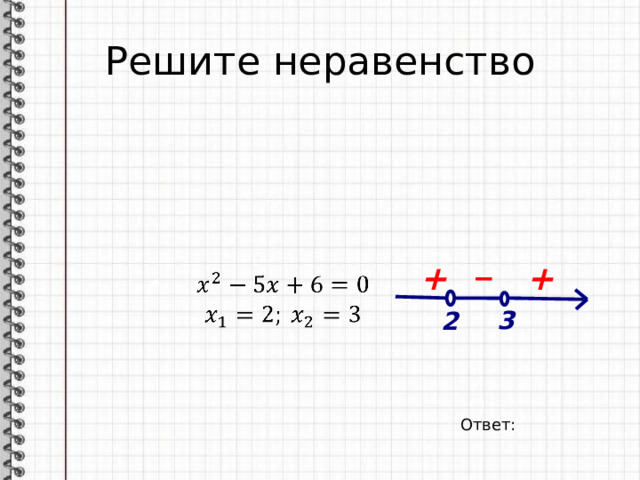
Решите неравенство

_

+

+

•  

3

2

Ответ:

Самостоятельная работа

Вариант 1

Вариант 2

№ 228 (1-3)

№ 228 (4-6)

№ 229 (3-4)

№ 229 (1-2)

Домашнее задание