ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
12 января
2010г
Учитель Козина Н.А.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Повторим определение
Две прямые на плоскости называются параллельными, если они не пересекаются.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Обозначение
a ║ b
a
b
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Стр23. Две прямые перпендикулярные третьей – не пересекаются.
а
B
b
с
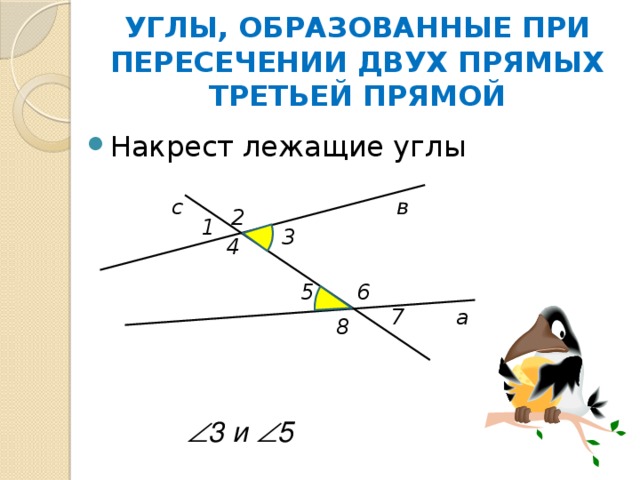
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
5
6
7
а
8
3 и 5
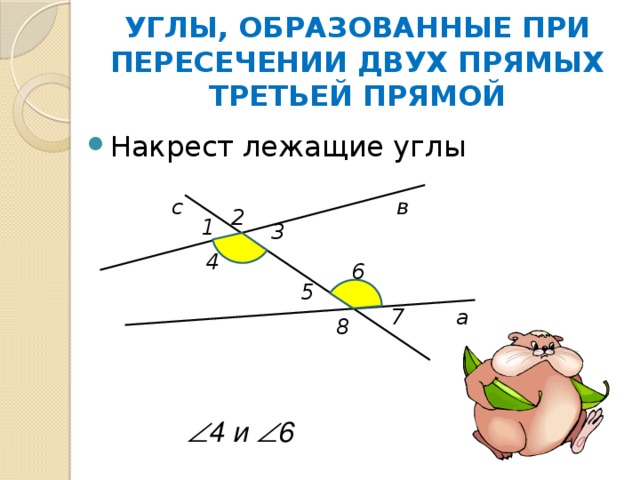
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
4 и 6
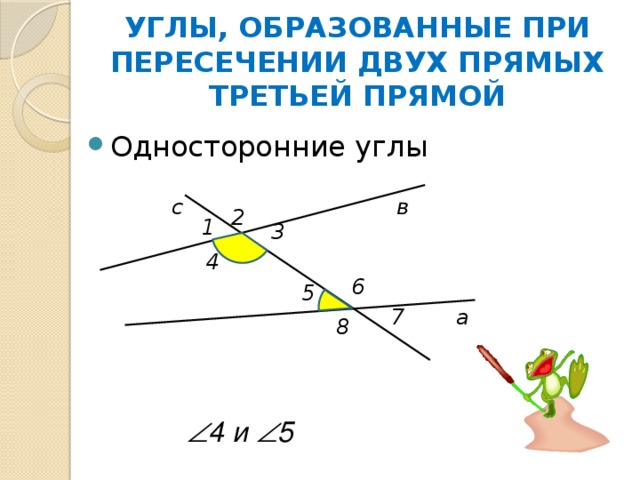
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
4 и 5
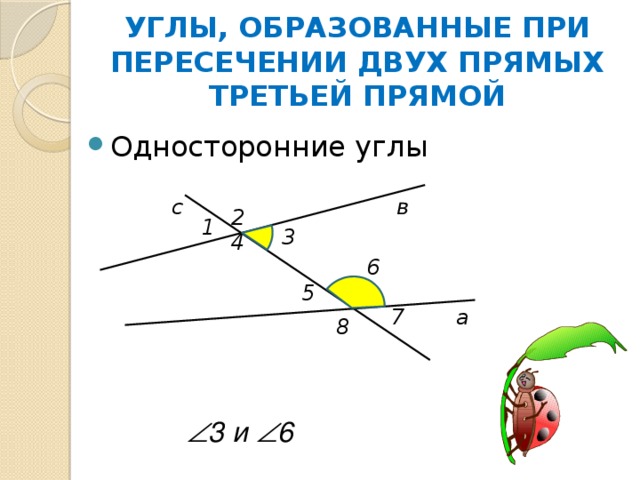
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
3 и 6
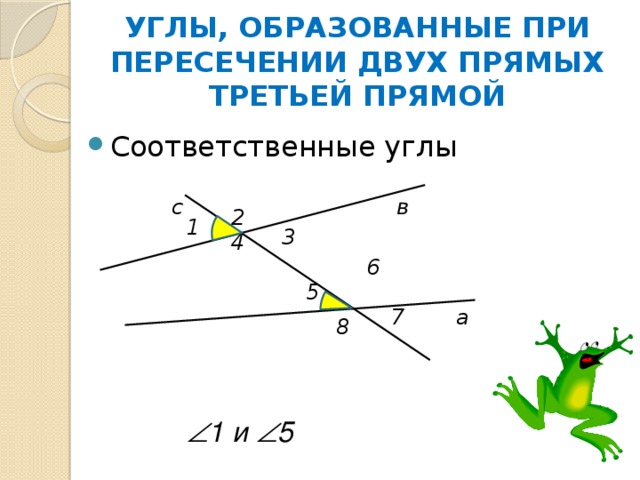
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
1 и 5
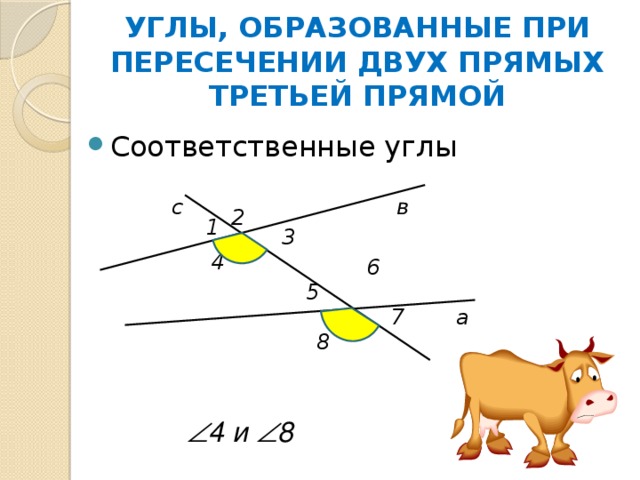
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
4 и 8
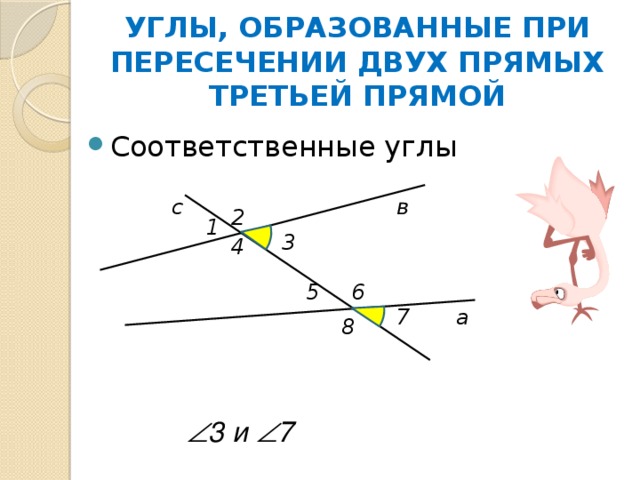
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
5
6
7
а
8
3 и 7
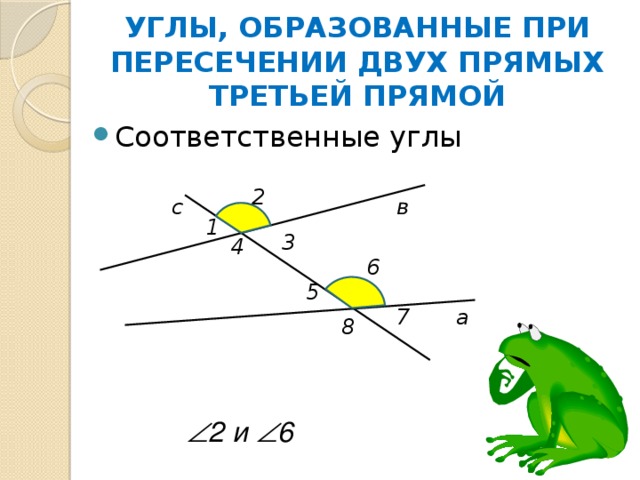
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
2
с
в
1
3
4
6
5
7
а
8
2 и 6
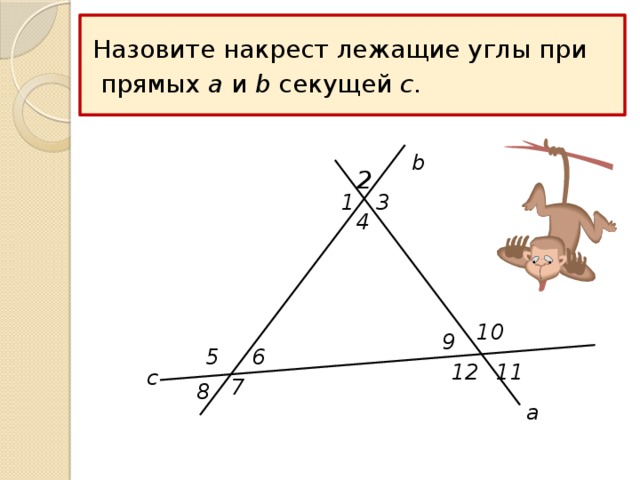
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Назовите накрест лежащие углы при
прямых a и b секущей c .
b
2
1
3
4
10
9
5
6
11
12
с
7
8
а
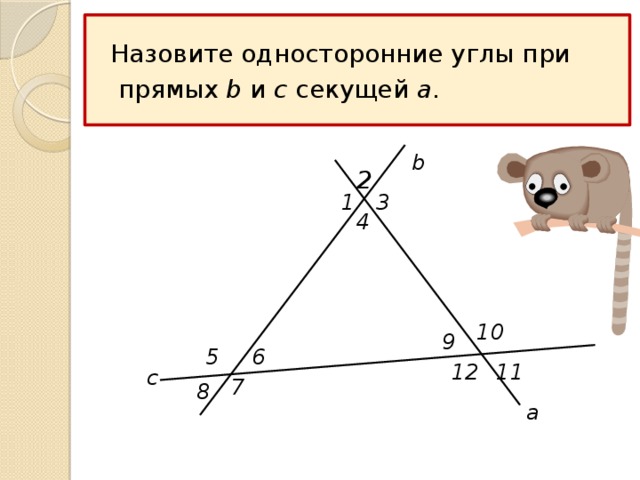
Назовите односторонние углы при
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
прямых b и c секущей a .
b
2
1
3
4
10
9
6
5
11
12
с
7
8
а
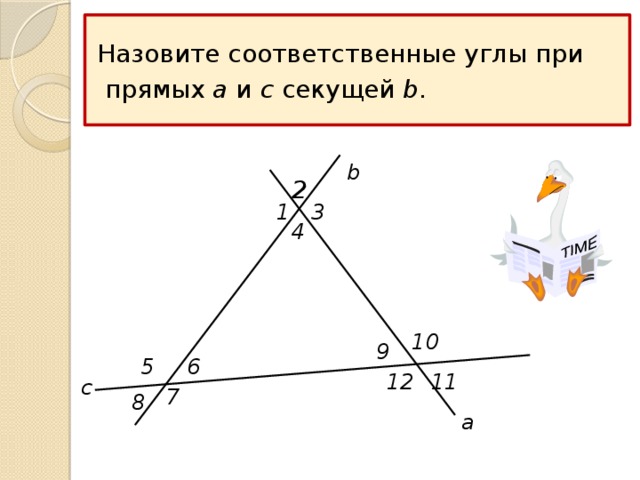
Назовите соответственные углы при
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
прямых a и c секущей b .
b
2
3
1
4
10
9
6
5
11
12
с
7
8
а
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ, ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
ВТОРОЙ ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
ТЕОРЕМА
ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ СООТВЕТСТВЕННЫЕ УГЛЫ РАВНЫ, ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
ТРЕТИЙ ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
ТЕОРЕМА
ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ CУММА ОДНОСТОРОННИХ УГЛОВ РАВНА 180 ⁰ , ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Параллельны ли прямые a и b, если
с
в
d
1
5
2
3
6
4
а
1 = 3
МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Параллельны ли прямые a и b, если
с
в
d
1
5
2
3
6
4
а
1 = 4
МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Параллельны ли прямые a и b, если
с
в
d
1
5
2
3
6
4
а
1 + 2 = 180 ⁰
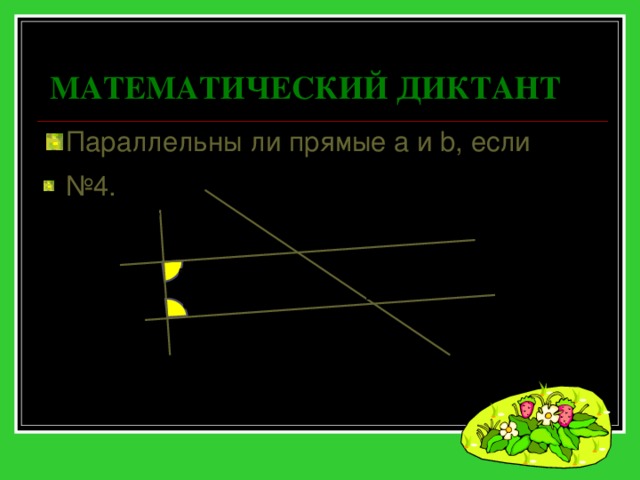
МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Параллельны ли прямые a и b, если
с
в
d
1
5
3
2
6
а
4
5 = 6 = 90 ⁰
МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Параллельны ли прямые a и b, если
с
в
d
1
5
3
2
6
4
а
1 = 2
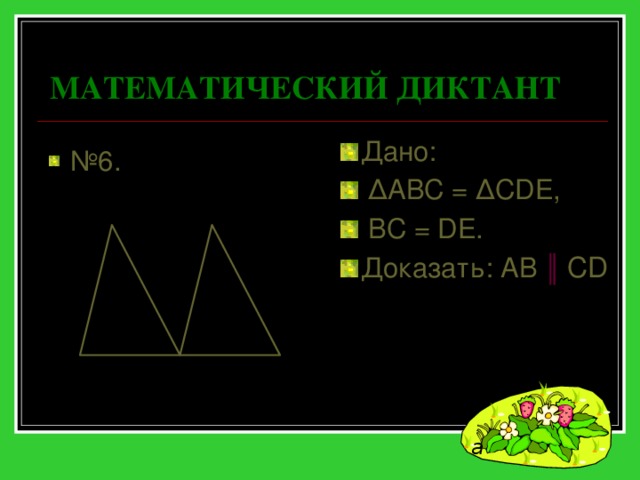
МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Дано:
- ∆ ABC = ∆CDE,
- BC = DE.
- Доказать: AB ║ CD
D
B
A
C
E
а
ОТВЕТЫ
- № 1. Да
- № 2. Да
- № 3. Да.
- № 4. Да
- № 5. Нет
- № 6
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
С помощью угольника и линейки
а
B
b
Построение
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
№ 1. С помощью угольника и линейки проведите 5 параллельных прямых.
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
№ 2. С помощью угольника и линейки через точки A и B проведите прямые, параллельные прямой a.
A
a
B
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
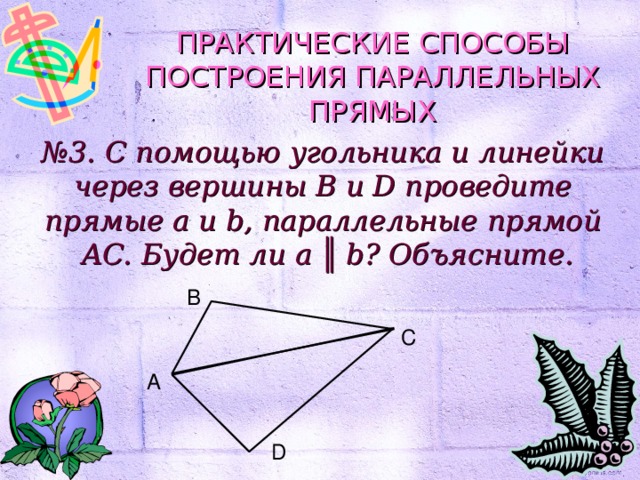
№ 3. С помощью угольника и линейки через вершины B и D проведите прямые a и b, параллельные прямой AC. Будет ли a ║ b? Объясните.
B
C
A
D
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
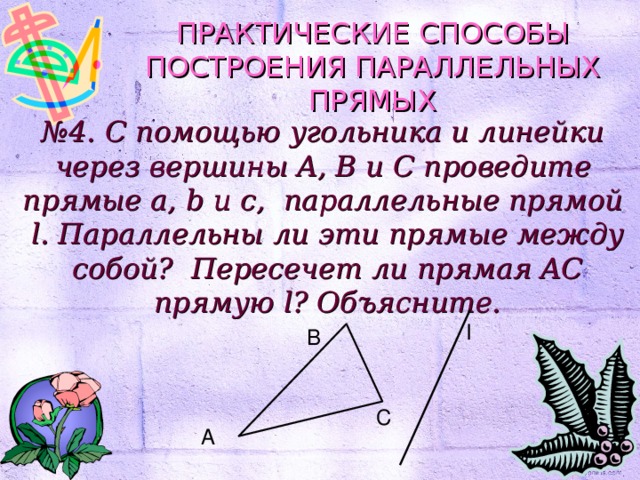
№ 4. С помощью угольника и линейки через вершины A, B и C проведите прямые a, b и c, параллельные прямой l. Параллельны ли эти прямые между собой? Пересечет ли прямая AC прямую l? Объясните.
l
B
C
A
ПРАКТИЧЕСКИЕ СПОСОБЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
№ 5. С помощью циркуля и линейки через вершину С треугольника ABC проведите прямую параллельную AB.
Задание на дом
П. 26 вопрос 6
Решить задачи № 191, 192,194.
Дополнительные задачи.
№ 1. С помощью циркуля и линейки постройте прямую параллельную одной стороне треугольника и проходящую через середину одной из двух других его сторон.
Задание на дом
П. 26 вопрос 6
Решить задачи № 191, 192,194.
Дополнительные задачи.
№ 2. В треугольнике ABС BD – биссектриса ∠ABC, AM = MB.
С помощью циркуля и линейки
постройте прямую, параллельную BD и проходящую через точку М.
РЕШЕНИЕ ЗАДАЧ
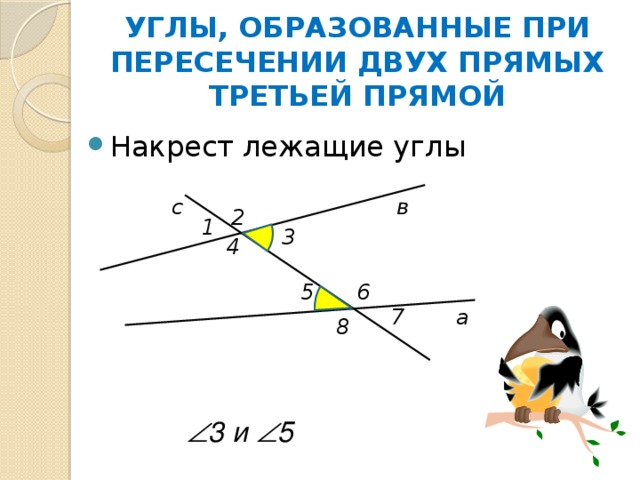
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
5
6
7
а
8
3 и 5
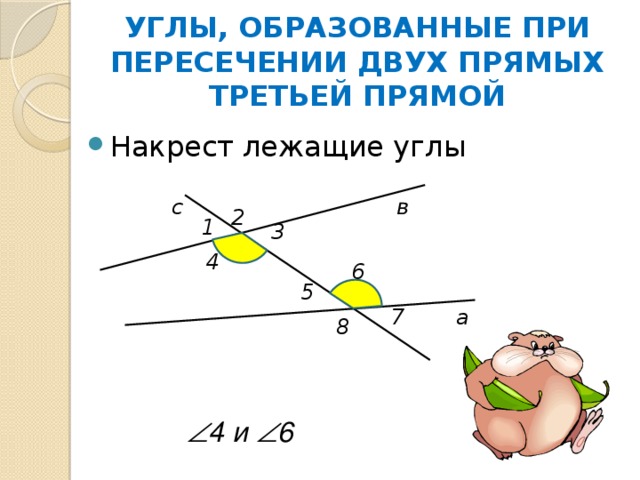
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
4 и 6
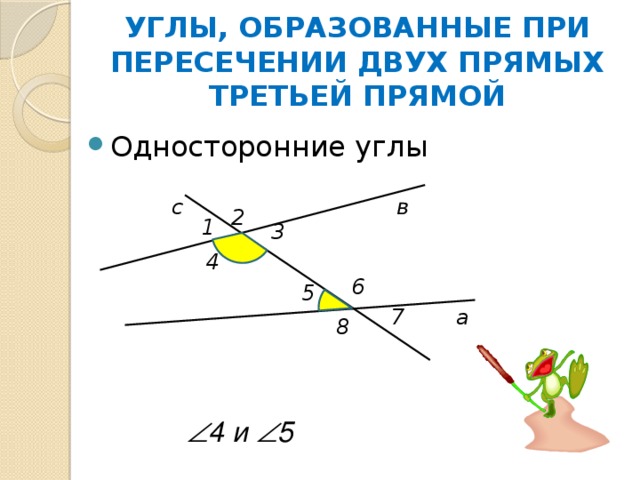
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
4 и 5
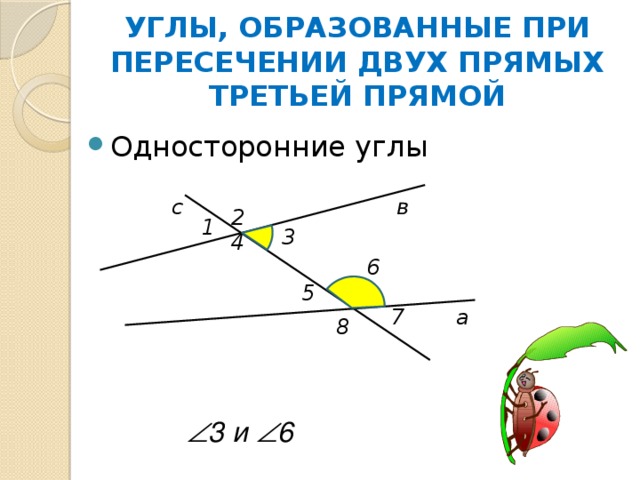
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
3 и 6
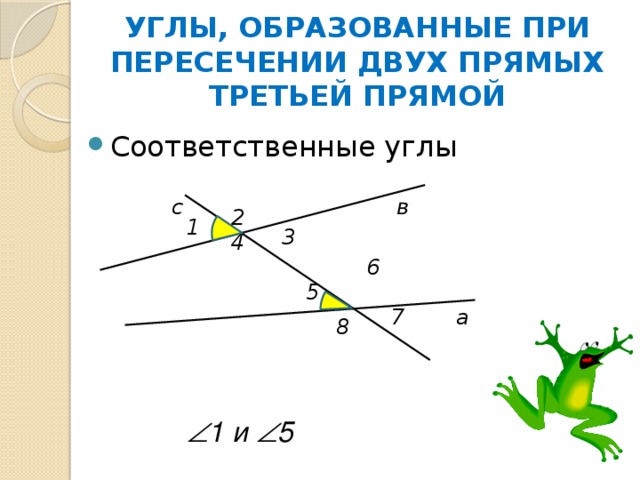
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
1 и 5
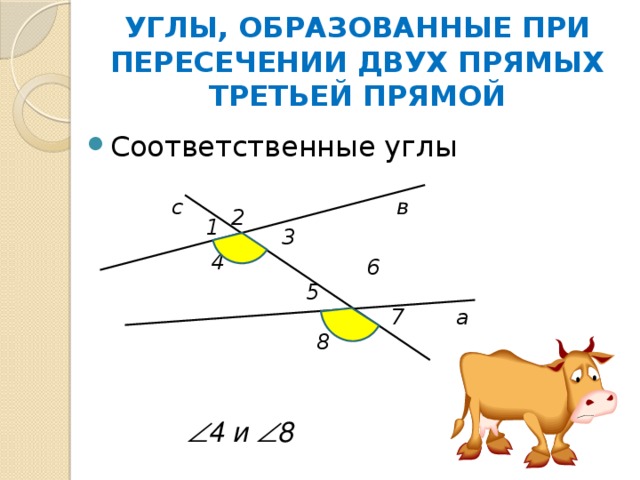
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
4 и 8
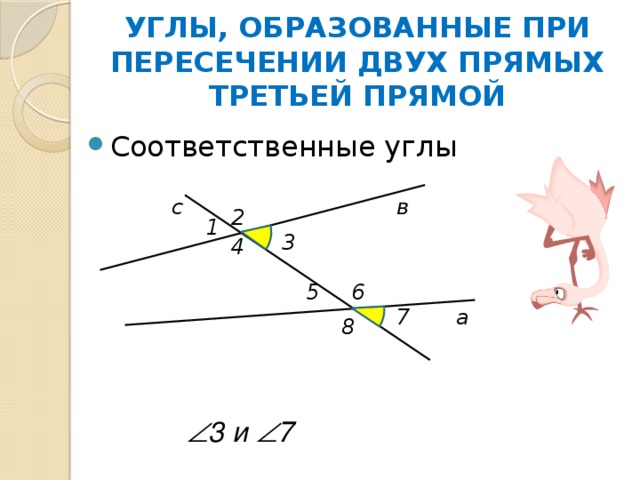
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
5
6
7
а
8
3 и 7
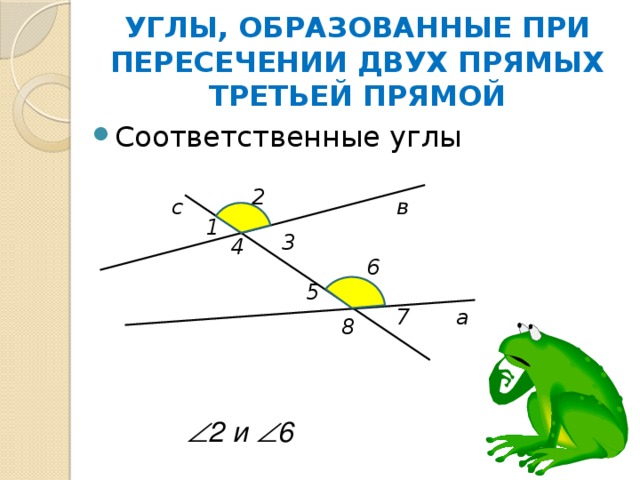
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
2
с
в
1
3
4
6
5
7
а
8
2 и 6
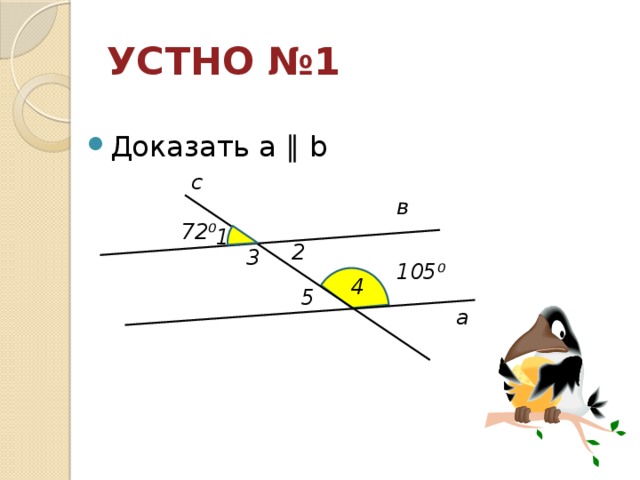
УСТНО №1
с
в
72 ⁰
1
2
3
105 ⁰
4
5
а
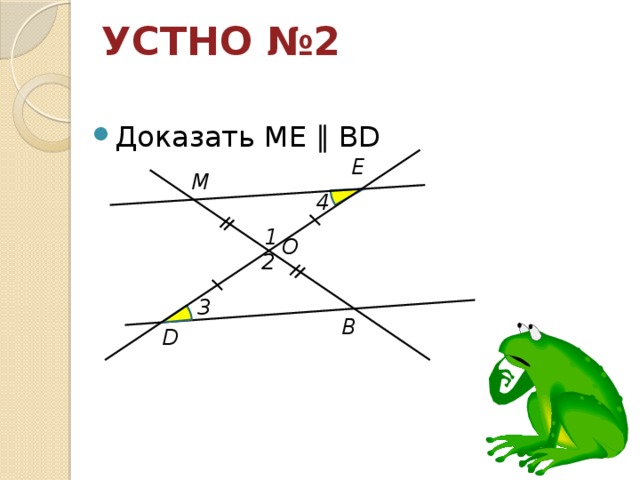
УСТНО №2
E
M
4
1
O
2
3
B
D
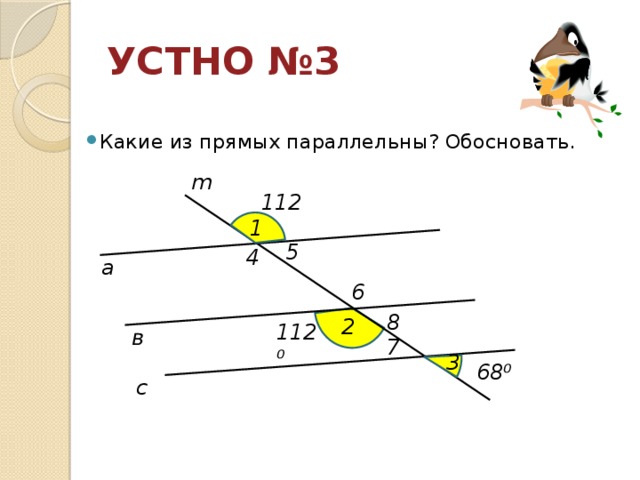
УСТНО №3
- Какие из прямых параллельны? Обосновать.
m
112 ⁰
1
5
4
а
6
8
2
112 ⁰
в
7
3
68 ⁰
с
Получите свидетельство
Вход
Практические способы построения параллельных прямых (0.96 MB)
1
3080
627
Нравится
0
