Разработка математической модели, создание компьютерной модели средствами табличного процессора, построение диаграмм разного типа по результатам проведения эксперимента.

Разработка математической модели, создание компьютерной модели средствами табличного процессора, построение диаграмм разного типа по результатам проведения эксперимента.

Практическая работа
Тема: Моделирование в среде табличного процессора.
Цель: Демонстрация возможностей моделирования в среде табличного процессора MS Excel.
Развитие творческих способностей у учащихся.
Анализ объекта: Компьютерная модель в среде MS Excel.
Задача /12баллов/. Падение с лестницы.
Электрик Петров приставил к стене лестницу длины L, имеющую 10 ступенек, и, поднявшись вверх, остановился на одной из ступенек. В это время концы лестницы начали скользить вдоль стены и пола. Провести исследование, по какой кривой будет падать электрик Петров в зависимости от того, на какой ступеньке он стоит.
Математическая модель:
Обозначим: L – длина лестницы;
N – число ступенек лестницы (по условию задачи N =10);
k – номер ступеньки, на которой стоит электрик и для которой ведется расчет траектории движения.
Для определенности считаем, что ступеньки пронумерованы от 1 до N, начиная снизу. Будем считать, что лестница первоначально занимала вертикальное положение. Это не совсем реально, но удобно для дальнейших расчетов.
При скольжении концов лестницы координата y конца A изменяется от L до 0,
координата x = 0 всегда.
А для конца B наоборот – координата x изменяется от 0 до L, а y = 0.
У промежуточных точек изменяются обе координаты.
В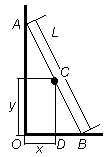 ычислим координаты ступеньки с номером k (см. рисунок). Из рисунка можно заметить, что треугольники OAB и DCB подобны, поэтому их стороны пропорциональны:
ычислим координаты ступеньки с номером k (см. рисунок). Из рисунка можно заметить, что треугольники OAB и DCB подобны, поэтому их стороны пропорциональны:
![]() , при этом
, при этом 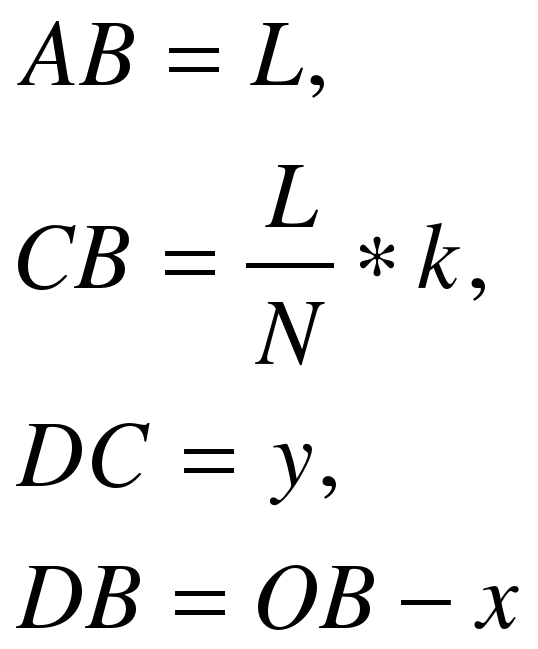
Используя эти выражения, получаем:![]() .
.
Из это пропорции можно получить формулы для координат k-й ступеньки:
![]() (1)
(1)
![]() (2)
(2)
Расстояния OA и OB связаны с теоремой Пифагора: ![]()
Из этой формулы можно выразить OA через OB: ![]() , или наоборот. (3)
, или наоборот. (3)
Траекторию движения ступеньки с электриком будем строить поточечно. Обозначим M – количество точек расчета. В дальнейшем будем вычислять координаты ступеньки для положений лестницы, при которых нижний конец – точка B – перемещается на одну и ту же величину ![]() . Изменяя координату x точки B от 0 до L с шагом
. Изменяя координату x точки B от 0 до L с шагом ![]() , вычисляем длину отрезка OA по формуле (3), а затем координаты ступеньки по формулам (1) и (2).
, вычисляем длину отрезка OA по формуле (3), а затем координаты ступеньки по формулам (1) и (2).
Задание:
Составьте компьютерную модель, проведите расчет координат положения электрика в зависимости от положения лестницы. Пример заполнения электронной таблицы:
| Падение с лестницы | |||
|
|
|
|
|
| Исходные данные |
| ||
| Длина лестницы, м | 1,8 | ||
| Количество ступенек | 10 | ||
| Номер ступеньки, на которой стоит электрик | 8 | ||
| Количество точек расчета | 20 | ||
|
|
|
|
|
| Промежуточные расчеты и результаты | |||
| Шаг изменения положения точки B |
|
| |
|
|
|
|
|
| OB | OA | Координата x | Координата y |
|
|
|
|
|
| Заполнить вниз | Заполнить вниз | Заполнить вниз | Заполнить вниз |
|
|
|
|
|
По результатам вычислений по столбцам C и D постройте диаграмму кривой, по которой движется ступенька с электриком. Убедитесь, что эта кривая похожа на четверть эллипса, сплющенного либо к оси ординат (если номер ступеньки 5), либо к оси абсцисс (если номер ступеньки
Проведите расчет и постройте общую диаграмму кривых для всех ступенек. Для построения общей диаграммы надо скопировать результаты проведения экспериментов в соседние столбцы.
Чему научились:
Создавать модели в среде табличного процессора MS Excel.
Создавать интегрированный документ.
Использовать знания, полученные на предыдущих уроках.
2
 -80%
-80%
 Практическая работа. Моделирование в электронных таблицах (0.12 MB)
Практическая работа. Моделирование в электронных таблицах (0.12 MB)
 1
1 7607
7607 800
800 Нравится
0
Нравится
0
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
 Нравится
0
Нравится
0