Согласовано: ____________зам.дир.по УВР
КСП № 2
| Раздел долгосрочного плана: Повторение курса геометрии 8 класса | Школа: Жалгизкудукская СШ №24 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дата: | ФИО учителя: Лихманова Л.Е. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Класс 9 | Количество присутствующих: | отсутствующих: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема урока | Повторение курса геометрии 8 класса | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 8.1.3.14 вычислять расстояние между двумя точками на плоскости по их координатам;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Цели урока | вычислять расстояние между двумя точками на плоскости по их координатам; определять координаты середины отрезка; записывать уравнение окружности с центром (a,b) и радиусомr; строить окружность по заданному уравнению, в том числе используя программное обеспечение; решать задачи, применяя формулы: расстояния между двумя точками, координат середины отрезка, уравнение окружности с центром (a;b) и радиусом r, уравнение прямой. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Критерии оценивания
| Учащийся достиг цели обучения, если Вычисляют расстояние между двумя точками Определяют координаты середины отрезка Применяют формулу координаты середины отрезка при решении задач Записывают уравнение окружности в стандартном виде по рисунку Записывают уравнение окружности, заданного в общем виде, в стандартной форме | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Языковые цели
| Учащиеся будут: объяснять вывод формул координат середины отрезка и расстояния между точками; комментировать определение координат середины отрезка и расстояния между точками; описывать ход составления уравнений прямой и окружности; аргументировано рассуждать о нахождении координат точек, делящих отрезок в заданном отношении; рассуждать о расположении прямой на координатной плоскости в зависимости от углового коэффициента. Лексика и терминология, специфичная для предмета: прямоугольная система координат на плоскости; уравнение фигуры; координаты середины отрезка; формула расстояния между точками; уравнение окружности; уравнение прямой; центр окружности; угловой коэффициент прямой. Полезные выражения для диалогов и письма: найдём координаты точки А(х;у)– … ; так как точка … –середина отрезка …, то … ; зная координаты точки …, находим координаты …; приравнивая расстояния от … до … , получим; составим уравнение окружности с центром в точке … и радиусом … ; составим уравнение прямой, проходящей через точки … ; точка лежит на прямой, а значит ее координаты удовлетворяют уравнению … . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Привитие ценностей | Уважение, толерантность, сотрудничество, взаимоуважение, патриотизм, честность. Ученики должны будут участвовать в диалоге, особенно с коллегами в парной работе и участвовать в обсуждении класса, развивая коммуникативные навыки. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Межпредметные связи | Информатика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Навыки использования ИКТ | Навыки использования интернет-ресурсов, интерактивной доски, использование графического редактора ГеоГебра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Предварительные знания
| Знание методов решения уравнения, систем уравнений и неравенств; владение навыками построения графиков. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ход урока | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Урок 1 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Начало урока 0-2 мин | 1.Орг.момент. 2. Тема и цели урока, критерии оценивания. |
Слайд №2 -3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Середина урока
2-4 мин
4-6 мин
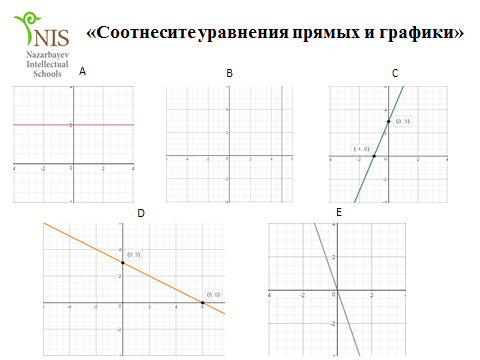
6-11 мин 11-20 мин 20-23 мин 23-30 мин 30-36 мин | К Актуализация знаний 1.
Учащиеся соотносят уравнения и графики прямых, после чего производят проверку в программе GeoGebra. 2. Решить задачу Дескрипторы: - Понимает расположеине графиков в зависимости от знака коэффициента при х. - Верно соотносит функции с их графиками - Знает формулы для построения уравнения прямой по двум точкам. - Использует программное обеспечение для построения графиковGeoGebra Фронтальный опрос Вспомним формулы изученные в рамках этого раздела. Для чего мы их используем? Выход на тему. «Решение задач в координатах». П Задание 1.Исследовательская задача: выведите формулу расстояния между точками. Раздайте учащимся таблицу и координатную плоскость. 1) Построить отрезок АВ на координатной плоскости. 2) Найдите длину отрезка АВ. 3) Как найти длину отрезка, зная координаты концов отрезка? 4) Запишите полученную формулу в таблицу и себе в тетрадь.
Проверка формулы. Задание 2: Заполните таблицу, используя полученную формулу длины отрезка.
Дескрипторы: - выводят формулы длины отрезка -понимают что это и есть формула расстояния между точками. -применяют формулу при решении задачи Г Объедините учащихся в группы. Организуйте работу в группах сменного состава. Для этого создайте несколько групп по 4 учащихся в каждой. Каждому участнику задается свой цвет: красный, зеленый, синий, желтый. Создаются 4 экспертные группы по количеству цветов. Каждая экспертная группа получает индивидуальный материал. Задание для группы «красные». Даны точки К(–2;1), L(5; –6). Найдите: a) координаты точки М , делящей отрезок KL в отношении 2 : 5; Задание для группы «зелёные». Точка P принадлежит отрезку DH. Известно, что отрезок DP в два раза длиннее отрезка HP. Найдите точку H, если D(2; 4), P( Задание для группы «синие». Некоторый отрезок АВ разделен в отношении 2:3:5 (считая от точки А к точке В), его концы – есть точки с координатами А (–11; 1) и В (9; 11). Найдите точки деления данного отрезка. Задание для группы «жёлтые». Точки А (5; –6) и В (–5; 9) – концы отрезка. Найдите координаты точек, которые разделят данный отрезок на пять равных частей. Каждая экспертная группа возвращается в свои группы и объясняет решение своего задания всем учащимся группы. Рефлексия после каждой встречи пар.
Рефлексия этапа Какие задания были интересными? Какие задания вызвали затруднения? В чем была трудность? Над чем предстоит поработать для улучшения результата?
К Устная работа Найдите координаты центра и радиус окружности.
В целях закрепления темы провожу игру «Друзья по часам» Учащиеся ходят по классу и договариваются о встрече в определенное время, после чего когда наступает время встречи они идут к тому человеку с кем договорились и решают задачи. Задание на 12 часов. Дано: А (2; 1), В (0; 3) Найдите: Уравнение прямой АВ Задание на 15 часов. Даны координаты вершин треугольника АВС: А (4; 6), В (–4; 0), С (–1; –4). Какое уравнение является уравнением прямой, содержащей медиану СМ? Задание на 18 часов. Составьте уравнение окружности с центром А (3;2), проходящей через В (7;5) Задание на 21 час. Проверьте, лежат ли точки А (1; –1), В (0; 8), С (–3; –1) на окружности, заданной уравнением (х + 3)2 + (у − 4)2 = 25. Самооценивание по ключам ответов Формативное оценивание Задание 1 Серединами сторон АВ и ВС треугольника АВС являются точки N (3;–1) и M (–4;3) соответственно. Найдите координаты вершин В и С треугольника АВС, если А (5;3) и длину средней линии MN. Задание 2 Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2) Дескрипторы: - использует формулу для нахождения середины отрезка; - применяет формулу для нахождения длины отрезка; - составляет уравнение окружности. |
Слайд №4
https://www.geogebra.org/
Слайд №5
Слайд №6-9
Слайд №10-11
Слайд №12
Слайд №13-17
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Конец урока 36-40 мин | Рефлексия: Что получилось? Что не получилось? Что не учли в работе? Над чем нам надо поработать? Homework (Скрытая дифференциация) Учащиеся выбирают сами 3 задания из таблицы. Обязательное условие, что задания должны быть либо по вертикали (уровень для всех), либо по горизонтали( уровень большинства) или диагонали(уровень для некоторых). |
Приложение 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дифференциация обучения происходит при выполнении индивидуальных заданий
| ФО проводится через наблюдение за работой групп, а также через письменные работы учащихся | Здоровьесберегающие технологии. Используемые физминутки и активные виды деятельности. Пункты, применяемые из Правил техники безопасности на данном уроке. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1:
2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1:
2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Докажите, что четырехугольник АВСД с вершинами в точках: А(-12;6), В (0;11), С (5;-1), Д (-7;-6) - является параллелограммом.
| Найдите координаты середины отрезка ВС, если В(-2;4), С (6;-4).
| Дан треугольник ABC и координаты вершин этого треугольника. Определи длины сторон треугольника и укажи вид этого треугольника.
A(−6;0), B(0;−8) и C(−6;−8).
|
| Даны точки A(8;6) и B(6;2). Найди координаты точек C и D, если известно, что точка B — середина отрезка AC, а точка D — середина отрезка BC.
| Рассчитай расстояние между точками с данными координатами. A(7;2) и B(3;5)
| Даны координаты вектора и конечной точки этого вектора. Определи координаты начальной точки вектора. AB{−7;8} B(−1;8)
|
| Вершины четырехугольника АВСД имеют следующие координаты: А (-3;-1), В (1;2), С(5;-1), Д(1;-4). Докажите, что этот четыреугольник- ромб.
| Найдите периметр треугольника ABC, если его вершины имеют следующие координаты: A(2;2), B(5;7) и C(11;5). | Точка A находится на положительной полуоси Ox, точка B находится на положительной полуоси Oy. Нарисуй прямоугольник AOBC и диагонали прямоугольника. Определи координаты вершин прямоугольника и точки D пересечения диагоналей, если длина стороны OA равна 18, а длина стороны OB равна 6,3.
|

 Получите свидетельство
Получите свидетельство Вход
Вход


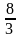 ; 2).
; 2).








 Повторение курса геометрии 8 класса (97.57 KB)
Повторение курса геометрии 8 класса (97.57 KB)
 0
0 378
378 40
40 Нравится
0
Нравится
0




