ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для самостоятельной работы студентов
По дисциплине: МАТЕМАТИКА(включая алгебру и начала математического анализа; геометрию)
Тема: «Функции»
Специальность: 34.02.01 Сестринское дело Курс: 1
(базовой подготовки)
Купино
2020
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным дисциплинам,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.
Купино
2020 г
Пояснительная записка к методическому пособию
Методическое пособие предназначено для повторения теоретических и практических знаний по теме.
Цель пособия – повторить понятия: функции, видов функций, способы задания функции, основные свойства функций,графики функций и подготовится к занятию по теме «Функции».
Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения, свойства и формулы по теме: Функции, тест для самоконтроля и ключи к тесту.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Функции
Определение: Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число y.
Обозначение: y = f(x), где x – независимая переменная (аргумент), y – зависимая переменная (функция). Множество значений x называется областью определения функции (обозначается D(f)). Множество значений y называется областью значений функции (обозначается E(f)). Графиком функции называется множество точек плоскости с координатами (x, f(x))
Способы задания функции.
аналитический способ (с помощью математической формулы);
табличный способ (с помощью таблицы);
описательный способ (с помощью словесного описания);
графический способ (с помощью графика).
Основные свойства функции.
1. Четность и нечетность
Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)
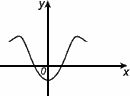
График четной функции симметричен относительно оси 0y
Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)

График нечетной функции симметричен относительно начала координат.
2.Периодичность
Функция f(x) называется периодической с периодом ![]() , если для любого х из области определения f(x) = f(x+Т) = f(x-Т).
, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
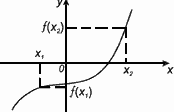
3. Монотонность (возрастание, убывание)
Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 2 выполнено неравенство f(x1)2).

Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 2 выполнено неравенство f(x1) f(x2).

Иными словами:
функция возрастает, если большему значению аргумента соответствует большее значение функции; функция убывает, если большему значению аргумента соответствует меньшее значение функции.
4. Экстремумы
Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х)![]() f(Xmax).
f(Xmax).
Значение Ymax=f(Xmax) называется максимумом этой функции.

Хmax – точка максимума
Уmax – максимум
Точка Хmin называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin , выполнено неравенство f(х)![]() f(Xmin).
f(Xmin).
Значение Ymin=f(Xmin) называется минимумом этой функции.
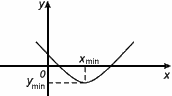
Xmin – точка минимума
Ymin – минимум
Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.
5. Нули функции
Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

Х1,Х2,Х3 – нули функции y = f(x).
Нули функции
Нулём функции y=f(x) называется такое значение аргумента x0, при котором функция обращается в нуль.
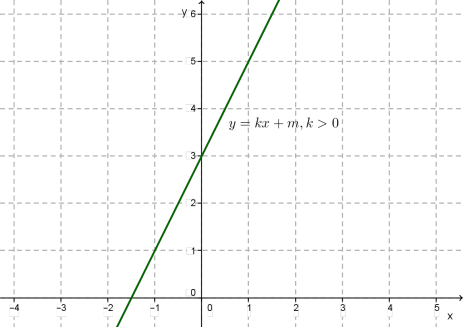
Линейная функция y=kx+m
Графиком функции y=kx+m является прямая.
Свойства функции y=kx+m
1) D(f)=(−∞;+∞);
2) возрастает, если k0, убывает, если k
3) не ограничена ни снизу, ни сверху;
4) нет ни наибольшего, ни наименьшего значений;
5) функция непрерывна
6) E(f)=(−∞;+∞).


Функция y=kx2,k≠0
Графиком функции y=kx2,k≠0 является парабола с вершиной в начале координат и с ветвями, направленными вверх, если k0, и вниз, если k
Свойства функции y=kx2,k≠0
Для случая k0
1) D(f)=(−∞;+∞);
2) убывает на луче (−∞;0], возрастает на луче [0;+∞);
3) ограничена снизу, не ограничена сверху;
4) yнаим=0, наибольшего не существует;
5) функция непрерывна;
6) E(f)=[0;+∞);
7) выпукла вниз.

Свойства функции y=kx2,k≠0
Для случая k
1) D(f)=(−∞;+∞);
2) возрастает на луче (−∞;0], убывает на луче [0;+∞);
3) не ограничена снизу, ограничена сверху;
4) наименьшего значения не существует, yнаиб=0;
5) функция непрерывна;
6) E(f)=(−∞;0];
7) выпукла вверх.

Функция y=k/x
Графиком функции является гипербола.
Свойства функции y=k/x
1) D(f)=(−∞;0)∪(0;+∞);
2) если k0, то функция убывает на открытом луче (−∞;0) и на открытом луче (0;+∞); если k
3) не ограничена ни снизу, ни сверху;
4) нет ни наибольшего, ни наименьшего значений;
5) функция непрерывна на открытом луче (−∞;0) и на открытом луче (0;+∞);
6) E(f)=(−∞;0)∪(0;+∞).


Функция y= √x
Графиком функции y=√x является ветвь параболы.
Свойства функции y=√x
1) D(f)=[0;+∞);
2) возрастает;
3) ограничена снизу, не ограничена сверху;
4)yнаим=0, наибольшего не существует;
5) функция непрерывна;
6) E(f)=[0;+∞);
7) выпукла вверх.

Функция y=|x|
Графиком функции является объединение двух лучей: y=x,x≥0 и y= −x, x≤0.
Свойства функции y=|x|
1) D(f)=(−∞;+∞);
2) убывает на луче (−∞;0], возрастает на луче [0;+∞);
3) ограничена снизу, не ограничена сверху;
4) yнаим=0, наибольшего не существует;
5) функция непрерывна;
6) E(f)=[0;+∞).

Функция y=ax2+bx+c Графиком функции y=ax2+bx+c является парабола с вершиной в точке (x0;y0), где x0=−b/2a,y0=f(x0)=ax02+bx0+c, и с ветвями направленными вверх, если a0, и вниз, если a
Свойства функции y=ax2+bx+c
Для случая a0
1) D(f)=(−∞;+∞);
2) убывает на луче (−∞;−b/2a], возрастает на луче [−b/2a;+∞);
3) ограничена снизу, не ограничена сверху;
4) yнаим=y0, наибольшего не существует;
5) функция непрерывна;
6) E(f)=[y0;+∞);
7) выпукла вниз.

Для случая a
1) D(f)=(−∞;+∞);
2) возрастает на луче (−∞;−b/2a], убывает на луче [−b/2a;+∞);
3) не ограничена снизу, ограничена сверху;
4) наименьшего значения не существует, yнаиб=y0;
5) функция непрерывна;
6) E(f)=(−∞;y0];
7) выпукла вверх.
Тест по теме: Функции


Ключ к тесту по теме Функции
| № | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 3 | 4 | 1 | 2 | 4 |
| 2 | 4 | 1 | 3 | 4 | 3 | 2 |
Критерии оценивания тестовых заданий
6 вопросов 5 (отлично) (5-6 ответов)
6 вопросов 4 (хорошо) (4 ответа)
6 вопросов 3 (удов) (3 ответа)
Литература
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М.: 2018
Башмаков М.И. Сборник задач: учеб. пособие (базовый уровень). 11 кл. – М.: 2012
Интернет-ресурсы
http://school-collection.edu.ru – Электронный учебник «Математика в
школе, XXI век».
http://fcior.edu.ru - информационные, тренировочные и контрольные материалы.
www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов

 Получите свидетельство
Получите свидетельство Вход
Вход











 Пособие по теме Функции (799 KB)
Пособие по теме Функции (799 KB)
 0
0 327
327 6
6 Нравится
0
Нравится
0









