МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
СВЕРДЛОВСКОЙ ОБЛАСТИ
ГБПОУ СО «Исовский геологоразведочный техникум»
«Подготовка к экзаменам студентов второго курса»
Образец решения и оформления решений заданий.
Задание № 1
Исследуйте систему и решите ее методом Крамера.
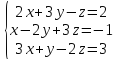 по методу Крамера: составим главный определитель системы
по методу Крамера: составим главный определитель системы
 =
=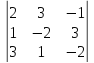 =8+27-1-6-6+6=28, т.к.
=8+27-1-6-6+6=28, т.к.  ≠0, то система имеет единственное решение.
≠0, то система имеет единственное решение.
Находим определители по 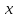 , по
, по 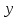 , по
, по 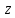 .
.  х =
х =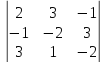 =8+27+1-6-6-6=18
=8+27+1-6-6-6=18
 у =
у =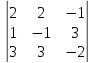 =4+18+-3-3-18+4=2
=4+18+-3-3-18+4=2  z =
z =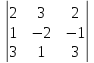 =-12-9+2+12-9+2=18 Находим
=-12-9+2+12-9+2=18 Находим 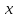 =
=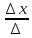 =
=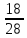 =
=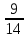 ;
; 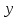 =
=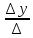 =
=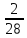 =
=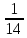 ;
; 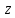 =
=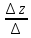 =
=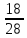 =
=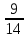 ;
;
Ответ: Система имеет единственное решение. (;
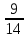 )
)
Задание № 2
Треугольник АВС задан вершинами в системе координат на плоскости.
Найти. 1. Уравнение прямой АВ;
Уравнение высоты, проведённой к стороне АВ;
Уравнение прямой, параллельной к прямой АВ и проходящей через точку С;
Уравнение прямой, перпендикулярной прямой ВС и проходящей через точку А;
Расстояние от точки С до прямой АВ.
Решение: Построим  АВС в системе координат по точкам А(-2;3), В(1;5), С(2;-2)
АВС в системе координат по точкам А(-2;3), В(1;5), С(2;-2)
Найдём координаты всех векторов по формуле:
(хВ - хА; уВ - уА)
(3; 2),
(-3; -2)
(1; -7)
(-1; 7)
(4; -5)
(-4; 5)
1). Уравнение прямой АВ составляем по формуле
Уравнение прямой, проходящей через две точки. Прямая АВ
(А(-2;3), В(1;5))
, ,
, Упростим выражение и приведём его к виду А
х+В
у+С=0 2
(
) = 3
(
), 2х+4 = 3у – 9,
2х - 3у +4 + 9 = 0, 2х - 3у +13 = 0 – Уравнение прямой АВ.
2). Уравнение высоты, проведённой к стороне АВ, это есть прямая СК
(3 ; 2)
По уравнению прямой, проходящей через точку М0() и заданным нормальным вектором
(A;B) A
B
0, где М0(
) = С(2;-2) и
(A;B) =
(3 ; 2). 3
2
0 преобразуем выражение и приведём его к виду А
х+В
у+С=0. 3
х - 6
2
0, получили
3х
2
0 – Уравнение высоты СК, проведённой к стороне АВ.
3). Уравнение прямой, параллельной к прямой АВ и проходящей через точку С;
Прямая МС С(2;-2) и МС
АВ
kМС = kАВ =
=
=
;
kМС =
По уравнению k
, где С(2;-2) = М0(
), k = kМС =
получаем
; преобразуем выражение и приведём его к виду А
х+В
у+С=0.
0 – Уравнение прямой МС
АВ
5). Расстояние от точки С до прямой АВ.
Расстояние от точки С(2;-2) до прямой АВ 2х - 3у +13 = 0 по формуле
d = , где х0 и у0 координаты точки С(2;-2), а А и В – коэффициенты х и у в уравнении АВ 2х - 3у +13 = 0;получим d(С(2;-2; АВ) = =
=
Ответ: 1. 2х - 3у +13 = 0 – Уравнение прямой АВ;
2. 3х
2
0 – Уравнение высоты СК;
3. 0 – Уравнение прямой МС
АВ;
4. ----
5. d(С(2;-2); (АВ))=.
Задание № 3
Дана функция , где
- № варианта.
3.1. Составьте уравнение касательной и нормали к графику данной функции в точке с абсциссой равной
3.
3.2. Тело движется прямолинейно по закону S(t)=y(t), где у(t) – функция
из задания 3.1.
Найдите ускорение движения и путь, пройденный телом, в момент его остановки.
Решаем задачу для В № 41, т.е. а=41
Составим задачу для указанного варианта: ;
= f(x),
3.1.1 Составим уравнение касательной к графику данной функции в точке с абсциссой, равной
3.
Геометрический смысл производной функции – это угловой коэффициент касательной, проведённой к данной кривой 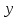 = f(x), в точке М0(
= f(x), в точке М0(), т.е. Kкасательной = у'(х0),
где K – угловой коэффициент касательной.
Уравнение касательной к графику функции в точке М0() имеет вид: у
у0 = у'(х0)
(х
*
Работаем по плану:
Находим у0 = f(
) = f(
) =
=
= )
=
)
(-1
82) =
747 = у0
2). Находим у'(х) = ( =
3
- 82
2
=
164
;
Находим у'(х0) = у'(3) =
164
9 + 492 = 501 = у'(х0)
3). Из 1) и 2) подставим в *, получим у (
747) = 501
(х
у 747 = 501
х
501
х
у
= 0 это есть ур. касательной.
3.1.2 Составим уравнение нормали к графику данной функции в точке с абсциссой, равной
3.
Уравнение нормали к графику функции в точке М0()
у у0 = =
(х
** Нормаль – это прямая, перпендикулярная к касательной в точке касания, значит Kнормали =
4). Из 1) и 2) подставим в **, получим у (
747) =
(х
После преобразований получим: (у+747)501+х+3=0;
х+501у+374250=0 Уравнение нормали
3.2 Тело движется прямолинейно по закону S(t)=y(t), где у(t) – функция
из задания 2.1.
Найдите ускорение движения и путь, пройденный телом, в момент его остановки.
Решаем задачу для В № 41, т.е. а=41
Составим задачу для указанного варианта: ;
Физический смысл первой производной функции = V(t) – скорость в любой момент времени
Физический смысл второй производной функции =
V
(t) = а(t)
ускорение в любой момент времени
Полезно знать, что остановка тела характеризуется
Решение.
1). Найдём первую и вторую производные функции
= (
)
=
164
=
= V
(t) =(
164
)
= 2
164 = а(t)
2). Т.К. тело остановилось, то . Найдём время остановки.
164
= 0
0 (с) или
(с)
Т.К. при = 0 тело начинает движение, то находим
а(164) = 2 = 164(
)
= = (м)
Ответ:
3.1. Уравнение касательной 501х
у
= 0
Уравнение нормали х+501у+374250=0
3.2 а(164) = 164()
(м)
Задание 4
Фигура ограничена линиями: y = x2
x, y = 0
Постройте фигуру в системе координат.
В
Вычислите площадь фигуры.
Вычислите объём тела, полученного вращением фигуры из задания 4.1 вокруг оси ОХ.
АА
Дано: а = 41, y = x2
x = f(х), у = 0
4.1) Вычислим площадь фигуры ОАВ по формуле , где a и b точки пересечения линий = 0
0 или
в этих точка парабола пересекает ось ОХ.
Вычисления: = =
= = = (кв. ед) площадь фигуры
4.2) Вычислим объём тела, полученного вращением фигуры ОАВ вокруг оси ОХ по формуле V=
Вычисления:
V = =
=
=0===
(куб.ед.) – объём тела вращения.
Ответ: Площадь фигуры =
кв. ед. Объём тела вращения V =
куб.ед.
Задание № 5.
Примечание – номер варианта, b=
+1, c=
+2
Найдите общее решение дифференциального уравнения.
(с )
x
y
= 2
a
,
Найдите частное решение дифференциального уравнения.
y =6
(b
)
х + с, если при хo = 0, у = 2, y
;
Составим задачу 5.1). Для 41 варианта: а=41, b=42, c=43
5.1). (43 41)
x
y
= 2
41
2
x
y
= 2
41
, заменим
2x
= 2
41
/
2x
= 2
41
разделяем переменные. Для этого делим обе части уравнения на произведение (х
)
=
=
после сокращения получим:
=
интегрируем обе части, ,
= 41
, зная, что
ln(x
)=lnx + lny, и
, получим
=
=
y =
это есть общее решение диф. ур-ния.
Ответ: общее решение диф. ур-ния y =
5.2). Составим задачу 5.2). Для 41 варианта: а=41, b=42, с=43
y =6
(b
)
х + с, если при хo = 0, у = 2, y
;
y =6
(42
41
)
х + 43
y
=6
х + 43 =
1. **
, /
;
=
3
+ 43
х + C1 =
Найденное значение
подставляем в * и вновь решаем диф. уравнение первого порядка умножаем на
, интегрируем и получаем:
у = +
+
х +
Получили общее решение (ОР) диф. ур.
Для нахождения и
подставляем в систему начальные условия хo = 0, у = 2, y
эти значения подставляем в ОР и получаем частное решение (ЧР)
у = +
+
х +
Ответ: частное решение дифференциального уравнения
при хo = 0, у = 2, y; у =
+
+
х +
Задание № 6
Преобразовать в геометрическую, тригонометрическую и показательную формы комплексное число Z = a
bi, где
– номер варианта, b=
+1.
Примечание: для всех нечётных вариантов – верхние знаки (+ и ), для четных вариантов – нижние (
и +)
Пример 1Составим задание 6) для 41 варианта, т.е. а=41, в=42.
z = 41 42i.
Преобразуем комплексное число в геометрическую, тригонометрическую, показательную формы.
а
1). Изображаем графически это число. Ему соответствует вектор в 4-ой четверти (41;
42).
2).Найдём модуль r =
=
=
. r =
; Из треугольника OaZ находим
tg =
=
=
; →
= arctg
; Т.к.
, то
4). Найденные значения r и вставим в тригонометрическую и показательную формы
z = a bi = r
z = a
bi = r
и получим ответ:z = 41
42i =
Ответ.
Пример 2
Составим задание 6) для 41 варианта, т.е.
а
а=42, в=43. z =
42
43i.
Преобразуем комплексное число в геометрическую, тригонометрическую, показательную формы.
1). Изображаем графически это число. Ему соответствует вектор во 2-ой четверти (41;
42).
2).Найдём модуль r =
=
= = r
; Из треугольника OАМ находим
=
=
=
; →
= arctg
; Т.к.
, то
4). Найденные значения r и вставим в тригонометрическую и показательную формы
z = a bi = r
z = a
bi = r
и получим ответ:
z = 42i+ 43=
Ответ.
КОНЕЦ РАБОТЫ

 Получите свидетельство
Получите свидетельство Вход
Вход











 «Подготовка к экзаменам студентов второго курса» (446.88 KB)
«Подготовка к экзаменам студентов второго курса» (446.88 KB)
 0
0 527
527 3
3 Нравится
0
Нравится
0






