Задачи,которые могли быть теоремами

Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №4» города Балахна

Задачи, которые могли быть теоремами

Выполнила:

Евдокимова Мария

учащаяся 9 класса

МБОУ СОШ №4

г. Балахна

Руководитель:

Хмылова Ольга Валерьевна

учитель математики

г.Балахна

2017 г.

На уроках геометрии мы решаем много задач, среди которых встречаются задачи, которые можно использовать в качестве теорем

• Гипотеза: предполагается, что некоторые задачи, могут оказаться теоремами.
• Цель моей работы: найти такие задачи для прямоугольного треугольника, которые могли бы быть теоремами, сформулировать их в виде утверждений, затем доказать эти утверждения.

• Объект исследования: прямоугольный треугольник и его элементы (медиана, биссектриса, высота).
• Предмет исследования: задачи и их доказательства.

Теоре́ма — утверждение, выводимое в рамках рассматриваемой теории из множества аксиом посредством использования конечного множества правил вывода.

Всякий шаг доказательства состоит из трех частей:

  1) предложение (аксиома, теорема, определение), на основе которого производится этот шаг доказательства; это основание шага доказательства называется посылкой или аргументом;

2) логическое рассуждение, в процессе которого посылка применяется к условиям теоремы или к ранее полученным следствиям;

3) логическое следствие применения посылки к условиям или ранее полученным следствиям.

1. В прямоугольном треугольнике, с острым углом в 30° высота и медиана, проведенные из вершины прямого угла, делят прямой угол на три равные части

Задача: В прямоугольном треугольнике АВС с острым углом в 30 0 , найти угол между высотой и медианой проведенных из вершины прямого угла к гипотенузе.

Справедливо и обратное утверждение:

2. Если в прямоугольном треугольнике высота и медиана проведенные к гипотенузе делят прямой угол на три равные части, то у этого треугольника острые углы 30° и 60°

3. В прямоугольном треугольнике угол между медианой и высотой прямого угла равен разности острых углов

Задача: Острые углы прямоугольного треугольника равны 24 о  и 66 о . Найдите угол между высотой и медианой, проведенными из вершины прямого угла.

4 . Если медиана, проведенная к гипотенузе прямоугольного треугольника делит прямой угол в отношении 1 : 2, то острые углы делятся в этом же отношении

Задача: В прямоугольнике угол между большей стороной и одной из диагонали 30 0 . Найти угол между меньшей стороной и другой диагональю.

Справедливо и обратное утверждение: 5. В прямоугольном треугольнике с острым углом в 30° медиана, проведенная из вершины прямого угла, делит его в отношении 1:2

6. Биссектриса прямого угла в прямоугольном треугольнике с неравными катетами делит пополам угол между медианой и высотой, проведенными к гипотенузе

Задача: Дан прямоугольный треугольник с неравными катетами. Найдите угол между биссектрисой и медианой, если угол между медианой и высотой проведенных к гипотенузе 30 0 .

7. В прямоугольном треугольнике угол между медианой и биссектрисой прямого угла равен полуразности острых углов прямоугольного треугольника

Задача: Найдите угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, если  А = 31 о ,  В = 59 о .

8. В прямоугольном треугольнике угол между высотой и биссектрисой прямого угла равен полуразности острых углов прямоугольного треугольника

Задача: Острые углы прямоугольного треугольника равны 25 о и 65 о . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. 

9. Угол между высотой и биссектрисой, выходящих из одной вершины, равен полуразности других углов треугольника

Задача: В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.

Элементы треугольника

Высота и медиана

Прямая теорема

Медиана

Обратная теорема

1.В прямоугольном треугольнике, с острым углом в 30° высота и медиана, проведенные из вершины прямого угла, делят прямой угол на три равные части.

2.Угол между медианой и высотой прямого угла прямоугольного треугольника равен разности острых углов.

Если медиана, проведенная к гипотенузе прямоугольного треугольника делит прямой угол в отношении 1:2, то у острые углы делятся в этом же отношении.

Биссектриса, медиана, высота

Если в прямоугольном треугольнике высота и медиана проведенные к гипотенузе делят прямой угол на три равные части, то у этого треугольника острые углы 30° и 60°.

В прямоугольном треугольнике с острым углом в 30° медиана, проведенная из вершины прямого угла, делит его в отношении 1:2.

Биссектриса прямого угла в любом прямоугольном треугольнике с неравными катетами делит пополам угол между медианой и высотой, проведенными к гипотенузе.

Медиана и биссектриса

В прямоугольном треугольнике угол между медианой и биссектрисой прямого угла равен полуразности острых углов.

Высота и биссектриса

1.В прямоугольном треугольнике угол между высотой и биссектрисой прямого угла равен полуразности острых углов.

2.В треугольнике угол между высотой и биссектрисой, выходящие из одной вершины равен полуразности острых углов.

Задача: В прямоугольнике угол между диагональю и одной из сторон равен 35 о . Найти угол между диагональю и перпендикуляром, проведенным к этой диагонали.

Н

Задачи на применение теорем

• В прямоугольном треугольнике АВС с острым углом в 30 0 , найти угол между высотой и медианой проведенных из вершины прямого угла к гипотенузе.
• Острые углы прямоугольного треугольника равны 24 о  и 66 о . Найдите угол между высотой и медианой, проведенными из вершины прямого угла.
• Дан прямоугольный треугольник с неравными катетами. Найдите угол между биссектрисой и медианой, если угол между медианой и высотой проведенных к гипотенузе 30 0 .
• Найдите угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, если  А = 31 о ,  В = 59 о .
• Острые углы прямоугольного треугольника равны 29 о и 61 о . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. 
• В треугольнике  АВС  углы  А  и  С  равны 20° и 60° соответственно. Найдите угол между высотой  ВН  и биссектрисой  BD .
• В прямоугольнике угол между меньший стороной и одной из диагонали 30 0 . Найти угол между большей стороной и другой диагональю.
• В прямоугольнике угол между диагональю и одной из сторон равен 35 о . Найти угол между диагональю и перпендикуляром, проведенным к этой диагонали.

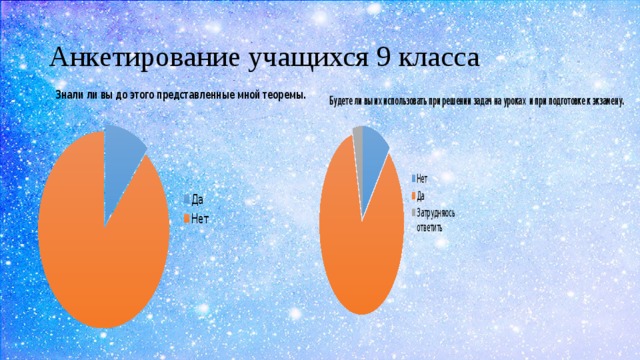
Анкетирование учащихся 9 класса

Заключение

На основании проведённых исследований мы доказали, что некоторые задачи мы можем использовать в качестве теорем. А значит доказали гипотезу, о том, что некоторые задачи, могут оказаться теоремами. Я полностью достигла всех поставленных целей в своем исследовании.

Спасибо за внимание!