Получите свидетельство
Вход
Лекция
Тема: «Пирамида. Усечённая пирамида»
Учебник: Атанасян Л.С., Бутузов В.Ф. Геометрия 10-11 кл.: учебник для общеобразовательных организаций. М: Просвещение, 2016
Цель: сформировать понятия пирамиды, правильной пирамиды, усечённой пирамиды;основания, вершины, боковых рёбер, высоты пирамиды, апофемы правильной пирамиды; площади полной и боковой поверхностей пирамиды.
Сформировать умения: выполнять изображения пирамиды, усечённой пирамиды; находить элементы пирамиды; вычислять площади полной и боковой поверхностей пирамиды. Сформировать умения решать задачи с использованием этих понятий.
План
Пирамида. Правильная пирамида
Усечённая пирамида
Решение задач по теме
1. Пирамида. Правильная пирамида
Пирамидой называется многогранник, одна грань которого – произвольный многоугольник, а другие грани – треугольники, имеющие общую вершину.
| Эти треугольники, имеющие общую вершину, называют боковыми гранями (CPB, BPA, APK и т.д.), их общую вершину – вершиной пирамиды (точка Р). Грань, которая не является боковой, – основанием пирамиды (СВАК…) (рис. 1). В зависимости от фигуры в основании, пирамиды называют треугольные, четырёхугольные, …, n-угольные. На рисунке 1 изображена пятиугольная пирамида. Треугольную пирамиду называют ещё тетраэдром. |
Рис. 1 |
Ребро, не являющееся стороной основания, называют боковым ребром (РС, РВ, РА, РК и т.д.).
Секущая плоскость, которая проходит через боковое ребро и диагональ основания, пересекает пирамиду по треугольнику, который называют диагональным сечением. Треугольная пирамида диагональных сечений не имеет.
Высота пирамиды – это перпендикуляр, опущенный из её вершины на плоскость основания.
Пирамида называется правильной, если её основание – правильный многоугольник, а его центр совпадает с основанием высоты пирамиды.
Все боковые рёбра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой. Ясно, что все апофемы правильной пирамиды равны друг другу. Неправильные пирамиды апофем не имеют.
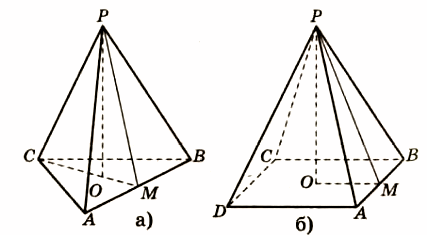
| На рисунке 2 изображены правильные треугольная АВСP и четырёхугольная АВСDP пирамиды. В основании АВС – равносторонний треугольник и АВСD – квадрат. PA, PB, PC, PD – боковые рёбра; РО – высота пирамиды; РМ – апофема пирамиды. |
Рис. 2 |
Теорема
Площадь боковой поверхности правильной пирамиды равна произведению полупериметра её основания на апофему пирамиды:
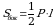
Площадь поверхности пирамиды равна сумме площади её боковой поверхности и площади основания:
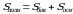
2. Усечённая пирамида
Если произвольную n-угольную пирамиду пересечь плоскостью, параллельной основанию, эта плоскость отсечёт от пирамида многогранник, две грани которого подобные n-угольники, а остальные n граней – трапеции.
Такую часть пирамиды называют усечённой пирамидой. Параллельные грани усечённой пирамиды называют её основаниями, а все другие – боковыми гранями. Высота усечённой пирамиды – это перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания.
Усечённую пирамиду называют правильной, если она является частью правильной пирамиды.
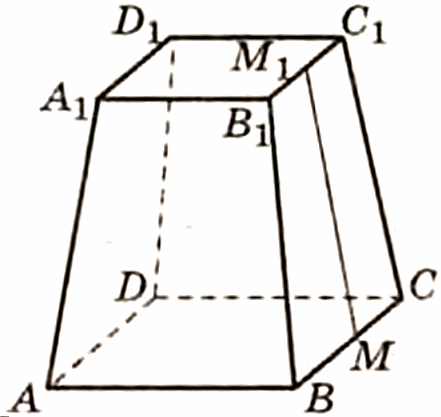
| На рисунке изображена четырёхугольная правильная усечённая пирамида ABCDA1B1C1D1. Грани ABCD и A1B1C1D1 – её основания, М1М – апофема.
|
|
Теорема
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
3. Решение задач по теме
Пример 1. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые рёбра пирамиды, если высота её проходит через точку пересечения диагоналей основания и равна 7 см.
|
| Дано: ABCDP – пирамида, ABCD – ромб, АВ = 5 см, АС = 8 см, РО = 7 см. Найти РА, РВ, РС, РD. |
Решение.
Так как в основании ромб, то РА = РС, РВ = РD.
Рассмотрим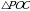 
– прямоугольный, т. к РО – высота, 
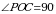. В этом треугольнике РО = 7 см, а 
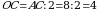см.
По теореме Пифагора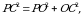 
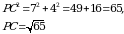
PC = РА =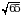 
см.
Рассмотрим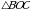 
– прямоугольный, 
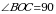(по свойству диагоналей ромба), ВС = 5 см, ОС = 4 см.
По теореме Пифагора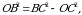 
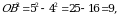
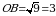см.
Рассмотрим треугольник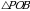 
– прямоугольный, 
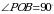, РО = 7 см, ВО = 3 см. По теореме Пифагора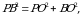 
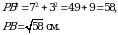
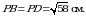
Ответ: PC = РА = 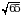см,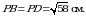
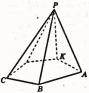
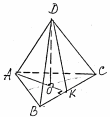
Пример 2. Вычислить площадь боковой поверхности правильной треугольной пирамиды, если её высота равна 4 см, апофема – 8 см.
|
|
Дано: ABCD – правильная триугольная пирамида, AB = ВС = АС. DО = 4 см, АС = 8 см, DК = 8 см. Найти |
.Решение:
Площадь боковой поверхности правильной пирамиды находится по фрмуле: Sбок =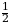 
P·l.
Апофема известна, найдём сторону основания. Рассмотрим ΔODK – прямоугольный, 
DOK=90°, т.к. DO=4 см – высота, DK=8 см. По теореме Пифагора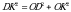 
. Отсюда 
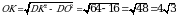(см).
По свойству медиан АО=2ОК=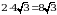
(см).
(см).
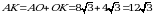Рассмотрим ΔАВK – прямоугольный, АKВ=90°, т.к. АК – высота, медиана и биссектриса в равностороннем треугольнике АВС и ВАK=30°.
; 
; 
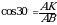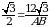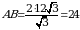(см).
Периметр основания Р=24·3=72 см.
Площадь боковой поверхности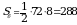 
см2
Ответ: Sб=288 см2
Задача для самостоятельной работы. Основанием пирамиды ABCD является прямоугольный треугольник АВС, у которого гипотенуза АВ равна 29 см, а катет АС равен 21 см. Боковое ребро DА перпендикулярно к плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.
Контрольные вопросы
1. Дайте определение пирамиде.
2. Назовите элементы пирамиды.
3. Что называется высотой пирамиды?
4. Какая пирамида называется правильной?
5. Что такое апофема?
6. Как определить площадь поверхности пирамиды?
7. Какая пирамида называется усеченной?
8. Назовите элементы усеченной пирамиды.
9. Чему равна площадь боковой поверхности правильной усечённой пирамиды?
Конспект лекции "Пирамида. Усеченная пирамида" (994.48 KB)
0
68
0
Нравится
0
