Подборка задач на углы

Подборка задач на смежные и вертикальные углы

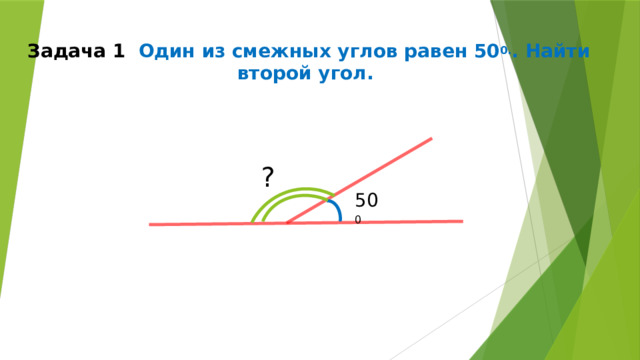
Задача 1 Один из смежных углов равен 50 0. . Найти второй угол.

?

50 0

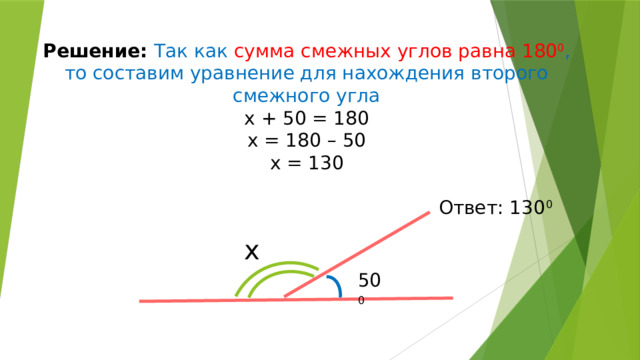
Решение: Так как сумма смежных углов равна 180 0 , то составим уравнение для нахождения второго смежного угла х + 50 = 180 х = 180 – 50 х = 130 Ответ: 130 0

х

50 0

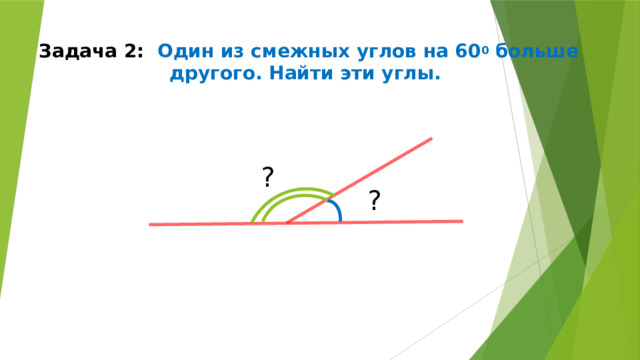
Задача 2: Один из смежных углов на 60 0 больше другого. Найти эти углы.

?

?

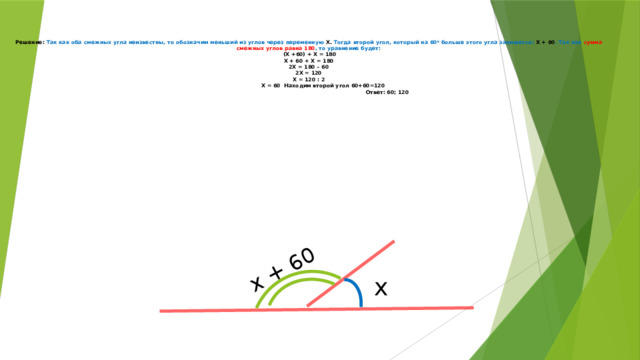
х + 60

Решение: Так как оба смежных угла неизвестны, то обозначим меньший из углов через переменную Х. Тогда второй угол, который на 60 0 больше этого угла запишется: Х + 60 . Так как сумма смежных углов равна 180 , то уравнение будет: (Х +60) + Х = 180 Х + 60 + Х = 180 2Х = 180 – 60 2Х = 120 Х = 120 : 2 Х = 60 Находим второй угол 60+60=120 Ответ: 60; 120

х

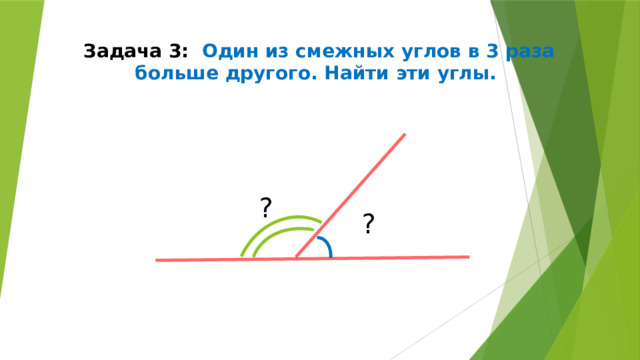
Задача 3: Один из смежных углов в 3 раза больше другого. Найти эти углы.

?

?

Х

3Х

Решение: Величины обоих углов неизвестны. Меньший угол обозначим переменной Х . Так как второй угол в 3 раза больше первого, то величина будет равна 3Х. Сумма смежных углов равна 180 0 , то уравнение принимает вид:

Х + 3Х = 180 0

4Х = 1800

Х = 180 : 4

Х = 45

Меньший угол = 45, а второй 3 * 45 = 135

Ответ: 45; 135

50

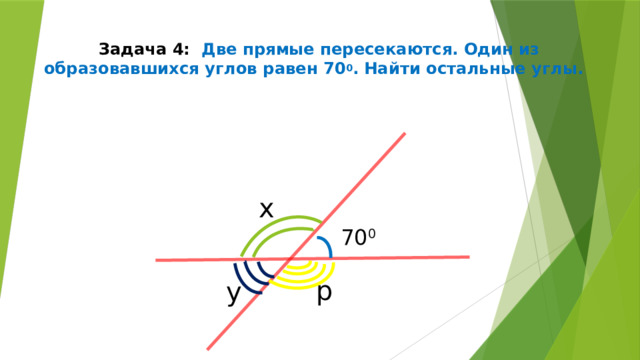
Задача 4: Две прямые пересекаются. Один из образовавшихся углов равен 70 0 . Найти остальные углы.

х

70 0

р

у

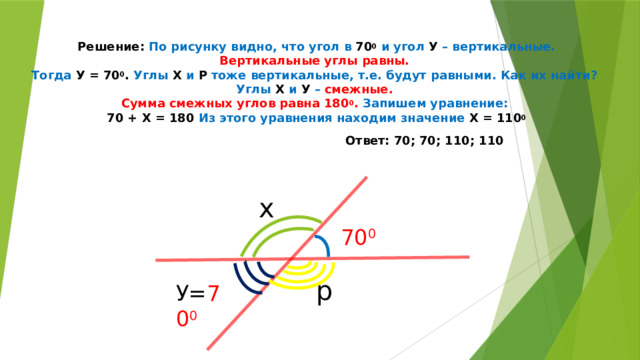
Решение: По рисунку видно, что угол в 70 0 и угол У – вертикальные. Вертикальные углы равны. Тогда У = 70 0 . Углы Х и Р тоже вертикальные, т.е. будут равными. Как их найти? Углы Х и У – смежные. Сумма смежных углов равна 180 0 . Запишем уравнение: 70 + Х = 180 Из этого уравнения находим значение Х = 110 0 Ответ: 70; 70; 110; 110

х

70 0

р

У= 70 0

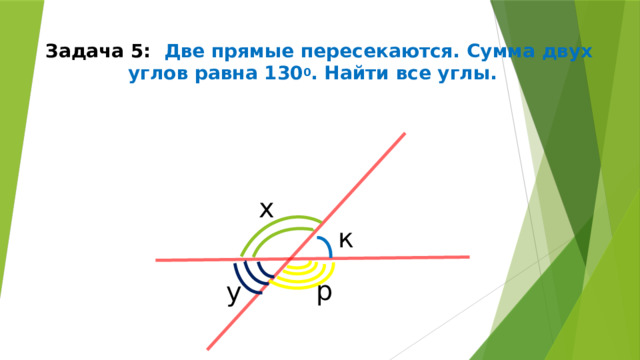
Задача 5: Две прямые пересекаются. Сумма двух углов равна 130 0 . Найти все углы.

х

к

р

у

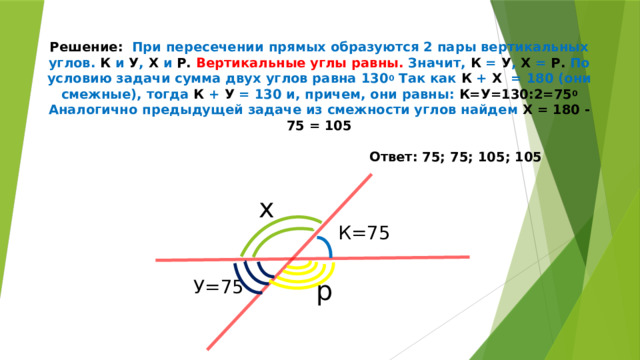
Решение: При пересечении прямых образуются 2 пары вертикальных углов. К и У , Х и Р. Вертикальные углы равны. Значит, К = У , Х = Р. По условию задачи сумма двух углов равна 130 0 Так как К + Х = 180 (они смежные), тогда К + У = 130 и, причем, они равны: К=У=130:2=75 0 Аналогично предыдущей задаче из смежности углов найдем Х = 180 - 75 = 105 Ответ: 75; 75; 105; 105

х

К=75

р

У=75

Спасибо за внимание! Вперед к следующим вершинам Знания!