Тесты на здравый смысл и практическую математику
Давайте задумаемся, каждый на своем месте, в чем же необходимость реформы, что нас не устраивает, чего требует жизнь? Давайте хотя бы для себя разберемся, что в школе главное, попытаемся заложить зерна, которые прорастут в будущем.
Для меня признаки неблагополучия в системе образования следующие:
1. Любознательные по природе дети не хотят учиться.
2. Учителей не хватает ни по количеству, ни по квалификации.
3. Из множества учебников почти нечего выбрать.
4. Нет концепции образования.
5. Есть неудачные попытки реформирования образования.
Не будем обсуждать первичные причины болезни: оплату труда, условия труда, престиж профессии, – это вопросы политики. Поговорим о вторичных причинах, которые менее заметны.
Зачем повышать зарплату тем, кто потерял интерес и квалификацию? Зачем хорошо учить, если дети не хотят учиться? Зачем повышать зарплату, если можно брать деньги с родителей?
Система образования, разрушаясь, как бы усиливает процесс разрушения. Нужна борьба за выживание образования не только путем жалоб или ухода из школы, но и путем формирования позитивного образа школы.
В области математики я вижу первейшую задачу в оживлении курса за счет пересмотра задач, которые должны показывать роль математики и в быту, и в различных профессиях, и для становления логической культуры.
Есть миф о перегрузке школьников, который поставлен во главу угла реформы. На самом деле, детям просто не интересно учиться! Они не понимают, зачем нужны системы уравнений, логарифмы и интегралы.
Я предложил подборки задач, которые, на мой взгляд, должны вернуть школьной математике привлекательность для детей и родителей, такие задачи могут составить конкуренцию кроссвордам.
Есть у меня голубая мечта, чтобы в учебнике математики в каждой теме встретилась хотя бы одна «живая» задача, т.е. задача, которая удовлетворяет хотя бы одному из условий:
1. житейская – связана с повседневной жизнью;
2. занимательная – интересная по сюжету;
3. ключевая – дающая прием решения (базовая, опорная);
4. удивительная – с неожиданным ответом (психологическая);
5. познавательная – несет полезную общекультурную информацию;
6. идейная – оригинальная по решению.
Для характеристики математической подготовки удобно использовать шахматные разряды:
4-й разряд (любитель) – может решать простые одношаговые задачи без уравнений;
3-й разряд (бывалый) – может решать двухшаговые задачи, проявляет смекалку, умеет решать линейные уравнения, понимает проценты;
2-й разряд (опытный) – может проводить цепочки рассуждений и оригинально мыслить;
1-й разряд (тренированный) – умеет переформулировать условие, формулировать леммы;
Кандидат (специалист) – специалист по решению нестандартных задач.
Мастер (профессионал) – профессионал по решению трудных и нестандартных задач.
Тесты на 4-й разряд
(В среднем на задачу надо тратить 1 минуту)
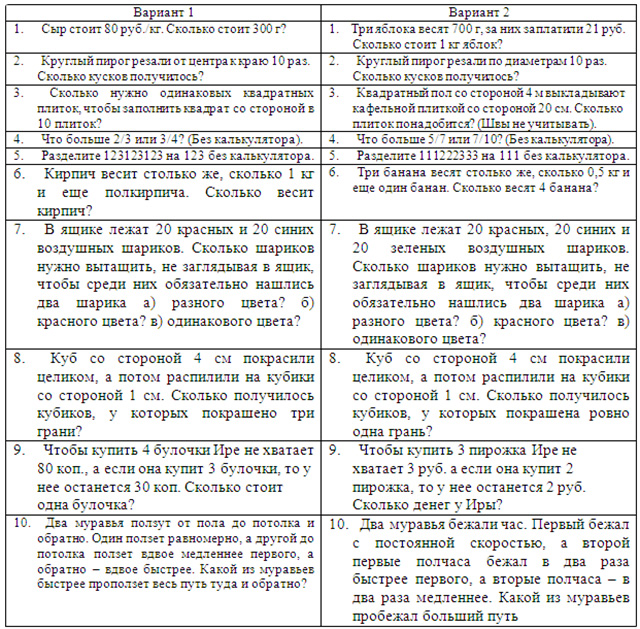
| Вариант 1 | Вариант 2 |
| 1. Сыр стоит 80 руб./кг. Сколько стоит 300 г? | 1. Три яблока весят 700 г, за них заплатили 21 руб. Сколько стоит 1 кг яблок? |
| 2. Круглый пирог резали от центра к краю 10 раз. Сколько кусков получилось? | 2. Круглый пирог резали по диаметрам 10 раз. Сколько кусков получилось? |
| 3. Сколько нужно одинаковых квадратных плиток, чтобы заполнить квадрат со стороной в 10 плиток? | 3. Квадратный пол со стороной 4 м выкладывают кафельной плиткой со стороной 20 см. Сколько плиток понадобится? (Швы не учитывать). |
| 4. Что больше 2/3 или 3/4? (Без калькулятора). | 4. Что больше 5/7 или 7/10? (Без калькулятора). |
| 5. Разделите 123123123 на 123 без калькулятора. | 5. Разделите 111222333 на 111 без калькулятора. |
| 6. Кирпич весит столько же, сколько 1 кг и еще полкирпича. Сколько весит кирпич? | 6. Три банана весят столько же, сколько 0,5 кг и еще один банан. Сколько весят 4 банана? |
| 7. В ящике лежат 20 красных и 20 синих воздушных шариков. Сколько шариков нужно вытащить, не заглядывая в ящик, чтобы среди них обязательно нашлись два шарика а) разного цвета? б) красного цвета? в) одинакового цвета? | 7. В ящике лежат 20 красных, 20 синих и 20 зеленых воздушных шариков. Сколько шариков нужно вытащить, не заглядывая в ящик, чтобы среди них обязательно нашлись два шарика а) разного цвета? б) красного цвета? в) одинакового цвета? |
| 8. Куб со стороной 4 см покрасили целиком, а потом распилили на кубики со стороной 1 см. Сколько получилось кубиков, у которых покрашено три грани? | 8. Куб со стороной 4 см покрасили целиком, а потом распилили на кубики со стороной 1 см. Сколько получилось кубиков, у которых покрашена ровно одна грань? |
| 9. Чтобы купить 4 булочки Ире не хватает 80 коп., а если она купит 3 булочки, то у нее останется 30 коп. Сколько стоит одна булочка? | 9. Чтобы купить 3 пирожка Ире не хватает 3 руб. а если она купит 2 пирожка, то у нее останется 2 руб. Сколько денег у Иры? |
| 10. Два муравья ползут от пола до потолка и обратно. Один ползет равномерно, а другой до потолка ползет вдвое медленнее первого, а обратно – вдвое быстрее. Какой из муравьев быстрее проползет весь путь туда и обратно? | 10. Два муравья бежали час. Первый бежал с постоянной скоростью, а второй первые полчаса бежал в два раза быстрее первого, а вторые полчаса – в два раза медленнее. Какой из муравьев пробежал больший путь |
Тест на 3-й разряд
1. Сколько раз надо пилить поперек трехметровые бревна, чтобы получить 30 чурбаков длиной 1м?
2. Петя 10 раз рубил одно из поленьев на две части и получил 15 тонких поленьев. Сколько поленьев было в начале?
3. В поход идут 10 мальчиков и 15 девочек. Они несут 300кг. Сколько весят рюкзаки мальчика и девочки, если а) мальчик несет на 5 кг больше девочки; б) мальчик несет в 1,5 раза больше девочки?
4. В классе 26 учеников, они едут на экскурсию на автомобилях, в одной машине могут ехать один родитель и четыре школьника. Сколько родителей нужно позвать на экскурсию?
5. Петя говорит Ване: «Если ты дашь мне одного солдатика, то у меня будет солдатиков ровно в два раза больше, чем у тебя». А Ваня отвечает: «Если ты дашь мне одного солдатика, то у нас будет их поровну». Сколько солдатиков было у мальчиков?
6. Сколько букетов получится из 30 белых, 20 розовых и 15 красных гвоздик, если в каждом букете 5 гвоздик всех трех цветов в любом сочетании?
7. Отцу 36 лет, а сыну 12 лет. Через сколько лет отец будет в 2 раза старше сына?
8. Имеется 100 г раствора соли концентрацией 2%. Сколько нужно добавить чистой воды, чтобы концентрация раствора стала 1%?
9. Корова съедает стог сена за 3 дня, а коза – за 6 дней. За сколько дней они съедят стог сена вместе?
10. Контрольную работу назовем легкой, если каждый ученик решил не меньше трех задач. Какая контрольная работа называется нелегкой?
11. Рядовой Петров чистит ведро картошки за 4 часа. За сколько часов он получит полное ведро очищенной картошки, если в очистки уходит 20% картошки?
12. Найдите наименьшее натуральное число, которое делится на любое из чисел 2,3,4,5,6,7,8,9,10.
13. На земле разметили спортивную площадку. Как, не измеряя углов, проверить, является ли она прямоугольником?
14. В некотором царстве среди математиков одна девятая поэтов, а среди поэтов одна десятая математиков. Кого больше в этом царстве: математиков или поэтов?
15. Куб со стороной 4 см покрасили целиком, а потом распилили на кубики со стороной 1 см. Сколько получилось кубиков, у которых а) покрашено ровно 2 грани; б) не покрашено ни одной грани?
16. У Коли есть стенные часы, спешащие на 2 минуты в час, и будильник, отстающий на 1 минуту в час. Вчера Коля поставил правильно и часы, и будильник. Когда он проснулся, стенные часы показывали 7 часов 30 минут, а будильник – 7 часов. Каково было точное время в этот момент?
17. В футбольном турнире участвовало 10 команд. Каждая сыграла с каждой два раза. Сколько было проведено игр?
18. В газете было написано, что в Вифлееме 5 лет назад было 80% христиан и 20 процентов мусульман (других конфессий практически нет). Сейчас число христиан уменьшилось в два раза, а число мусульман увеличилось на 30 тысяч (общая численность населения осталась прежней). Как по этим данным определить, сколько христиан и мусульман сейчас в Вифлееме?
Тест на 2-й разряд
1. Петя распилил несколько бревен на 15 чурбаков, причем сделал 10 распилов. Сколько бревен он распилил?
2. Хозяин обещал работнику за год 12 рублей и кафтан. Но работник ушел через 7 месяцев. При расчете он получил кафтан и 5 рублей. Сколько стоил кафтан?
3. Четыре черные коровы и три рыжих дают за 5 дней столько же молока, сколько три черные коровы и пять рыжих дают за 4 дня. Какая корова дает больше молока в день: черная или рыжая?
4. Кодовый замок имеет три окошка, в каждом окошке можно выставить одну цифру от 0 до 9. Сколько различных кодов можно набрать на этом замке?
5. Два робота за два дня изготовили два компьютера. Сколько компьютеров изготовят 10 роботов за 10 дней?
6. Винни Пух и Пятачок играли в слова (например, кто больше придумает названий рек). Винни Пух придумал 10 слов, а Пятачок только 5. Они называют слова по очереди, причем повторять уже названные слова нельзя. Проигрывает тот, кто при своем ходе не сможет назвать новое слово. Начинает Винни Пух. Придумайте такие слова и такой ход игры, что выиграет Пятачок.
7. В учебнике биологии написано, что каждый волос на голове у человека живет примерно 1500 дней, а потом выпадает. Каждый день выпадает примерно 100 волос и столько же вырастает. Как по этим данным оценить число волос на голове у человека?
8. Одна кастрюля в два раза шире другой при одинаковой высоте. Во сколько раз больше воды в нее поместится?
9. Тормозной путь автомобиля пропорционален квадрату скорости. Известно, что при скорости 40 км/ч тормозной путь равен 3 м. Каким будет тормозной путь при 80 км/ч?
10. В кабинете географии есть карты, глобус, учебники, но нет ответа на вопрос: пролетает ли самолет через озеро Байкал по маршруту Москва-Магадан. Как бы вы поступили?
11. Сколько риса запросил изобретатель шахматной игры? (По легенде на первую клетку надо положить одно рисовое зернышко, на второе – два, и так каждый раз вдвое больше, на последнюю клетку надо положить 263 зерен).
12. Один банк начисляет 2% каждый месяц, а другой банк начисляет 25% каждый год. В какой банк выгоднее положить деньги на год?
13. В типографию привезли рулон бумаги. Как оценить длину бумажной ленты не разворачивая ее?
14. Может ли в пятиугольнике быть четыре острых угла?
15. Верно ли утверждение: «В неравных треугольниках против неравных сторон лежат неравные углы».
16. Как измерить ширину реки не переплывая ее?
17. Двумя ударами топора разрубить подкову на максимальное число частей. Перекладывать части нельзя.
18. Известны данные о температуре по Цельсию и по Фаренгейту: 0С=32F, 10C=50F. Найдите формулу перевода одной шкалы в другую.
19. Бросают две монеты. Что вероятнее: выпадение двух гербов или одного герба и одной цифры?
20. В статье оценивали связь между числом коек в больницах и количеством потребленных лекарств. Оценили параметры уравнения в виде y=ax+b. Получили хорошее соответствие исходным данным и плохие прогнозные свойства модели. Чем это объяснить? (Ответ: модель должна быть вида y=ax).
21. Сколькими способами можно пришить пуговицу, если нитка проходит через все 4 дырочки? а) поворачивать пуговицу нельзя; б) поворачивать пуговицу можно.
Тест на 1-й разряд
1. Сколько чисел, меньших 1000, не делится ни на 2, ни на 3?
2. В полдень часовая и минутная стрелки совпадают. Через какое время они вновь совпадут?
3. Между Волком и Зайцем 100 м. Волк пробегает 100-метровку за 8 секунд, а Заяц – за 10. Через сколько секунд Волк догонит Зайца?
4. Если обычный лист бумаги формата А4 разрезать поперёк на две равные части, то получится лист формата А5, подобный исходному. Чему равно отношение длины листа к его ширине?
5. Свежие грибы содержат по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 220 кг свежих?
6. Пол размером 6×4 м2 надо покрыть плитками размером 20×10 см2. Сколько понадобится плиток, если швы между ними 0,5 см?
7. Сколькими нулями оканчивается произведение 1234…99100?
8. В 2002 г. на среднюю зарплату россиянина можно было купить 300 кг хлеба, либо 150 л молока, либо 20 кг мяса. Почтальон Печкин покупал каждый день 1 кг хлеба, 1 л молока и 0,5 кг мяса. Хватило ли ему средней зарплаты на такое питание на 30 дней?
9. На озере распустилась одна лилия, и каждый день число цветков удваивалось. Через 20 дней все озеро покрылось цветами. За сколько дней покрылась цветами половина озера?
10. Андрей, Борис и Виктор бежали стометровку. Они стартовали одновременно, и каждый бежал с постоянной скоростью. Когда Андрей финишировал, Борису оставалось 10 м, а когда Борис финишировал, то Виктору оставалось 10 м. Сколько метров оставалось Виктору, когда Андрей финишировал?
11. Есть две цилиндрические кружки. Первая вдвое выше второй, зато вторая вдвое шире по диаметру. В какую из кружек больше войдет воды?
12. Почему там, где река узкая – течение быстрое, а там, где река широкая – течение медленное?
13. Продавец привез 200 кг яблок. Скорость продажи V (кг/день) зависит от цены Р (руб./кг) по закону V=104/(P2+100). По какой цене следует продавать яблоки, чтобы а) ожидаемая дневная прибыль была максимальной? б) суммарная прибыль была максимальной, при условии, что яблоки хранятся 10 суток?
14. В билете лотереи за 5 руб. отмечены 6 разных чисел в интервале от 1 до 49. Вам разрешается написать 6 разных чисел в интервале от 1 до 49. Если какие-то три числа у вас и в билете совпадут, то вам выплатят 100 руб. Какова средняя прибыль продавца в расчете на один билет?
15. Можно ли измерить ускорение свободного падения с точностью до 10 знаков после запятой?
16. Высота камня, брошенного от земли вычисляется по формуле h=v0t–gt2/2. При каком v0 камень окажется на высоте 10 м через а) 2 с; б) 3 с? Получим примерно а) 15 м/с; б) 18 м/с. Почему для большего времени нужна большая скорость?
17. Некто собрал данные о среднем душевом доходе во всех семьях города, а затем взял среднее арифметическое этих данных в качестве среднего душевого дохода населения. Верный ли результат он получил? Какой информации не хватает, чтобы правильно посчитать средний душевой доход в городе?
Кандидат в мастера
1. У каждого из n человек появилась своя новость. Они стали посылать друг другу письма, в которых сообщали все известные им к этому моменту новости. Какого наименьшего числа писем хватит, чтобы все узнали все новости?
2. В банку посадили 100 бактерий и один вирус. Каждую минуту вирус поедает одну бактерию, после чего и каждая бактерия и каждый вирус делятся пополам. Сумеют ли вирусы съесть все бактерии?
3. Пол комнаты размером 5х5 м замостили плитками размером 5х20 см, границы которых параллельны стенам. Все щели между плитками и между стенами и плитками нужно обработать. Какова общая длина щелей? (Плитки могут граничить разными по длине сторонами.)
4. Дан клетчатый прямоугольник 10х11. Какое наибольшее число клеток может пересечь (по внутренним точкам) прямая линия?
5. Из чашки с кофе взяли чайную ложку и перелили в чашку с молоком. Затем взяли чайную ложку смеси и перелили в чашку с кофе. Чего больше молока в чашке, где было кофе, или кофе в чашке, где было молоко?
6. У пиратов есть мешок золотого песка и никаких измерительных инструментов. Как им организовать честный дележ, чтобы каждый пират был уверен,
7. Каково наименьшее число гирь, с помощью которых можно набрать любой вес от 1 до 100 г?
Тест на мастера
1. Шах решил испытать 10 своих мудрецов, он объявил, что наденет каждому белый или черный колпак. Каждый будет видеть все колпаки, кроме своего. Кто правильно назовет цвет своего колпака, того прославят, а кто ошибется – прогонят. Мудрецы посовещались и придумали способ называть цвета колпаков, при котором пострадает не более одного мудреца. О чем они могли договориться? А если цветов колпаков k?
2. Танцуют 5 мальчиков и 5 девочек парами (мальчик с девочкой). Может ли так случиться, что каждый из десяти танцующих в каждом следующем танце танцует с более умным или более красивым партнером, а большинство из них танцует и с более умным, и более красивым партнером, чем в предыдущем танце? (Число танцев не ограничено.)
3. Расположите на плоскости несколько точек, чтобы у каждой было ровно 5 точек на расстоянии 1 от нее.
4. Прямоугольник разрезали на прямоугольнички, у каждого из которых есть хотя бы одна целая сторона. Докажите, что у исходного прямоугольника тоже есть хотя бы одна целая сторона.
Тест на гроссмейстера
1. У каждого из n человек появилась своя новость. Они стали звонить друг другу и сообщать все известные им к этому моменту новости. Какого наименьшего числа звонков хватит, чтобы все узнали все новости?
2. Плоскость разрезали вдоль n прямых общего положения (любые три образуют треугольник). Докажите, что среди частей будет не меньше n-2 треугольника.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Тесты на здравый смысл и практическую математику (69.5 КB)
Тесты на здравый смысл и практическую математику (69.5 КB)
 0
0 986
986 37
37 Нравится
0
Нравится
0


