Вагапова Рамиля Радисовна – учитель информатики МБОУ-Гимназия с.Чекмагуш МР Чекмагушевский район РБ
«Трудности, возникшие при подготовке к ГИА
по информатике: разбор отдельных задач»
Государственная итоговая аттестация (ГИА) - это форма государственной оценки освоения выпускниками основных общеобразовательных учебных программ.
Экзамен (ГИА) по информатике является по выбору и состоит из 3-х частей.
Часть 1 содержит 6 заданий базового и повышенного уровней сложности. В этой части собраны задания с выбором ответа, подразумевающие выбор одного правильного ответа из четырех предложенных.
Часть 2 содержит 12 заданий базового и повышенного уровней сложности. В этой части собраны задания с краткой формой ответа, подразумевающие самостоятельное формулирование и запись ответа в виде последовательности символов.
Часть 3 содержит 2 задания высокого уровня сложности. Задания этой части подразумевают практическую работу учащихся за компьютером с использованием специального программного обеспечения. Результатом исполнения каждого задания является отдельный файл. Задание 20 дается в двух вариантах: 20.1 и 20.2; учащийся должен выбрать один из вариантов задания.
Части 1 и 2 выполняются учащимися без использования компьютеров и других технических средств. Вычислительная сложность заданий не требует использования калькуляторов, поэтому в целях обеспечения равенства всех участников экзамена использование калькуляторов на экзаменах не разрешается.
Части 3 выполняются учащимися на компьютере. На компьютере должны быть установлены знакомые учащимся программы. Для выполнения учащимися задания 19 необходима программа для работы с электронными таблицами.
Задание 20 на составление алгоритма дается в двух вариантах по выбору учащегося.
Первый вариант задания (20.1) предусматривает разработку алгоритма для исполнителя «Робот». Для выполнения задания 20.1 рекомендуется использование учебной среды исполнителя «Робот». При отсутствии учебной среды исполнителя «Робот» решение задания 20.1 записывается в простом текстовом редакторе.
Второй вариант задания (20.2) предусматривает запись алгоритма на изучаемом языке программирования (если изучение темы «Алгоритмизация» проводится с использованием языка программирования). В этом случае для выполнения задания необходима система программирования, используемая при обучении.
Рекомендуется проводить экзамен в двух аудиториях. В одной (обычной) аудитории учащиеся выполняют задания частей 1 и 2 на специальных бланках. После исполнения частей 1 и 2 учащиеся сдают бланки работ и переходят в другую аудиторию (компьютерный класс), для выполнения заданий части 3.
Решением каждого задания части 3 является отдельный файл, подготовленный в соответствующей программе (текстовом редакторе или электронной таблице). Учащиеся сохраняют данные файлы в каталог под именами, указанными организаторами экзамена.
Задания в экзаменационной работе оцениваются разным числом баллов в зависимости от их типа и уровня сложности. Выполнение каждого задания части 1 и части 2 оценивается 1 баллом. Выполнение заданий части 3 оценивается от 0 до 2 баллов.
Максимальное количество первичных баллов, которое можно получить за выполнение всех заданий экзаменационной работы, равно 22.
ТРУДНОСТИ ПРИ ПОДГОТОВКЕ К ГИА ПО ИНФОРМАТИКЕ.
Мне кажется, что все, кто занимался подготовкой детей к экзаменам, встречались со следующими общими трудностями:
Незнание содержания материала (не у всех);
Неумение работать с тестовым материалом (не у всех);
Несоответствие содержательного объёма предмета и объёма времени, отводящегося на его освоение;
Зависимость от базовой подготовки выпускников по математике;
Мотивация учащихся;
Отсутствие самостоятельной работы вне школы.
Если говорить о конкретных проблемных темах, то, по моему опыту, они следующие: Системы счисления (перевод); Логические выражения; Работа в ЭТ; Программирование.
При подготовке к ГИА у выпускника появляются новые трудности. Школьнику необходимо предложить самому выбирать задания, с которыми он может справиться. Но ведь это уже очень трудная задача для учащегося, который привык стараться справиться с тем, что задано учителем. К ГИА надо готовиться и по предмету, и психологически. Это связано еще с тем, что задания сформулированы в непривычной для учащегося форме, и кроме того, большинство школьников должны смириться с тем, что все задачи они не решат в отведенное время. Сконцентрироваться надо на понятных для них задачах, решать их спокойно и до конца. Для того, чтобы учащиеся не растерялись перед заданиями и решили правильно больше задач, их нужно готовить не в конце учебного года выпускного класса, а намного раньше – начиная с 5-го класса.
Не существует идеального отчаяния. Каковы бывают отчаяния у учащихся и у учителя после сдачи пробного ГИА? Тот, кто хотел получить высокие баллы - получил низкие, тот, кто был уверен в сдаче - не сдал. У каждого ученика ограничен круг возможностей. Будет неправильно, если во время подготовки не будем учитывать возможности учащегося. Во время осенних каникул можно провести пробный экзамен на школьном уровне и по результатам выявить возможности учащегося и те темы, которые надо повторить с классом. После этого можно разделить класс на 2 группы: 1-ая группа - те, которые просто хотят сдать ЕГЭ, 2-ая группа – те, которые хотят получить средние баллы и которые хотят получить высокие баллы. Когда работаешь с одной группой, другие решают самостоятельно или при помощи сильного ученика. Иногда занимаясь с одной из групп, другая проходит тест в режиме онлайн. Если возникают трудности можно разбирать примеры после уроков. Так же учащиеся могут приходить на индивидуальные занятия после уроков.
По результатам выполнения экзаменационных работ по информатике при проведении государственной (итоговой) аттестации обучающихся, освоивших программы основного общего образования, с участием муниципальных экзаменационных комиссий можно сделать следующие выводы:
у учащихся сложности возникли при решении задании №3 и №4 части 1 (из 9 учащихся не справились с этими заданиями 5);
из части 2 шесть учеников не правильно решили задания №10 и №16;
в части 3 с первым заданием справился только 1 ученик, а со вторым заданием – 2 ученика, что говорит или о нехватке времени, или же о трудностях при решении практических задании.
Рассмотрим задания ГИА, в которых возникли трудности.
№3. Использование информационных моделей (таблицы, диаграммы, графики). Перебор вариантов, выбор лучшего по какому-то признаку.
Что нужно знать:
в принципе, особых дополнительных знаний, кроме здравого смысла и умения перебирать варианты (не пропустив ни одного!) здесь, как правило, не требуется
полезно знать, что такое граф (это набор вершин и соединяющих их ребер) и как он описывается в виде таблицы, хотя, как правило, все необходимые объяснения даны в формулировке задания
чаще всего используется взвешенный граф, где с каждым ребром связано некоторое число (вес), оно может обозначать, например, расстояние между городами или стоимость перевозки
рассмотрим граф (рисунок слева), в котором 5 вершин (A, B, C, D и E); он описывается таблицей, расположенной в центре; в ней, например, число 4 на пересечении строки В и столбца С означает, что, во-первых, есть ребро, соединяющее В и С, и во-вторых, вес этого ребра равен 4; пустая клетка на пересечении строки А и столбца В означает, что ребра из А в В нет


|
| A | B | C | D | Е |
| A |
|
| 3 | 1 |
|
| B |
|
| 4 |
| 2 |
| C | 3 | 4 |
|
| 2 |
| D | 1 |
|
|
|
|
| Е |
| 2 | 2 |
|
|
обратите внимание, что граф по заданной таблице (она еще называется весовой матрицей) может быть нарисован по-разному; например, той же таблице соответствует граф, показанный на рисунке справа от нее
в приведенном примере матрица симметрична относительно главной диагонали; это может означать, например, что стоимости перевозки из В в С и обратно равны (это не всегда так)
желательно научиться быстро (и правильно) строить граф по весовой матрице и наоборот
Пример. Между населенными пунктами А, В, С, D, Е построены дороги, протяжённость которых приведена в таблице

Определите кратчайший путь между пунктами A и D (при условии, что передвигаться можно только по построенным дорогам).
1) 6 2) 7 3) 8 4) 9
Решение:
Дана, так называемая, матрица (в задании — таблица). Рисуем граф.
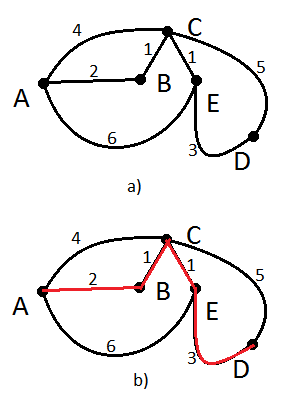
Перебрав комбинации путей между пунктами А и D, можно определить самый короткий, обозначенный красным цветом на рисунке.

А - B - C - E - D = 2+1+1+3 = 7
Ответ: 2) 7.
Возможные ловушки и проблемы:
можно не заметить, что маршруты, проходящие через большее число пунктов, оказываются короче (A-B-C короче, чем A-C, A-B-C-E короче, чем A-E)
№4. Файловая система. Работа с файлами и каталогами (папками).
Пример.
Пользователь работал с каталогом Участники. Сначала он поднялся на один уровень вверх, затем спустился на уровень вниз, потом ещё раз спустился на один уровень вниз.
В результате он оказался в каталоге
С:\Конференция\Секции\Информатика
Запишите полный путь каталога, с которым пользователь начинал работу.
1) С:\Конференция\Регионы\Списки\Участники
2) С:\Конференция\Участники
3) С:\Конференция\Регионы\Участники
4) С:\Участники
Решение:
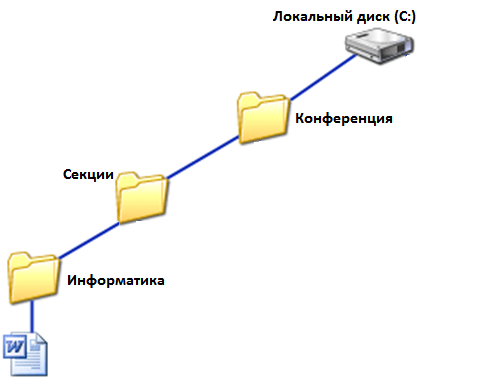
Чтобы найти решение, можно пойти от обратного.
Вверх на два уровня от каталога «Информатика» и вниз на один в каталог «Участники»
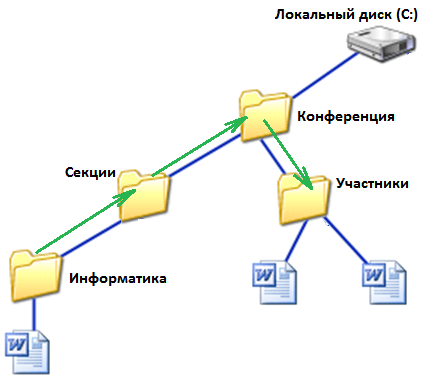
Ответ:
2) С:\Конференция\Участники
№10. Исполнение циклического алгоритма обработки массива чисел, записанного на языке программирования.
Пример.
В таблице Dat хранятся данные измерений среднесуточной температуры за неделю в градусах (Dat[1] – данные за понедельник, Dat[2] – за вторник и т.д.). Определите, что будет напечатано в результате выполнения следующего алгоритма, записанного на трех алгоритмических языках.
(на языке Паскаль)
Var k, m, day: integer;
Dat: array[1..7] of integer;
Begin
Dat[1]:=14; Dat[2]:=10;
Dat[3]:=0; Dat[4]:=15;
Dat[5]:=0; Dat[6]:=15;
Dat[7]:=10;
day:= 1; m:=Dat[1];
for k:=2 to 7 do begin
if Dat[k] m then begin
m:=Dat[k]; day:=k
end;
end;
write(day);
End.
Ответ: 4
№16.
Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Сначала вычисляется длина исходной цепочки символов; если она чётна, то в середину цепочки символов добавляется символ А, а если нечётна, то в начало цепочки добавляется символ Б. В полученной цепочке символов каждая буква заменяется буквой, следующей за ней в русском алфавите (А – на Б, Б – на В и т. д., а Я – на А).
Получившаяся таким образом цепочка является результатом работы алгоритма.
Например, если исходной была цепочка ВРМ, то результатом работы алгоритма будет цепочка ВГСН, а если исходной была цепочка ПД, то результатом работы алгоритма будет цепочка РБЕ.
Дана цепочка символов ПУСК. Какая цепочка символов получится, если к данной цепочке применить описанный алгоритм дважды (т. е. применить алгоритм к данной цепочке, а затем к результату вновь применить алгоритм)?
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Решение:
Напишем условие кратко:
Длина четная: в середину А,
Нечетная: в начало Б.
Каждая буква заменяется буквой, следующей за ней.
ПУСК
Длина чет., значит ПУАСК, далее заменяем каждую букву на последующую и получим РФБТЛ.
Повторим еще раз.
Длина нечет., значит БРФБТЛ, далее заменяем каждую букву на последующую и получим ВСХВУМ.
Ответ: ВСХВУМ
№19
В электронную таблицу занесли результаты тестирования учащихся по русскому языку и математике. На рисунке приведены первые строки получившейся таблицы.
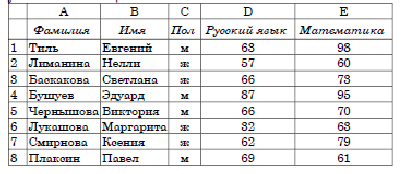
В столбце A указана фамилия учащегося, в столбце B – имя учащегося, в столбце C – пол учащегося, в столбцах D, E – баллы, полученные соответственно по русскому языку и математике. По каждому предмету
можно было набрать от 0 до 100 баллов. Всего в электронную таблицу были занесены данные по 1000 учащимся. Порядок записей в таблице произвольный.
Выполните задание.
Откройте файл с данной электронной таблицей (расположение файла Вам сообщат организаторы экзамена). На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
1. Чему равен средний балл по математике среди девочек? Ответ с точностью до одного знака после запятой запишите в ячейку G1 таблицы.
2. Сколько процентов от общего числа участников составили ученики, набравшие более 50 баллов по русскому языку? Ответ запишите в ячейку G2 таблицы.
Полученную таблицу необходимо сохранить под именем, указанным организаторами экзамена.
Решение:
Данную задачу можно решать разными способами. Приведем один из них.
В столбце F для каждой учащейся (напротив фамилии в поле "Пол" указано значение "ж") запишем значение балла по математике. В ячейку F2 запишем формулу =ЕСЛИ(C2="ж"; E2;"")
Скопируем формулу во все ячейки диапазона F3:F1001. Благодаря использованию относительных ссылок в столбце F в строках 2–1001 будут записаны суммы учеников - девочек. Теперь в дополнительной ячейке, например H3 посчитаем количество девочек по формуле =СЧЁТЕСЛИ(C2:C1001;"ж")
Для того чтобы найти средний балл, в ячейку G1 внесём формулу =СУММ(F2:F1001)/H3
Для ответа на второй вопрос запишем в ячейке G2 формулу =СЧЁТЕСЛИ(D2:D1001;"50")/1000 и сделаем формат ячейки процентным.
Возможны и другие способы решения задачи.
Если задание выполнено правильно и при выполнении задания использовались файлы, специально подготовленные для проверки выполнения данного задания, то должны получиться следующие ответы:
на первый вопрос – 67,8;
на второй вопрос – 87.
№20.1.
Пример.
Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Ниже приведено описание Робота. У Робота есть четыре команды перемещения:
вверх
вниз
влево
вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. Если Робот получит команду передвижения через стену, то он разрушится.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится Робот:
сверху свободно
снизу свободно
слева свободно
справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если то
последовательность команд
все
«Последовательность команд» – это одна или несколько любых команд, выполняемых Роботом. Например, для передвижения на одну клетку вправо, если справа нет стенки, можно использовать такой алгоритм:
если справа свободно то
вправо
все
В одном условии можно использовать несколько команд, применяя логические связки и, или, не, например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Также у Робота есть команда закрасить, закрашивающая клетку, в которой Робот находится в настоящий момент.
Выполните задание. На бесконечном поле имеется горизонтальная стена. Длина стены неизвестна. От правого конца стены вниз отходит вертикальная стена также неизвестной длины. Робот находится в клетке, расположенной над горизонтальной стеной.
Н а рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
а рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные правее вертикальной стены и клетку в месте соединения вертикальной и горизонтальной стен. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
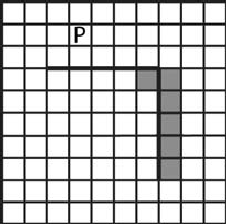
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться.
Алгоритм напишите в текстовом редакторе и сохраните в текстовом файле. Название файла и каталог для сохранения Вам сообщат организаторы экзамена.
Решение:
Команды исполнителя будем записывать жирным шрифтом, а комментарии, поясняющие алгоритм и не являющиеся его частью, – курсивом. Начало комментария будем обозначать символом «|».
| Двигаемся вниз, пока не дойдём до горизонтальной стены,
нц пока снизу свободно
вниз
кц
| Двигаемся вправо, пока не дойдём до конца горизонтальной стены,
нц пока не снизу свободно
вправо
кц
| Двигаемся вниз, пока не дойдём до конца вертикальной стены,
закрашиваем клетки
вниз
нц пока не слева свободно
закрасить
вниз
кц
| Переместимся в нижнюю клетку слева от вертикальной стены
влево
| Двигаемся вверх до горизонтальной стены, закрашиваем клетку в месте
соединения стен
нц пока сверху свободно
вверх
кц
закрасить
Возможны и другие варианты решения
№20.2.
Напишите программу, которая вычисляет произведение членов последовательности, кратных 5. Программа получает на вход целые числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 – признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000.
Программа должна вывести одно число: произведение членов последовательности, кратных 5.
Пример работы программы:

Решением является программа, записанная на любом языке программирования.
Решение:
var a, P: integer;
begin
readln(a);
P:=1;
while a0 do
begin
if (a mod 5=0) then P:=P*a;
readln(a);
end;
writeln(P);
end.
Возможны и другие варианты решения.
Решение трудностей, возникшие при подготовке к ГИА во многом зависит от возможностей самих учащихся. Можно попробовать следующее:
Разделение учащихся по уровню подготовки на группы.
Блочное рассмотрение материала (от теории к решению задач, от простого к сложному, от стандартных задач до усложненных примеров и ЕГЭ);
Подбор учителем необходимых заданий для тренинга в электронном и бумажном варианте.
Отработка внимательного, неторопливого и вдумчивого чтения заданий и такого же выполнения арифметических вычислений.
Разбор решений непохожих друг на друга заданий.
Тестирование по форме ЕГЭ в конце каждого блока и смежных блоков;
(апрель, май – постоянное прорешивание тестов и устранение неясностей в решении задач)
Обязательная самостоятельная (домашняя) работа учащихся, проверяемая учителем.
Дополнительные индивидуальные, при необходимости, консультации.
При этом необходимо использовать материалы соответствующих сайтов и печатных изданий для подготовки к ЕГЭ и ГИА.


 Получите свидетельство
Получите свидетельство Вход
Вход










 а рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
а рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).










 Статья для учителей информатики "Трудности, возникшие при подготовке к ГИА: разбор отдельных задач" (0.28 MB)
Статья для учителей информатики "Трудности, возникшие при подготовке к ГИА: разбор отдельных задач" (0.28 MB)
 0
0 2043
2043 180
180 Нравится
0
Нравится
0


