Учитель берёт понравившееся ему высказывание или слова из песни, стихотворения, пословицу.
По количеству букв в этом высказывании подбирается столько же примеров и задач так, чтобы одинаковым буквам соответствовали одинаковые ответы.
Игра занимает 10-12 минут, иногда меньше. Каждому ученику учитель даёт карточку и ученик сразу начинает решать.
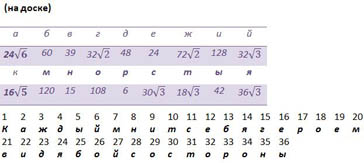
На доске записаны буквы, которые встречаются в высказывании, и под ними ответы, которые соответствуют этим буквам.
Ниже записаны числа по порядку (по количеству букв в высказывании).
Ученик, выполнивший задание, называет номер своей карточки и букву, под которой записан ответ. И так далее. Ученики стараются быстрее решить, чтобы получить следующую карточку.
За правильно решенные 2-3 задания он может получить оценку. Поэтому желательно карточек иметь больше, чем число учеников в классе.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход


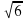
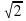
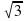
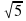
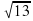 , один из его катетов равен 10.
, один из его катетов равен 10.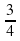 длины средней линии.
длины средней линии.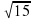 .
.








 Площади параллелограмма, треугольника, трапеции (19.77 КB)
Площади параллелограмма, треугольника, трапеции (19.77 КB)
 0
0 1033
1033 62
62 Нравится
0
Нравится
0




