Цель и задачи урока:
- выработать у учащихся навыки применения формул площади фигур при решении задач, уметь выделять главное из теорем и определений, делать выводы;
- развивать знания, умения и навыки учащихся при решении задач, формировать вычислительные навыки и математическую грамотность учащихся ;
- прививать интерес к предмету.
Ход урока.
I. Организационный момент.
II. Доклады об ученых – геометрах.
1. доклад о Евклиде;
2. доклад о Пифагоре;
3. доклад о Героне.
III. Аукцион по продаже «пятерок».
Учитель читает вопрос, делает ошибку, желающие отвечать, поднимают руку, исправляют ошибку.
1) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
2) Треугольники подобны у которых соответственные стороны пропорциональны
3) Центр окружности, вписанной в треугольник является точка пересечения его медиан (биссектрис).
4) Для подобия двух прямоугольных треугольников достаточно, чтобы у них было по равному острому углу катету.
5) В треугольнике против большего угла лежит меньшая (большая) сторона.
IV. Аукцион по продаже треугольника.
Вопросы:

1. Что называется треугольником?
2. Виды треугольников?
3. Назовите основные элементы треугольника.
4. Определение биссектрисы треугольника.
5. Определение медианы треугольника.
6. Определение высоты в треугольнике.
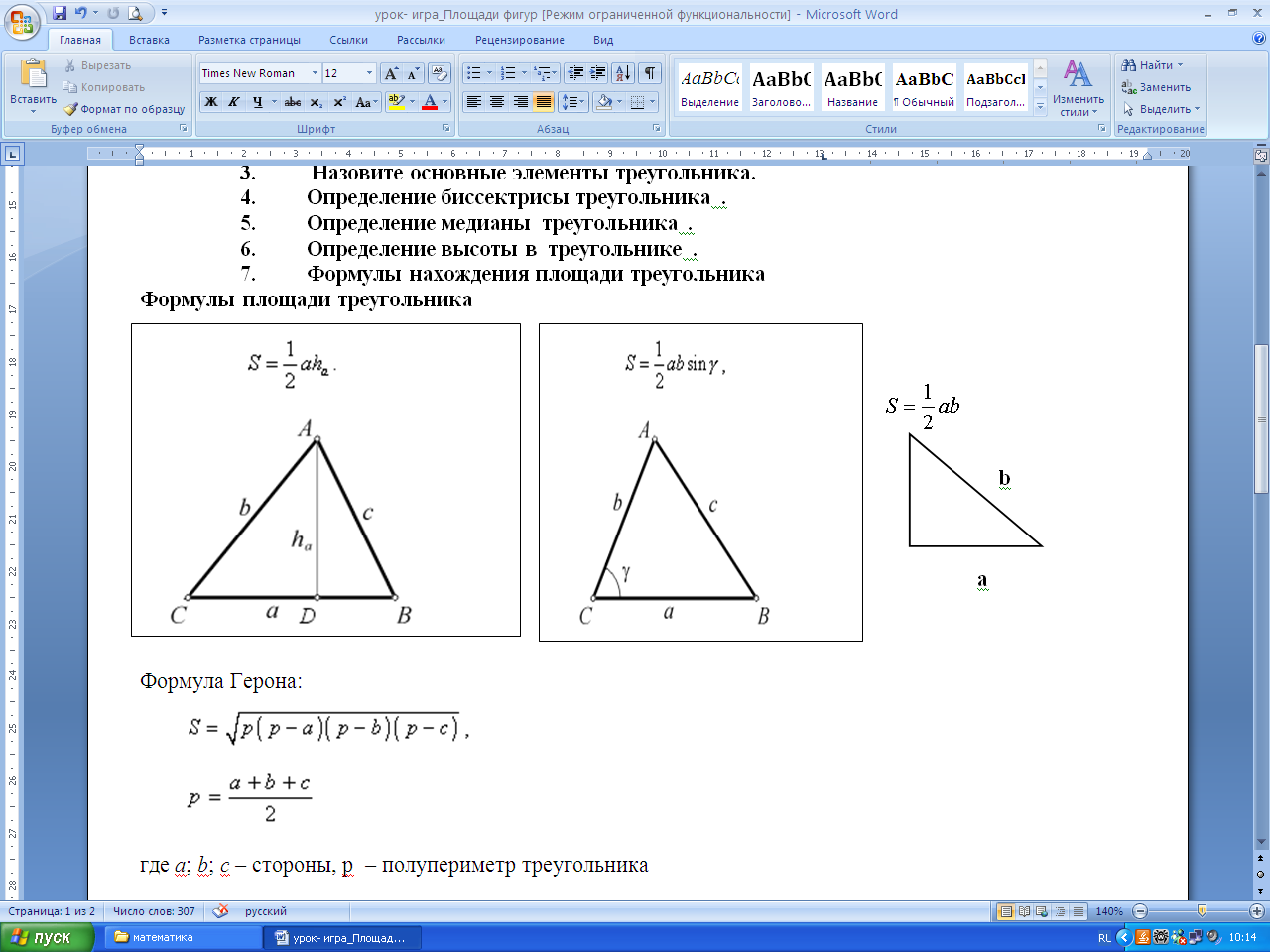
7. Формулы нахождения площади треугольника
Формулы площади треугольника.
8. Соотношения между сторонами и углами в прямоугольном треугольнике
V. Аукцион по продаже параллелограмма.
1. Что называется параллелограммом?
2. Свойства диагоналей параллелограмма.
3. Свойство противоположных сторон и углов параллелограмма
4. Что называется ромбом? Свойства диагоналей ромба
5. Формула площади ромба
6. Формула площади параллелограмма
VI. Практическая работа.
(Задачи на нахождение площади треугольника, ромба, параллелограмма)
1. Площадь прямоугольника равна 24. Найдите площадь прямоугольника с вершинами в серединах сторон прямоугольника.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


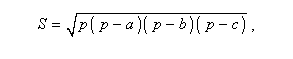
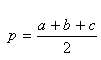









 Площади фигур (конспект) (0.21 MB)
Площади фигур (конспект) (0.21 MB)
 0
0 776
776 69
69 Нравится
0
Нравится
0









