Цели и задачи урока:
Уточнить и расширить представление о прямоугольном параллелепипеде как о пространственной фигуре.
Сформировать способность к применению формулы объёма прямоугольного параллелепипеда.
Повторить решение задач с использованием формул площади и периметра прямоугольника и квадрата.
Тренировать умение решать примеры на умножении и деление круглых чисел.
Тренировать умение решать практические задачи, производить измерения.
Развивать мыслительные операции: сравнение, анализ, классификация, пространственного воображения.
Развивать культуру математической речи и эмоций учащихся, наблюдательности и любознательности, развитию познавательной активности, формированию навыков работы в группах.
Сформировать способность выдвигать гипотезы, анализировать, сравнивать, строить доказательства, обосновывать выводы.
Предполагаемые результаты деятельности учащихся на уроке:
Личностные результаты
Принятие социальной роли ученика, осознание личностного смысла учения и интерес к изучению математики.
Развитие самостоятельности и личной ответственности за свои поступки, способность к рефлексивной самооценке собственных действий .
Освоение норм общения и коммуникативного взаимодействия, навыков сотрудничества со взрослыми и сверстниками, умение находить выходы из спорных ситуаций.
Мотивация к работе на результат как в исполнительской, так и в творческой деятельности.
Установка на здоровый образ жизни, спокойное отношение к ошибке как рабочей ситуации, требующей коррекции, вера в себя.
Метапредметные результаты
Умение выполнять пробное учебное действие, в случае его неуспеха грамотно фиксировать своё затруднение, анализировать ситуацию, выявлять и конструктивно устранять причины затруднения.
Освоение начальных умений проектной деятельности: постановка и сохранение целей учебной деятельности, определение наиболее эффективных способов и средств достижения результата, планирование, прогнозирование, реализация построенного проекта.
Умение контролировать и оценивать свои учебные действия на основе выработанных критериев в соответствии с поставленной задачей и условиями её реализации.
Приобретение опыта использования методов решения проблем творческого и поискового характера.
Освоение начальных форм познавательной и личностной рефлексии.
Способность к использованию знаково-символических средств математического языка и средств ИКТ для описания и исследования окружающего мира (для представления информации, создания моделей изучаемых объектов и процессов, решения коммуникативных и познавательных задач и др.) и как базы компьютерной грамотности.
Формирование специфических для математики логических операций(сравнение, анализ, синтез, обобщение, классификация, аналогия, установление причинно-следственных связей, построение рассуждений, отнесение к известным понятиям), необходимых человеку для полноценного функционирования в современном обществе; развитие логического, эвристического и алгоритмического мышления.
Освоение норм коммуникативного взаимодействия в позициях «автор», «критик», «понимающий», готовность вести диалог, признавать возможность и право каждого иметь своё мнение, способность аргументировать свою точку зрения.
Умение работать в парах и группах, договариваться о распределении функций в совместной деятельности, осуществлять взаимный контроль, адекватно оценивать собственное поведение и поведение окружающих; стремление не допускать конфликты, а при их возникновении готовность конструктивно их разрешать.
Начальные представления о сущности и особенностях математического знания, его обобщённого характера и роли в системе знаний.
Освоение базовых предметных и межпредметных понятий (алгоритм, множество, классификация и др.).
Умение работать в материальной и информационной среде начального общего образования (в том числе с учебными моделями) в соответствии с содержанием учебного предмета «Математика».
Предметные результаты
Освоение опыта самостоятельной математической деятельности по получению нового знания, его преобразованию и применению для решения учебно-познавательных и учебно-практических задач.
Использование приобретённых математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также оценки их количественных и пространственных отношений.
Овладение устной и письменной математической речью, основами логического, эвристического и алгоритмического мышления, пространственного воображения, счёта и измерения, прикидки и оценки, наглядного представления данных и процессов (схемы, таблицы, диаграммы, графики), исполнения и построения алгоритмов.
Умение выполнять устно и письменно арифметические действия с числами, составлять числовые и буквенные выражения, находить их значения, решать текстовые задачи, исполнять и строить алгоритмы, составлять и исследовать простейшие формулы, распознавать, изображать и исследовать геометрические фигуры, работать с таблицами, схемами, представлять, анализировать и интерпретировать данные.
Приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач.
Оборудование: презентация к уроку, интерактивная доска, проектор, модели кубов и параллелепипедов, модель параллелепипеда, закреплённая на вершине, модели параллелепипедов, закреплённые на ребрах.
Раздаточный материал: модели параллелепипедов единого размера, изготовленных детьми на уроках технологии; модели кубов единого размера;
памятки с формулами нахождения периметра, площади, сторон прямоугольника и квадрата, нахождения объёма параллелепипеда, переместительного и сочетательного свойства умножения; карточки для построения параллелепипеда.
Ход урока
Учитель: Здравствуйте, ребята! Садитесь.
Учитель: А, знаете ли вы что на свете всего быстрее? Быстрее звука, быстрее света?
Дети: (высказывают предположения 3-5) Человеческая мысль.
Учитель: Желаю вам сегодня работать со скоростью мысли и не отставать от своих товарищей.
Учитель: Какие средства и ваши личностные качества в этом помогут?
Дети: Знания, внимательность, сосредоточенность, умение анализировать, делать выводы, строить доказательства и т.д.
Учитель: Прочитайте слова эпиграфа:
Дети: «Математику нельзя изучать, наблюдая, как это делает сосед». А.Нивен
Учитель: Как вы понимаете высказывание Нивена?
Дети: Надо самому трудиться, добывать знания, а не смотреть на соседа.
Учитель: Как ты будешь изучать математику?
Дети: Я сам буду изучать, тогда все будет понятно и просто.
Учитель: Замечательно! Кто нам сегодня поможет?
Учитель: Какое знание вам понадобилось для выполнения домашней работы?
Дети: Знание формул нахождения площади и периметра прямоугольника.
Учитель: Что такое формулы?
Дети: Это верные равенства, устанавливающие взаимосвязь между величинами.
Учитель: У кого возникли затруднения? (Проверка по эталону).
Учитель: Вы молодцы, справились с заданием!
Учитель: Как ты думаешь, мы изучили все формулы. Дети: Нет.
Учитель: Для чего нужны формулы?
Дети: Они помогают при решении задач.
Учитель: ВЫ готовы решать задачи, используя своё знание формул?
Дети: ДА!
Учитель: Молодцы! Теперь это знание поможет нам еще раз. Используя формулы, вы узнаете, что мы будем изучать сегодня на уроке.
Учитель: Считаем устно. Найдите на карточке среди предложенных чисел правильный ответ. Соедините ответы последовательно по линейке.
Давая ответ на задачу, необходимо найти на доске и проговорить формулу, по которой ты действовал.
Задачи:
Учитель: 1)(2 ·19)· 5= (190)
Дети: (а · b)· c= a· (b· c) –сочетательное свойство умножения
Учитель: 2)Площадь прямоугольника со сторонами 9м и 40м Дети: Дети: (360м2 ). Sпр. = a · b – Чтобы найти площадь прямоугольника, надо перемножить длины его сторон.
Учитель: 3)Периметр квадрата со стороной 12м (48м).
Дети: Pкв .= a · 4 – Чтобы найти периметр квадрата, надо длину стороны умножить на 4.
Учитель: 4)Площадь квадрата со стороной 5см (25см2).
Дети: Sкв. = a · а. – Чтобы найти площадь квадрата, надо перемножить длины двух сторон. (Соединить с первой точкой, продолжить от первой точки 190.)
Учитель: 5)Сторону прямоугольника, другая сторона которого равна 20м, а площадь -180м2 (9м).
Дети: апр. = S : b – Чтобы найти длины стороны прямоугольника, надо площадь разделить на длину известной стороны.
Учитель: 6)Сторону квадрата, периметр которого 160см (40см).
Дети: а = Р : 4 – Чтобы найти сторону квадрата, надо периметр разделить на 4.
Учитель: 7)Периметр прямоугольника со сторонами 23см и 27см (100см).
Дети: Pпр. = (a+b) ·2 (Соединить с точкой 48м)
Учитель: Что просматривается по точкам?
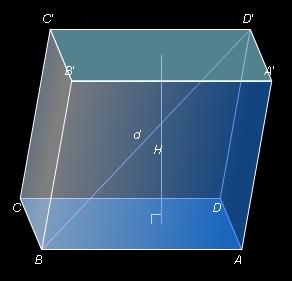
Дети: Прямоугольный параллелепипед.
Учитель: 8)Все ли точки мы нашли?
Дети: Последнюю точку вы уже угадали?
Дети: Да – 36!
Учитель: Тогда проверьте себя. Найдите объём параллелепипеда, длина которого 6 дм, ширина 2 дм, а высота 3дм.
Дети: 36дм3 !
Учитель: Сформулируйте, как найти объём параллелепипеда?
Дети: Надо площадь основания умножить на высоту.
Учитель: Посмотрите на рисунок. Какая фигура здесь лишняя? Почему?
Дети: Прямоугольник лишний, т.к. он фигура плоская
Учитель: Модели параллелепипедов есть у вас на партах. Сколько их?
Дети:3, 1из них куб.
Учитель: Что обозначено на слайде рыжими точками?
Дети: Вершины параллелепипеда.
Учитель: Сколько у параллелепипеда вершин? Дети: 8.
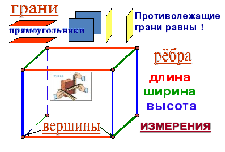
Учитель: Что показано разными цветами? Дети: Рёбра.
Дети: Красным цветом – длина - 4;
Зелёным – ширина - 4;
Синим – высота - 4.
Учитель: Сколько всего рёбер? Дети:- 12.
Учитель: Сколько измерений необходимо произвести, чтобы начертить прямоугольный параллелепипед?
Дети: Три.
Учитель: Сколько ребер выходит из одной вершины? Дети: Три.
Учитель: В чем их особенность?
Дети: Они разного цвета, значит, разной длины.
Учитель: Как можно назвать длину, высоту и ширину одним словом? Дети: (Измерения)
Учитель: Сколько различных измерений у параллелепипеда? Дети:- 3!
Учитель: Как назовут пространственную фигуру, у которой все ребра будут равными? Дети: Куб.
Учитель: Как называются «стороны» параллелепипеда? Дети: Грани.
Учитель: Сколько граней? Дети: 6.
Учитель: А сколько пар граней? Дети: 3.
Учитель: ЧТО представляют собой грани?
Дети: Прямоугольники.
Учитель: Каковы особенности куба?
Дети: Равные рёбра, равные грани – квадраты.
Учитель: Можно ли вычислить площадь граней параллелепипеда, зная длину, ширину и высоту? Как?
Дети:
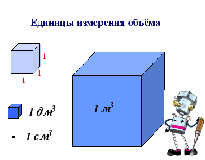
Учитель: Чем ещё характеризуется пространственная фигура? Дети: ОБЪЁМОМ.
Учитель: Какие меры для измерения объёма вы знаете? Дети: мм3, дм3, м3, см3 , ЛИТР - для жидкостей.
Весь конспект урока - смотрите архив.

 Получите свидетельство
Получите свидетельство Вход
Вход





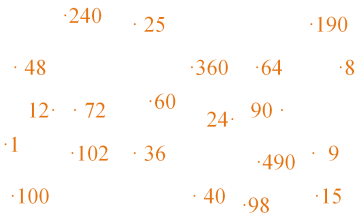







 (10·7)·4= (7·4)·10= (10·4)·7=280(см3)
(10·7)·4= (7·4)·10= (10·4)·7=280(см3) 
 высота
высота










 Формула объёма прямоугольного параллелепипеда (3.6 MB)
Формула объёма прямоугольного параллелепипеда (3.6 MB)
 0
0 2404
2404 242
242 Нравится
0
Нравится
0











