Пирамида. Основные элементы. Площади поверхностей. Объем.

Тема:

Пирамида

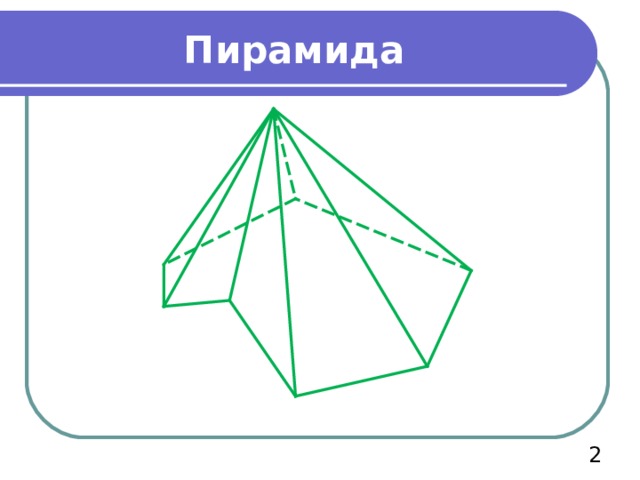
Пирамида

Призма

Додекаэдр

Икосаэдр

Курносый куб

Пирамида - это многогранник, составленный из n – угольника и n треугольников, имеющих общую вершину

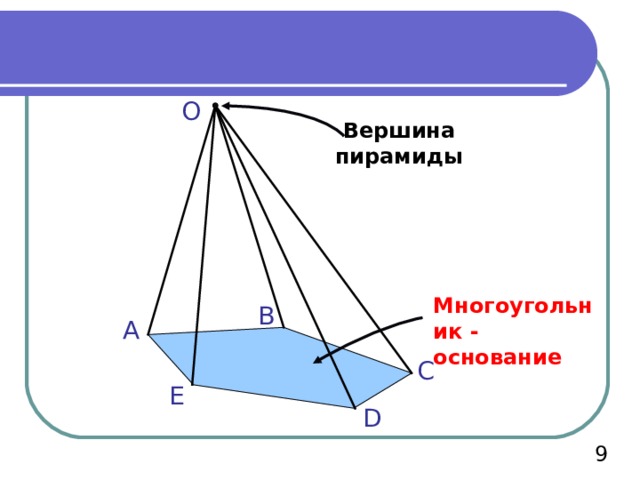
O

Вершина пирамиды

Многоугольник - основание

В

А

С

E

D

9

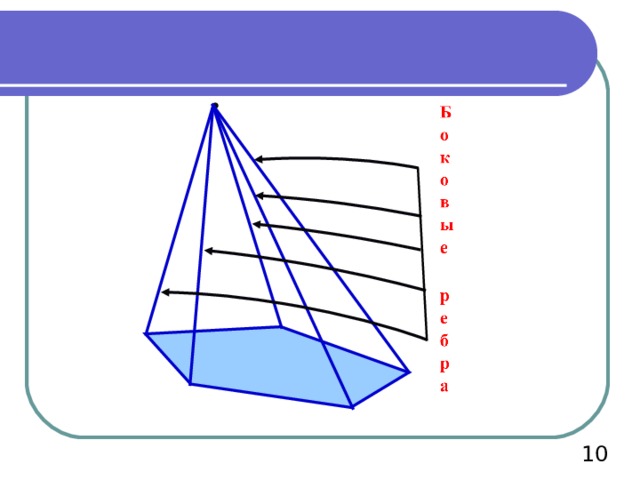
9

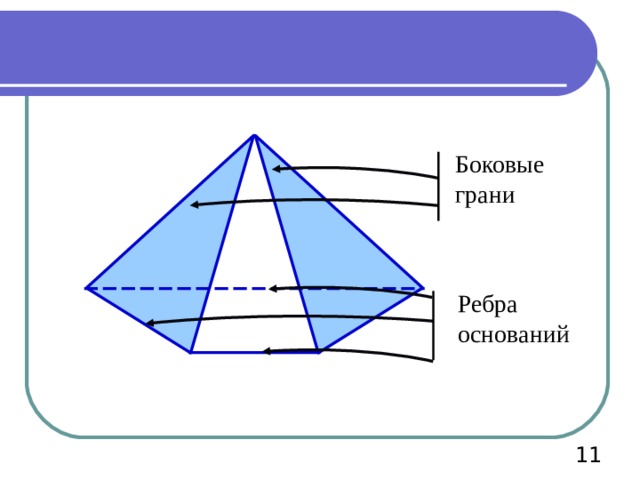
Боковые грани

Ребра оснований

11

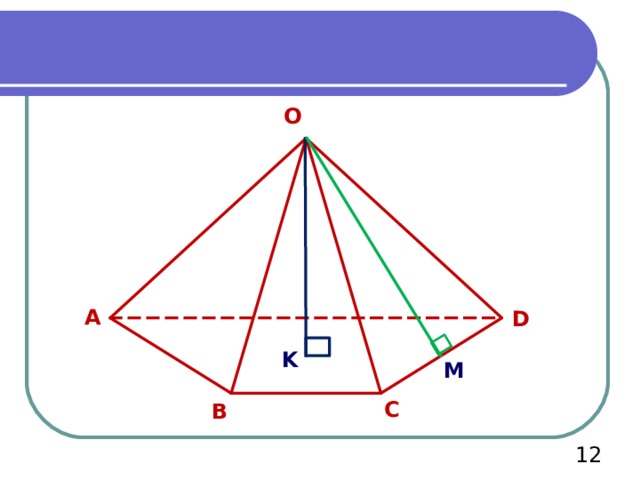
O

A

D

K

M

C

B

11

Пирамида называется правильной, если ее основание — правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания (ОК), является ее высотой.

12

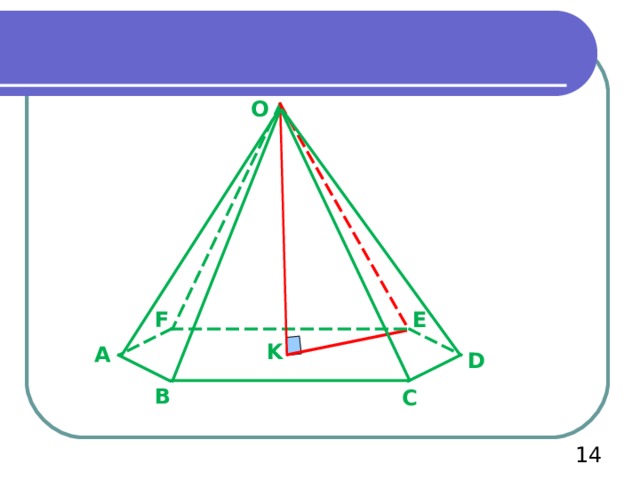
O

F

E

K

A

D

B

C

12

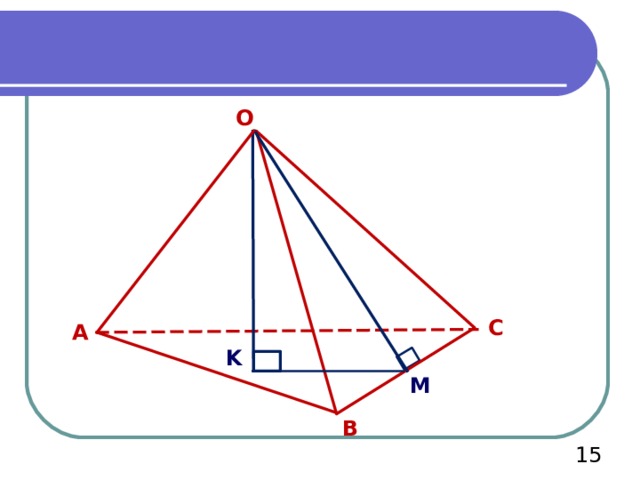
O

C

A

K

M

B

14

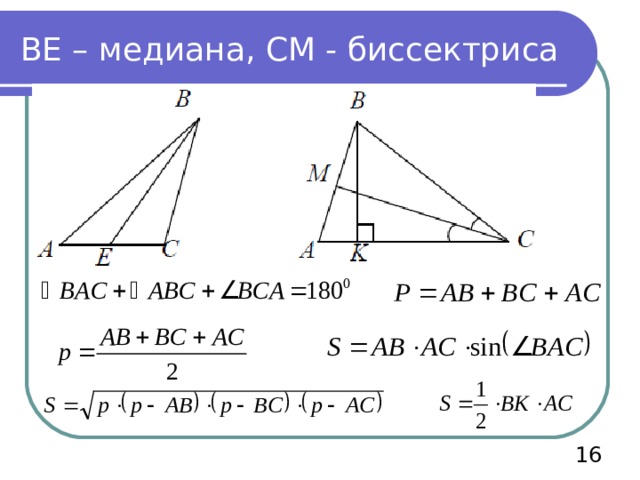
ВЕ – медиана, СМ - биссектриса

15

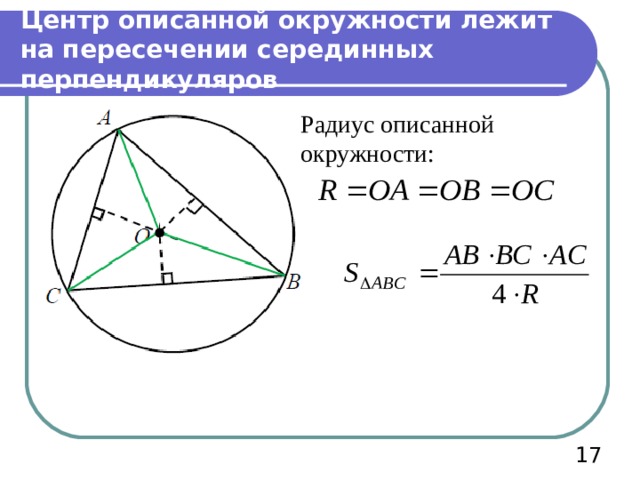
Центр описанной окружности лежит на пересечении серединных перпендикуляров

Радиус описанной окружности:

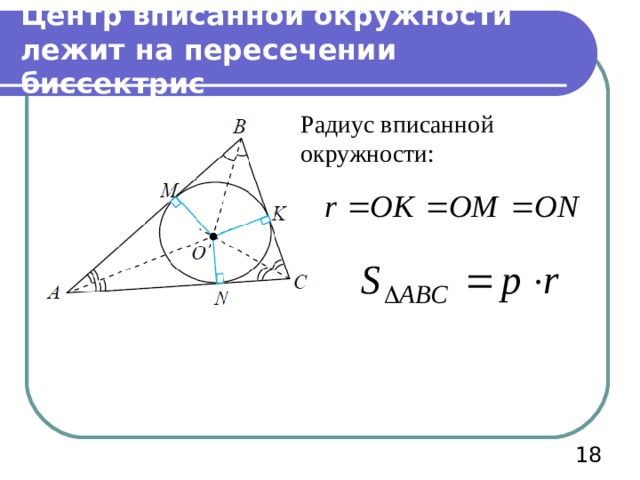
Центр вписанной окружности лежит на пересечении биссектрис

Радиус вписанной окружности:

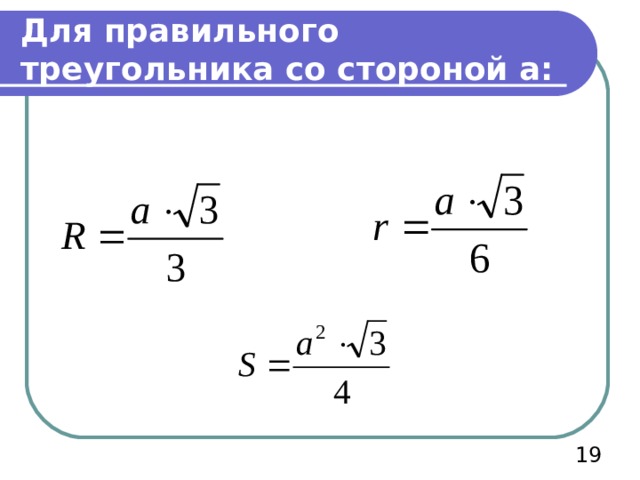
Для правильного треугольника со стороной а:

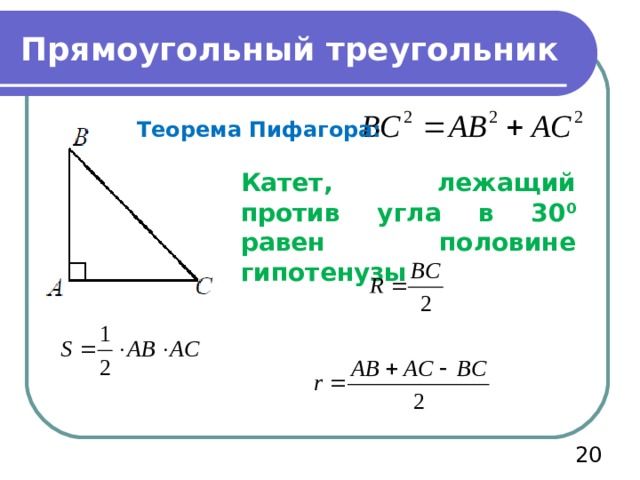
Прямоугольный треугольник

Теорема Пифагора:

Катет, лежащий против угла в 30 0 равен половине гипотенузы

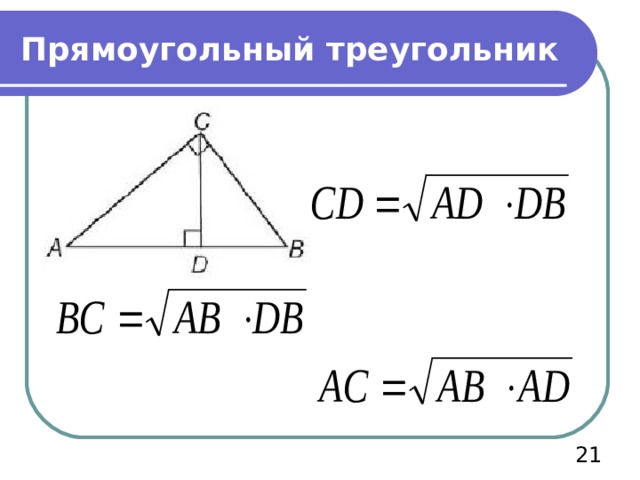
Прямоугольный треугольник

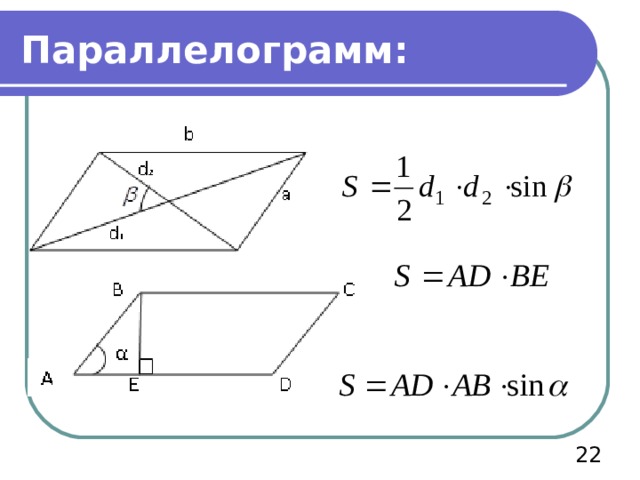
Параллелограмм:

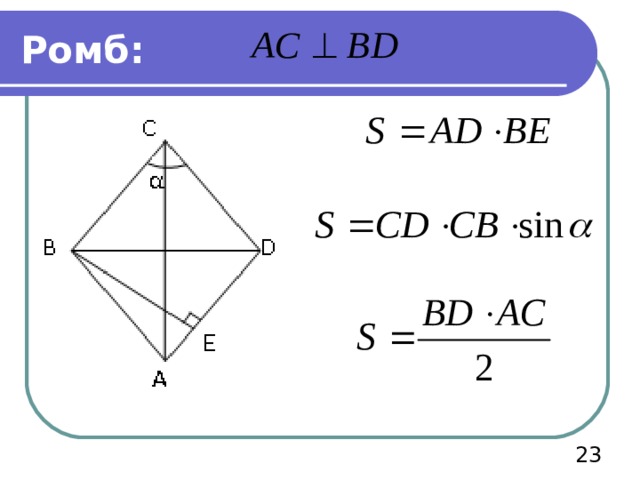
Ромб:

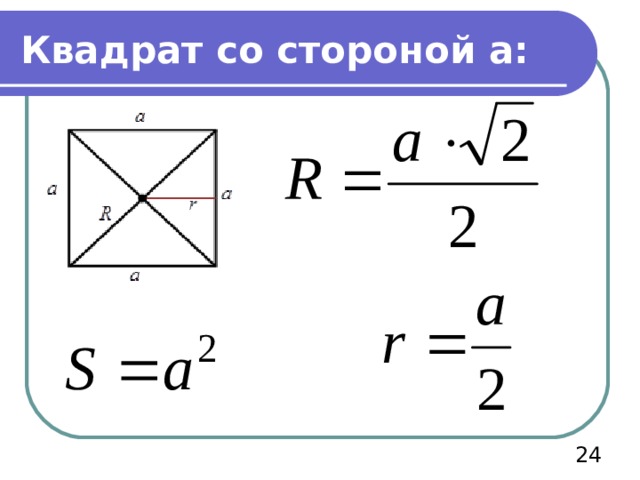
Квадрат со стороной а:

Пример 1

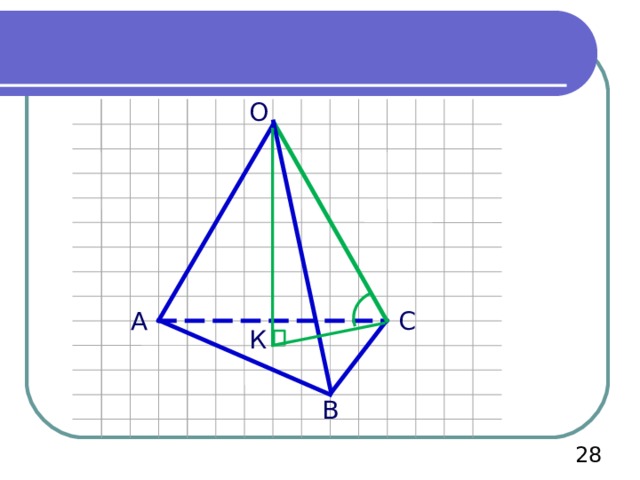
Решение. Первым шагом построим данный многогранник:

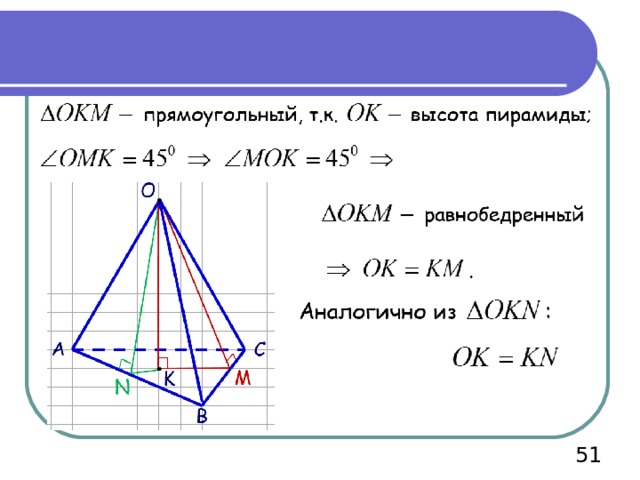
Т.к. пирамида – правильная, то в основании – правильный треугольник, а высота «падает» в центр вписанной и описанной окружности. Все ребра наклонены к основанию под углом 45 0

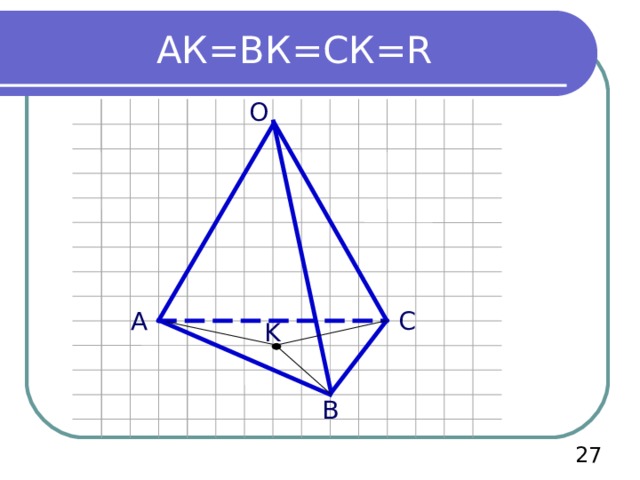
АК=ВК=СК= R

О

А

С

K

В

О

А

С

К

В

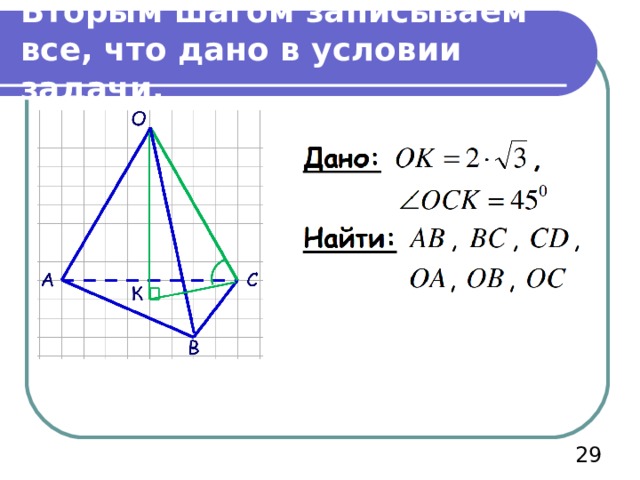
Вторым шагом записываем все, что дано в условии задачи.

28

Т.к. пирамида – правильная, то

СА

Ответ: боковые ребра пирамиды-

Сторона основания пирамиды-

a = 6

Пример 2

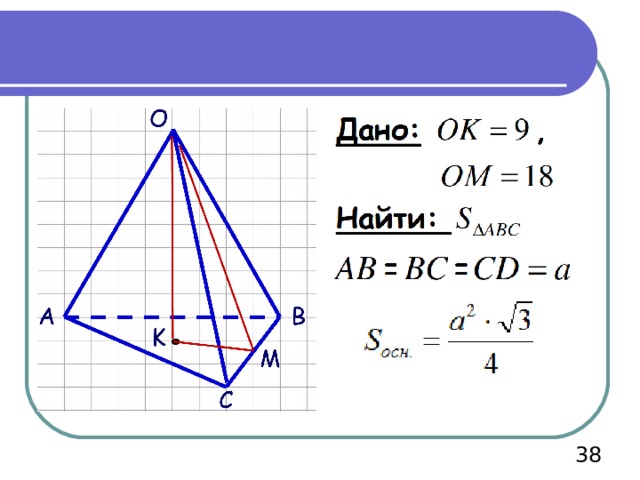
Найти площадь основания правильной треугольной пирамиды, если ее высота равна 9, а апофема – 18.

Решение.

Т.к. пирамида – правильная, то в основании – правильный треугольник, а высота «падает» в центр вписанной и описанной окружности.

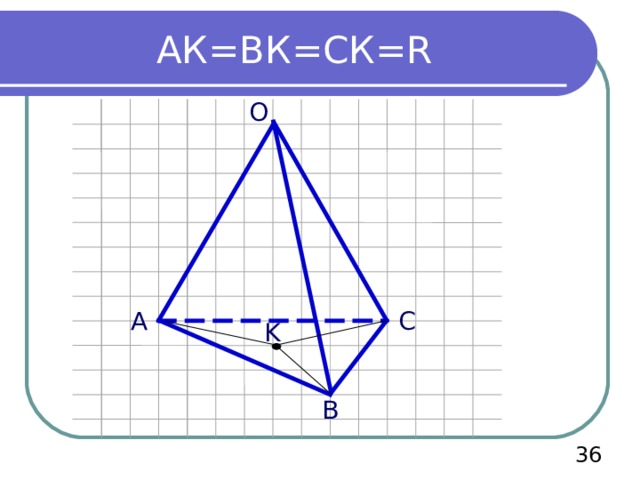
АК=ВК=СК= R

О

А

С

K

В

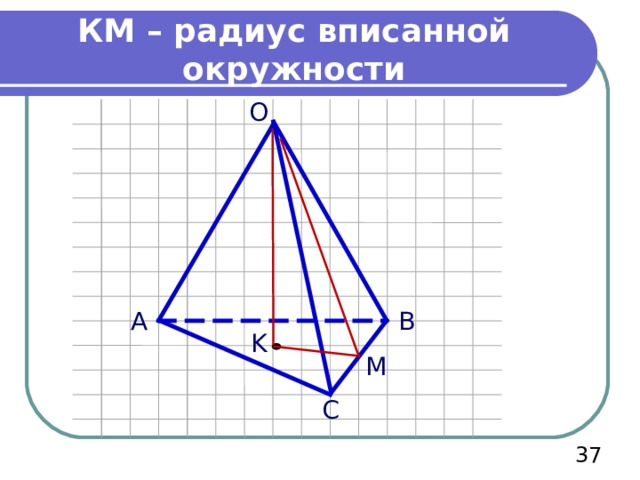
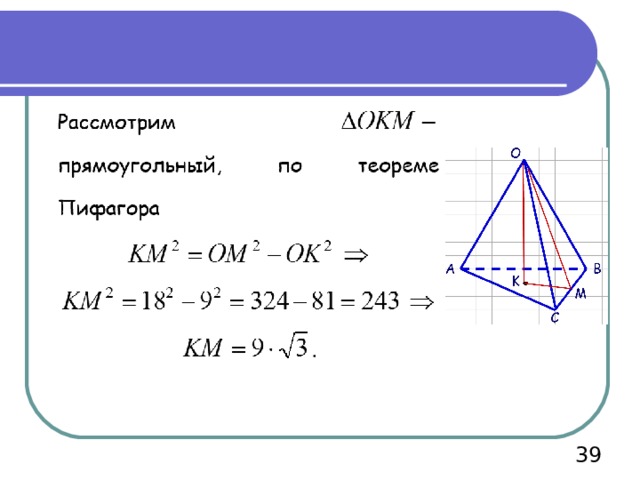
КМ – радиус вписанной окружности

О

В

А

K

М

С

Пример 3

Решение.

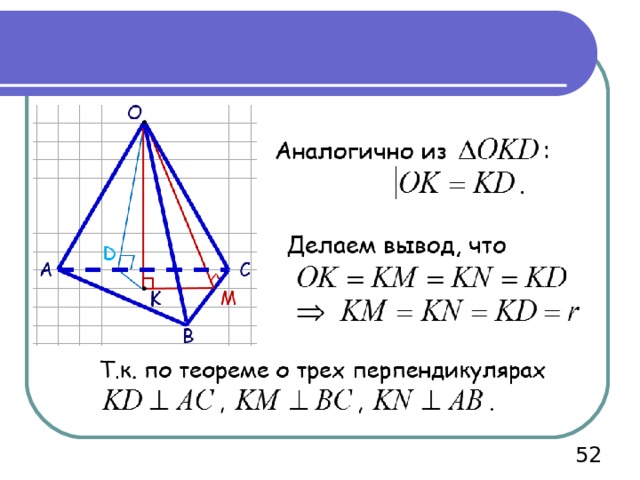
Т.к. пирамида – правильная, то в основании – правильный четырехугольник – квадрат со стороной а, высота «падает» в центр вписанной и описанной окружности.

2

1

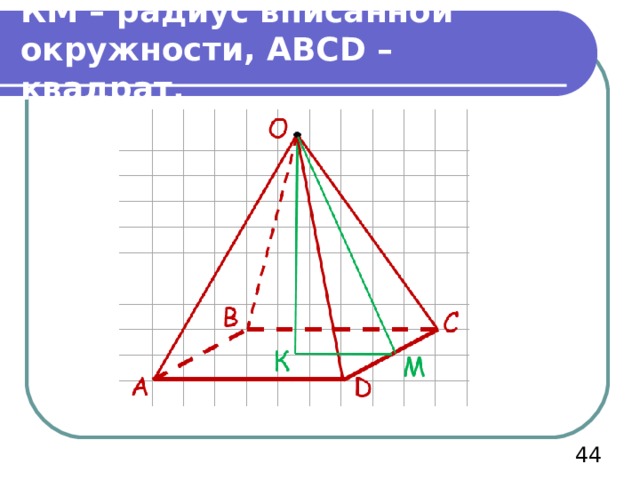
КМ – радиус вписанной окружности, АВС D – квадрат.

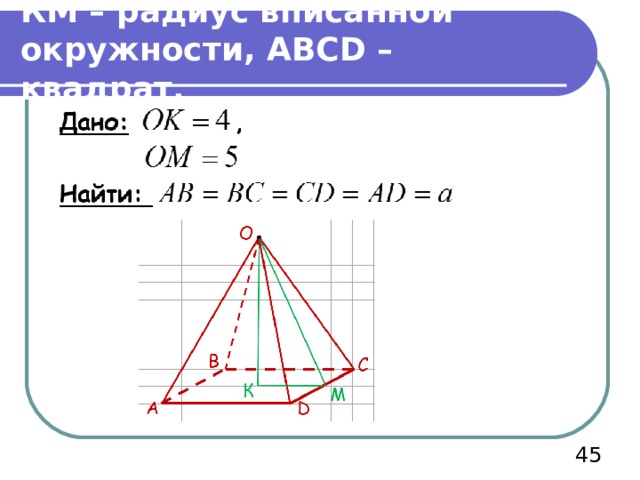
КМ – радиус вписанной окружности, АВС D – квадрат.

Ответ:

Пример 4

Решение.

О

С

А

K

В

О

С

А

М

K

N

В

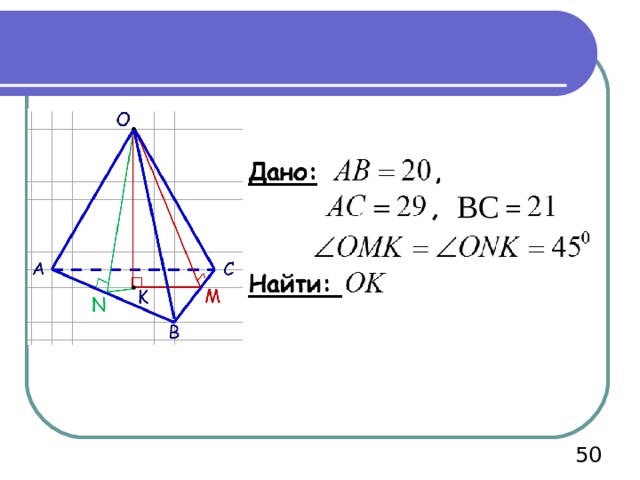
ВС

По формулам:

Следовательно

Тогда:

Ответ: высота пирамиды равна шести.

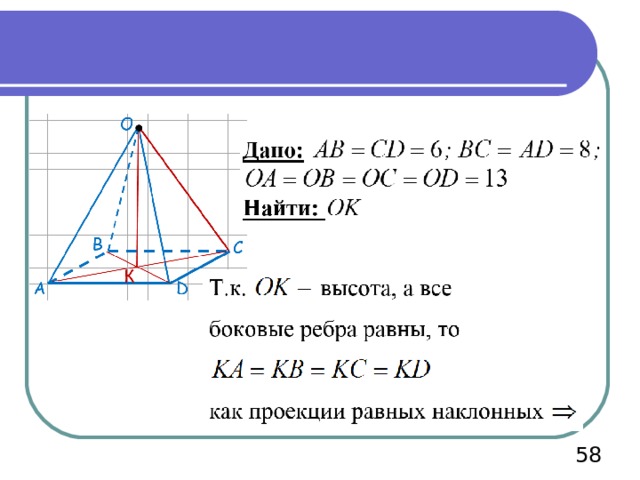
Пример 5

Основание пирамиды – прямоугольник со сторонами 6см. и 8см. Каждое боковое ребро пирамиды равно 13см. Вычислите высоту пирамиды

2

1

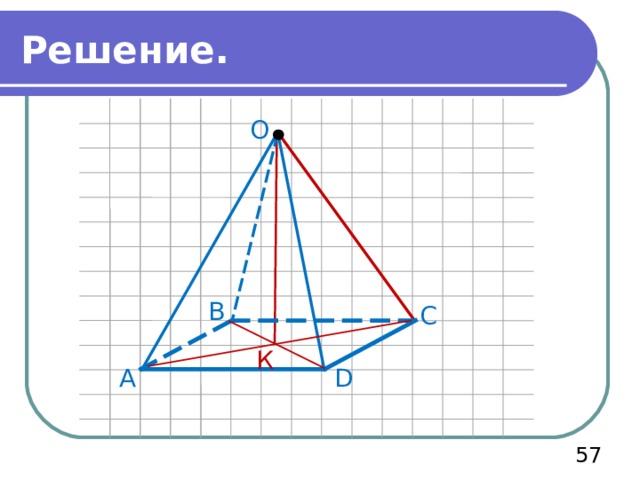
Решение.

О

В

С

К

А

D

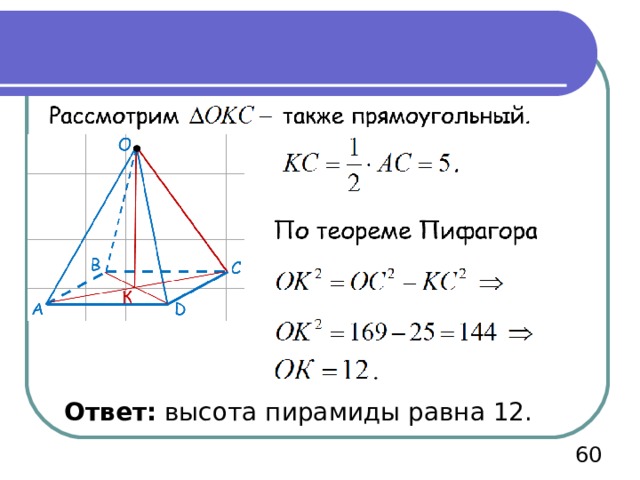
Ответ: высота пирамиды равна 12.

ПЛОЩАДИ ПОВЕРХНОСТЕЙ ПИРАМИДЫ

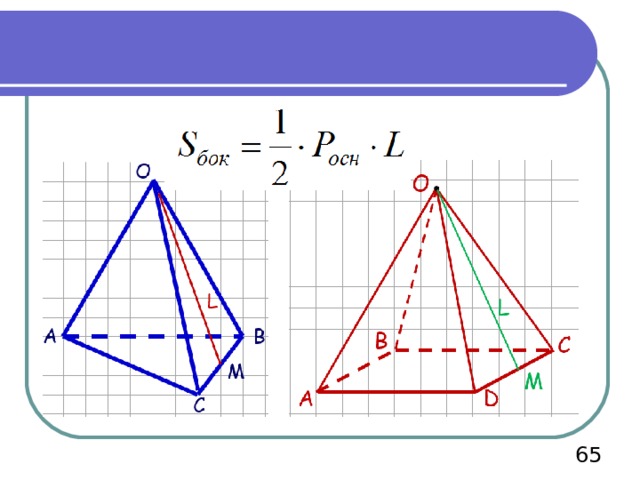
Площадью боковой поверхности пирамиды называется сумма площадей всех ее боковых граней.

Площадь полной поверхности пирамиды — сумма площадей ВСЕХ ее граней, т.е.

Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды.

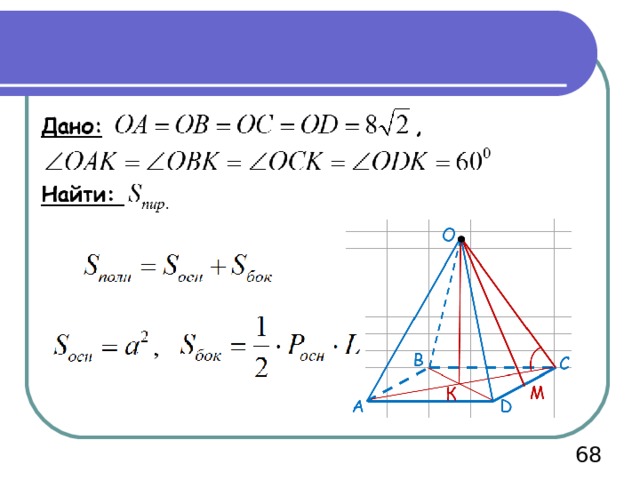
Пример 6

66

Решение.

О

В

С

М

К

А

D

6 8

6 9

Тогда

70

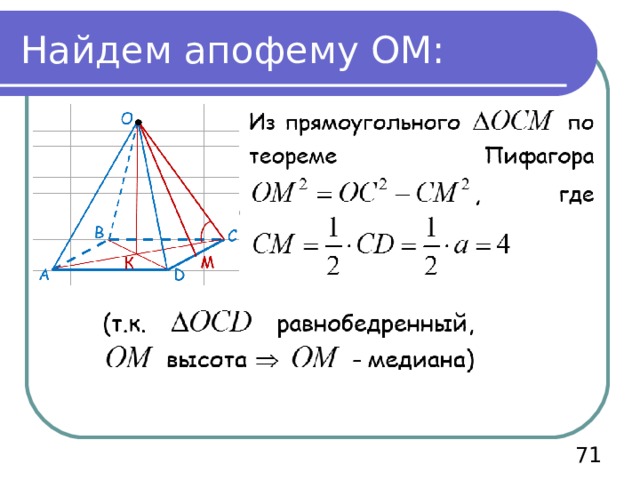
Найдем апофему ОМ:

71

Ответ: площадь поверхности пирамиды равна .

72

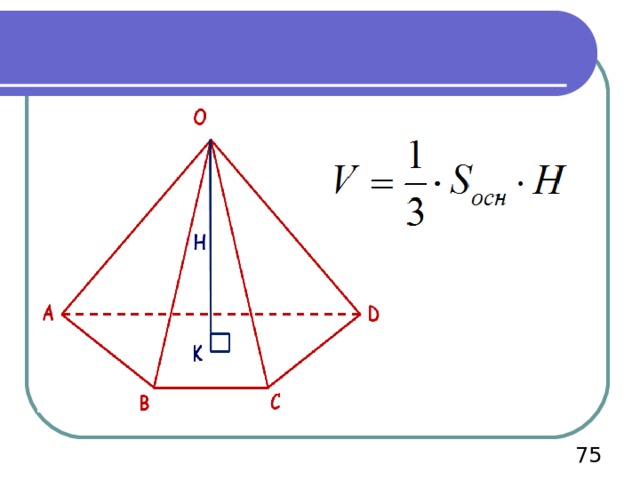
Объем пирамиды

Теорема. Объем пирамиды равен одной трети произведения площади ее основания на высоту.

Пример 7

О

В

А

М

K

С

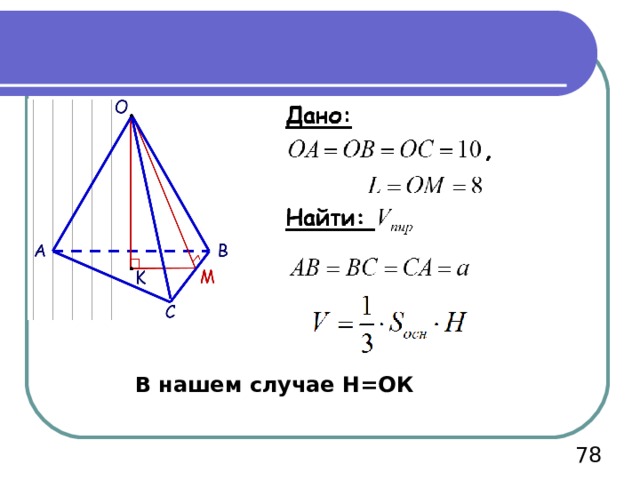
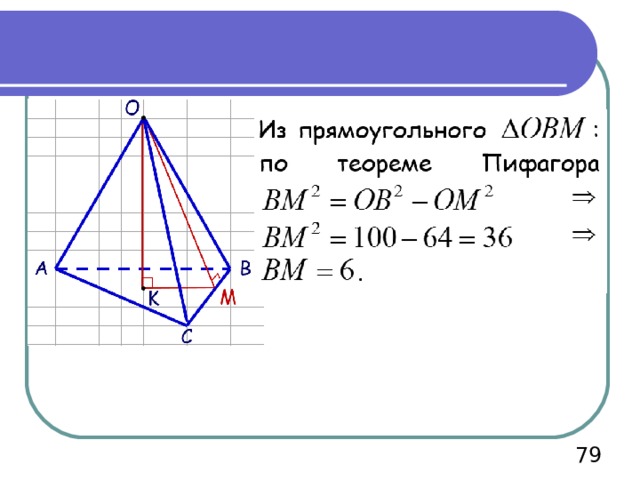
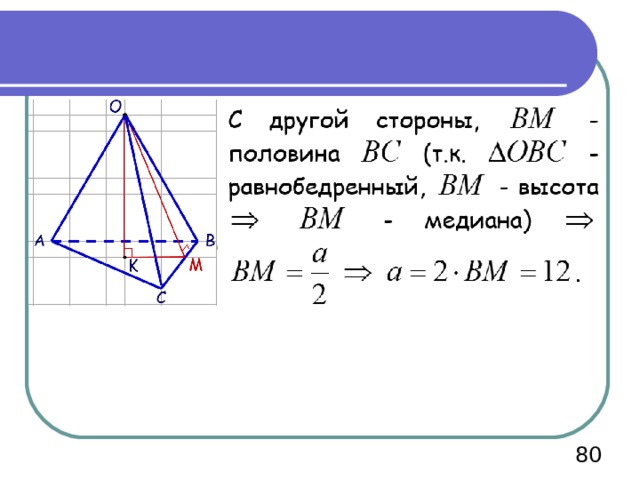
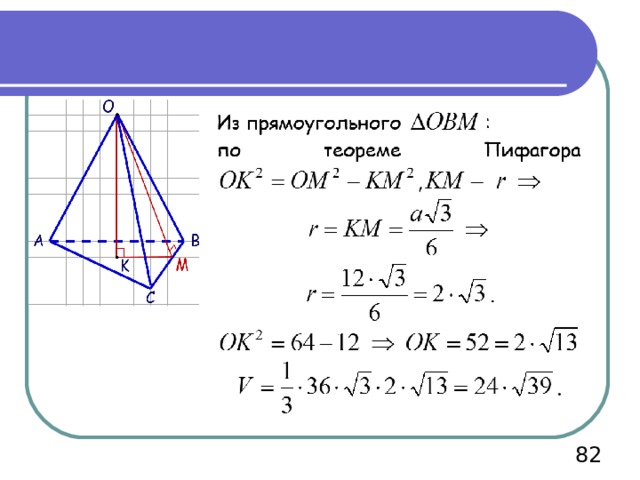
В нашем случае Н=ОК