Пирамида

Презентация содержит 25 слайдов.

Пирамида – многогранник, составленный из n - угольника А1 А2…Аn и n треугольников.

Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины. 

Все апофемы правильной пирамиды равны друг другу.

Злыгостева

Яна Яковлевна

Пирамида Микерина

Пирамида Хефрена

Пирамида Хеопса

Определение

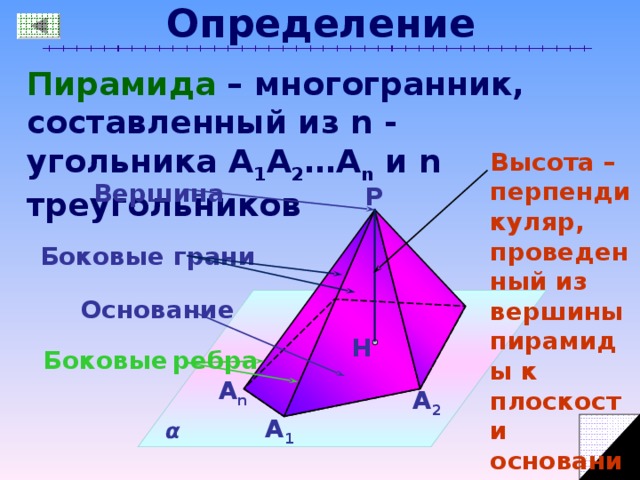
Пирамида – многогранник, составленный из n - угольника А 1 А 2 …А n и n треугольников

Высота – перпендикуляр, проведенный из вершины пирамиды к плоскости основания

Вершина

P

Боковые грани

Основание

H

Боковые ребра

А n

А 2

А 1

α

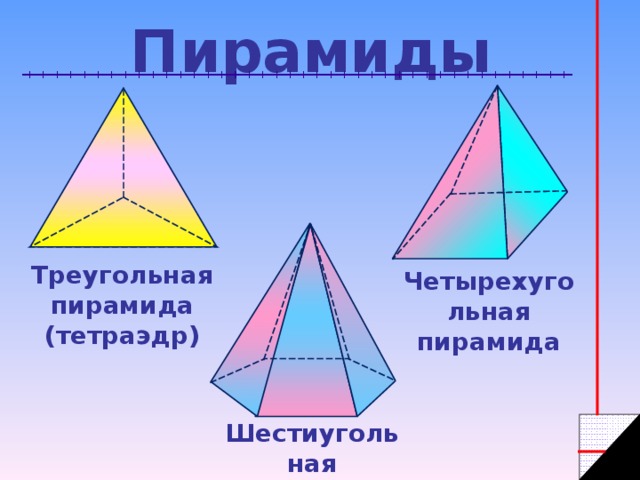
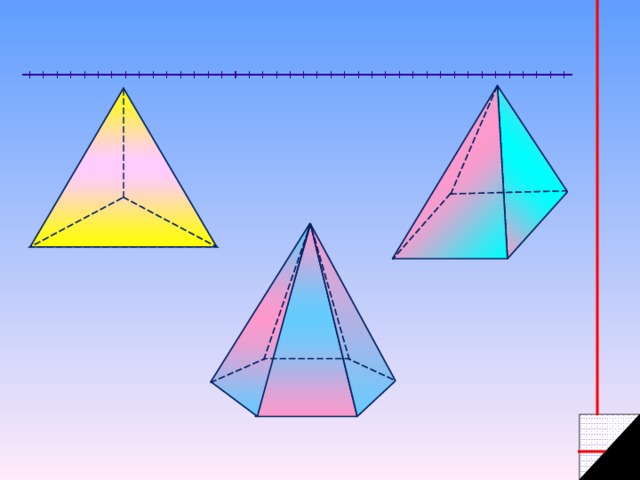
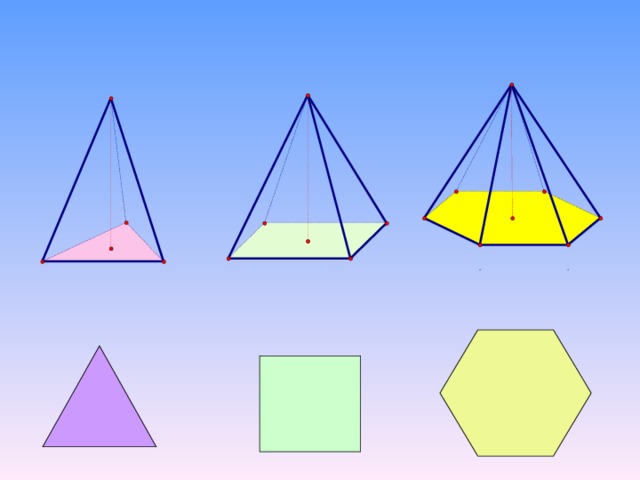
Пирамиды

Треугольная пирамида (тетраэдр)

Четырехугольная пирамида

Шестиугольная пирамида

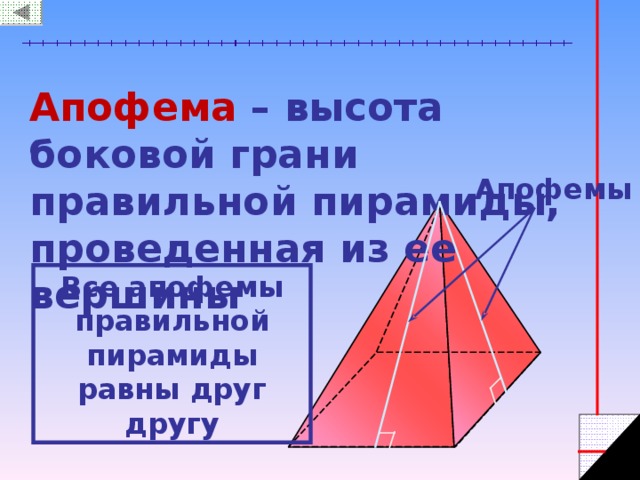
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины

Апофемы

Все апофемы правильной пирамиды равны друг другу

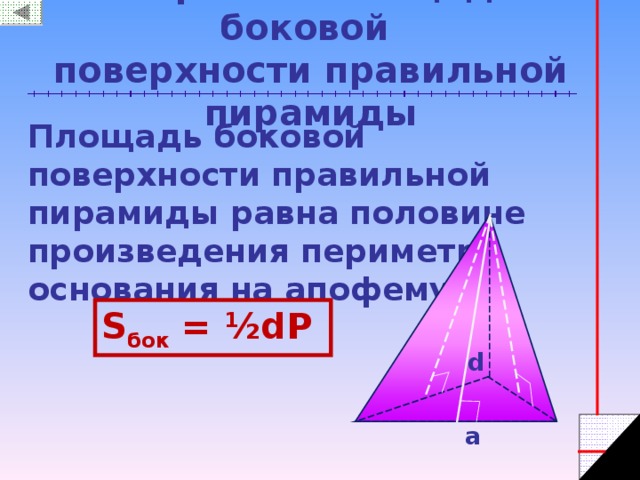
Теорема о площади боковой поверхности правильной пирамиды

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему

S бок = ½dP

d

a

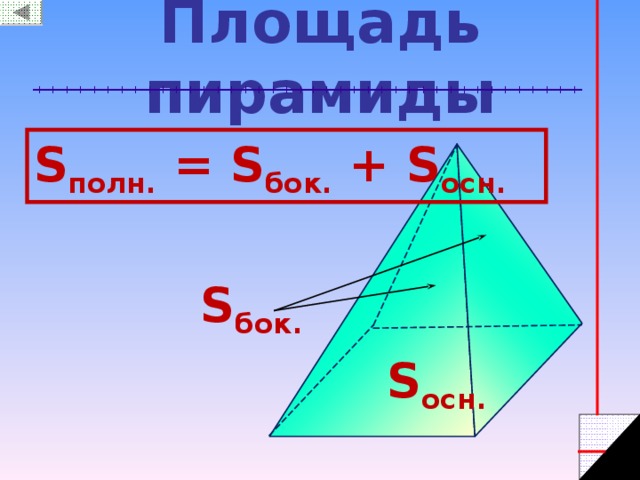
Площадь пирамиды

S полн. = S бок. + S осн.

S бок.

S осн.

V = 1/3 H S осн.

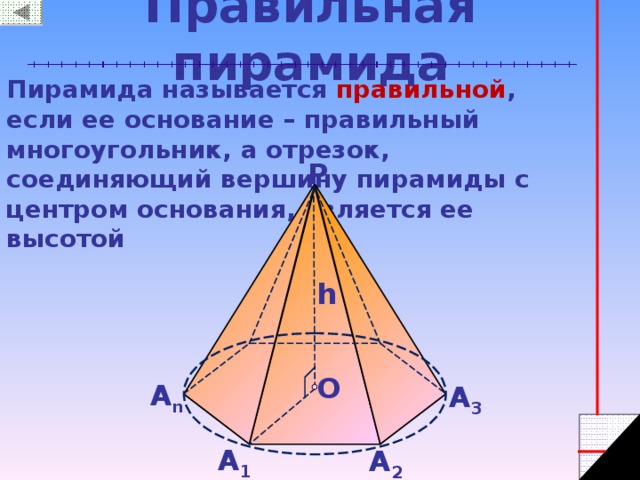
Правильная пирамида

Пирамида называется правильной , если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой

P

h

O

А n

А 3

А 1

А 2

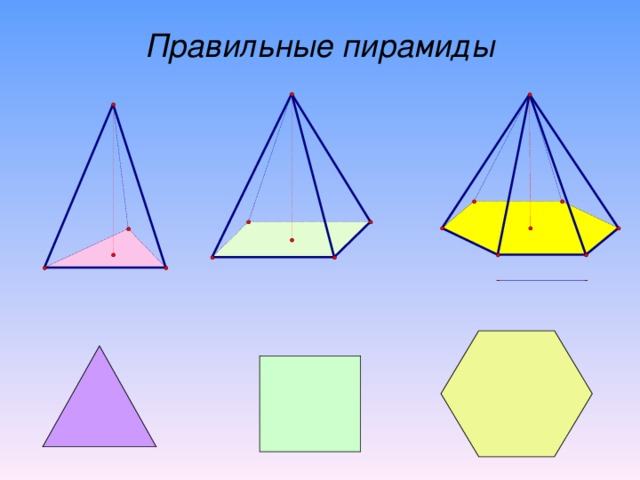
Правильные пирамиды

«Геометрическая задача»

Электрикам требуется провести электропроводку в здании пирамидальной формы.

В основании пирамиды лежит квадрат со стороной 3 0 м , высота пирамиды 8 м . Найти объём этого здания.