Цель урока:
Обеспечить системное повторение, обобщение и закрепление знаний и умений учащихся по теме: «Перпендикулярность в пространстве»
Задачи урока:
Формировать интерес к исследовательской и самостоятельной учебно-познавательной деятельности;
Осуществить контроль и диагностику знаний учащихся по теме;
Развивать умения, навыки умственной работы, творческого мышления, умения использовать теоретические знания при решении практических задач;
Воспитание ответственности и самостоятельности.
Подготовка к семинару:
1. Раздать учащимся заранее вопросы.
2. Девяти учащимся раздать опорные задачи, по которым они готовят сообщения.
3. Двум ученикам подготовит историческую справку по теме семинара.
4. Двум ученикам подготовит вопрос о применении перпендикулярности в науке и жизни.
Вопросы к семинару:
1. Какие прямые в пространстве называются перпендикулярными?
2. Определение перпендикулярности прямой и плоскости.
3. Признак перпендикулярности прямой и плоскости(доказательство на модели).
4. Сколько можно провести в пространстве прямых, перпендикулярных данной прямой через точку, лежащую на прямой и через точку, не лежащую на данной прямой?
5. Что можно сказать о плоскости, перпендикулярной к одной из двух параллельных прямых?
6. как расположены в пространстве 2 прямые перпендикулярные одной и той же плоскости; одной и той же прямой?
7.Определение расстояния от точки до плоскости.
8. Теорема о 3-х перпендикулярах (доказательство по готовым чертежам).
9. Назвать виды параллелограммов, для которых существует точка в пространстве, равноудалённая от всех его вершин .
10. Назвать виды параллелограммов, для которых существует точка пространства, равноудалённая от всех его сторон.
11.Какой должна быть трапеция, чтобы существовала точка пространства, равноудаленная от всех её вершин?
12. В какую точку проектируется точка пространства, равноудалённая от всех вершин треугольника?
13. Как найти радиус окружности, описанной около треугольника, если известны стороны треугольника?
14. В какую точку проектируется точка пространства, равноудалённая от всех сторон треугольника?
15. Как найти радиус окружности, вписанной в треугольник, стороны которого известны?
16. Определение перпендикулярных плоскостей.
17. Признак перпендикулярности плоскостей.
18. Теорема о перпендикулярных плоскостях.
19. Сколько можно провести плоскостей, перпендикулярных данным через точку пространства?
20. Определение общего перпендикуляра двух скрещивающихся прямых.
21. Сколько можно провести общих перпендикуляров к двум скрещивающимся прямым?
22. Определение расстояния между скрещивающимися прямыми?
23. Как практически можно найти расстояние между скрещивающимися прямыми?
Опорные задачи:
Найти проекцию точки пространства, которая равноудалена от всех вершин
n-угольника.
Найти проекцию точки пространства, которая равноудалена от всех сторон
n-угольника.
ABCD- прямоугольник. ВМ АВС. Показать расстояние от точки М до сторон прямоугольника.
Дан неразвёрнутый угол. Точка М равноудалена от сторон угла. Доказать, что проекция точки М лежит на биссектрисе угла.
Через одну из вершин треугольника проведена пря мая, перпендикулярная к его плоскости. Найти расстояние от точки, лежащей на этом перпендикуляре до противолежащей стороны. Рассмотреть случаи: а) треугольник – прямоугольный; перпендикуляр проведён из вершины острого угла; б) треугольник – разносторонний.
Из точек А и В, лежащих в двух перпендикулярных плоскостях опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найти длину отрезка АВ, если АС=α, ВD=b, СD=с.
Перпендикулярные плоскости α и β пересекаются по прямой с. В плоскости α проведена прямая в плоскости β проведена прямая b c. Найти расстояние между прямыми и b, если расстояние между прямыми и с равно m, а между b и с равно n.
Через вершину С треугольника АВС проведена прямая m, перпендикулярная плоскости треугольника. Найти расстояние между прямыми m и АВ.
Через сторону АВ параллелограмма АВСD проведена плоскость α, перпендикулярная плоскости параллелограмма. Найти расстояние между прямой СD и скрещивающейся с ней прямой, лежащей в плоскости α.
Ход семинара:
Учащиеся отвечают на 8 первых вопроса теории.
Учащиеся слушают решение опорных задач 1 и 2.
Учащиеся отвечают на вопросы 9-15.
Дифференцируемая самостоятельная работа ( учащиеся сами выбирают одну задачу из 3-х):
Стороны треугольника равны 14см, 30см, 40см. На каком расстоянии от плоскости треугольника находится точка, удалённая от каждой вершины на 65см?
Стороны треугольника равны 13см, 14см, 15см. На каком расстоянии от плоскости треугольника находится точка, удалённая от всех сторон на 5см?
Катеты прямоугольного треугольника равны 6см, 8см. На каком расстоянии от плоскости треугольника находится точка, удалённая от всех вершин на 13см?
5. Учащиеся слушают решение опорных задач 3, 4, 5.
6. Обсуждение вопросов 16-19.
7. Учащиеся слушают решение опорных задач 6 и 7.
8. Самостоятельная работа. Задача: Концы отрезка АВ=13см лежат на двух взаимно перпендикулярных плоскостях. Из точек А и В опущены перпендикуляры АС и ВD на линию их пересечения. Найти СD, если АС=3см, BD=4см.
9. Учащиеся отвечают на вопросы 20-23.
10. Учащиеся слушают решение опорных задач 8 и 9.
11. Математический диктант по готовому чертежу. Ребро куба равно α.
Найти расстояние между прямыми:
АD и СС1 ;
ВD и АА1;
АС и В1D1;
СС1 и В1D.
12. Историческая справка.
13. Применение перпендикулярности прямых и плоскостей в науке и жизни.
14. Подведение итогов.

 Получите свидетельство
Получите свидетельство Вход
Вход


 АВС. Показать расстояние от точки М до сторон прямоугольника.
АВС. Показать расстояние от точки М до сторон прямоугольника.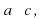 в плоскости β проведена прямая b
в плоскости β проведена прямая b c. Найти расстояние между прямыми
c. Найти расстояние между прямыми 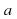 и b, если расстояние между прямыми
и b, если расстояние между прямыми 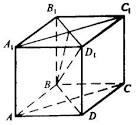 Найти расстояние между прямыми:
Найти расстояние между прямыми:








 Перпендикулярность в пространстве (математика) (20.96 КB)
Перпендикулярность в пространстве (математика) (20.96 КB)
 0
0 1083
1083 121
121 Нравится
0
Нравится
0



