Объем прямоугольного параллелепипеда.
Сегодня мы решим одну задачу и найдем объем прямоугольного параллелепипеда. Для начала посмотрим, что это за математический зверь такой - прямоугольный параллелепипед. Вот как он выглядит.
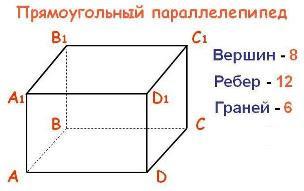
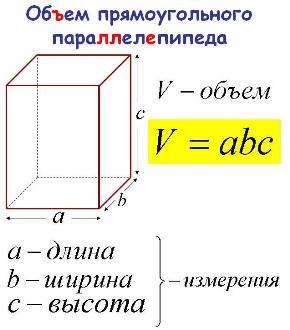
Как видите, прямоугольный параллелепипед скорее похож на клетку для зверей, чем на самого зверя. Математики считают, что живет этот параллелепипед в геометрии, в 5 классе. Они просто забыли, что в детском садике параллелепипед был одной из их игрушек. Детский кубик - это тоже прямоугольный параллелепипед, у которого все грани равной длины. У параллелепипеда есть 8 вершин, 12 ребер и 6 граней.
Это трехмерная (или объемная) фигура. Двухмерные грани, одномерные ребра и точки вершин обозначают границы трехмерного пространства, которое заключено внутри параллелепипеда. Прямоугольным эту геометрическую фигуру называют потому, что все углы в нем прямые - равные 90 градусов или пи/2. Внутренне пространство этой клетки называется объемом. Кстати, мы очень любим сажать друг друга в клетки параллелепипедов.
Или прятаться внутри них - комнаты часто имеют форму параллелепипедов. Стены, пол и потолок - так мы называем грани комнаты. Ребра мы называем углами, нижние ребра мы стыдливо прячем за плинтус, верхние ребра или выставляем на показ, или украшаем потолочным багетом. Точки, в которых пересекаются углы комнаты, являются вершинами параллелепипеда, в котором мы живем. Ой, что-то мы сильно отвлеклись на экскурсию по достопримечательностям параллелепипеда, давайте посмотрим, как нужно считать его объем.
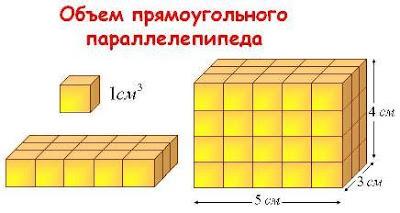
Общий объем параллелепипеда состоит из маленьких кубиков единиц измерения объема, который на рисунке измеряется в кубических сантиметрах. Измерять объем можно и в других единицах измерения - кубических метрах (например, объем комнаты), кубических километрах (когда будем мерить планету), литрах (жидкости, но моря и океаны лучше измерять в кубических километрах). Объемы звездных систем и галактик можно мерить в кубических световых годах.
Интересно, а в чем лучше измерять объемы разных вселенных? Как вы видите, любой трехмерный объем является умножением трех перпендикулярных единиц измерения длины. У прямоугольного параллелепипеда три ребра всегда перпендикулярны в вершинах. Длина таких ребер называется линейными размерами или измерениями прямоугольного параллелепипеда.

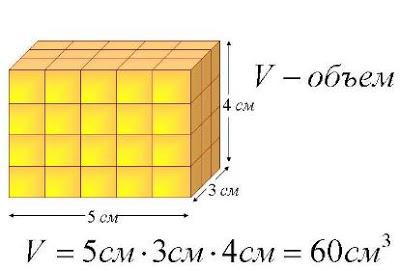
Если избрать единицу измерения и количество этих единиц в каждом из трех измерений, тогда легко можно высчитать объем прямоугольного параллелепипеда по формуле - перемножить все три линейных (перпендикулярных) размера.
Математики никогда не обращают на это особого внимания, но нужно не забывать, что во всех трех направлениях единицы измерения длины должны быть одинаковыми. Если у какой-то штучки один размер значительно больше двух других размеров, то тогда такую штучку мы меряем в погонных метрах.
Например, железнодорожные рельсы лучше измерять в погонных метрах (километрах), а не в единицах измерения объема. С математической точки зрения, один погонный метр - это единица измерения объемных тел, двумя размерами которых можно пренебречь.
Как видно из рисунка, одним и тем же единицам измерения длины мы присваиваем разные названия. Этим мы уточняем пространственную ориентацию нашего параллелепипеда. Длина и ширина располагаются внизу, при этом длина обычно больше ширины. Высоту мы отмеряем вверх. Все эти названия являются относительными. Если поставить наш параллелепипед на другую грань, названия сторон могут поменяться - длина или ширина превратится в высоту. Объем параллелепипеда не зависит от названий его размеров, поскольку при нахождении объема используются все три линейных размера.
Таким образом, объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты (произведению трех линейных размеров). Как бы мы этот параллелепипед не крутили. Числовое выражение объема зависит от тех единиц измерения, в которых мы выражаем размеры этой геометрической фигуры. В полном соответствии с теоремой Пифагора, все единицы измерения размеров должны быть одинаковы. Возможно, это и звучит, как нравоучение несмышлёным детишкам, но математики считают математику абстрактной наукой именно потому, что они не всегда понимают, что именно, когда и как они делают.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


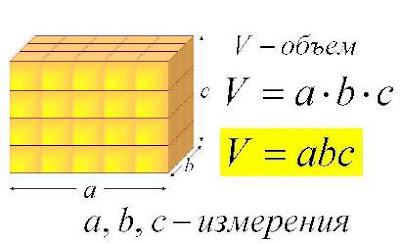











 Материал по математике "Объем прямоугольного параллелепипеда" (0.17 MB)
Материал по математике "Объем прямоугольного параллелепипеда" (0.17 MB)
 0
0 2254
2254 58
58 Нравится
0
Нравится
0









