Перевод десятичных и двоичных дробных чисел

Повторим

1. Переведите число из десятичной системы счисления в восьмеричную и шестнадцатеричную: 218₁₀.

2.  Переведите числа в десятичную систему  счисления: 10111₂, 3AF₁₆.

Вывод алгоритма перевода десятичных дробей в двоичную систему счисления

Разложим  двоичную дробь Адд в ряд по основанию 2

Aдд = а-1*2-1 + a-2*2-2 + ... – получим запись  в развернутой форме двоичной дроби, так как в этой записи будут отсутствовать положительные степени основания, т. е. числа 2

1. Умножим число  Адд на основание двоичной системы, т. е. на 2. Произведение будет равно:  а_-1 + a_-2*2^-1 + ...

Целая часть равна а-1, именно это число и является значением первого дробного разряда двоичного числа.

2. Оставшуюся дробную часть опять умножаем на 2, получим целую часть, равную а0, именно это число и является значением второго дробного разряда двоичного числа.

Описанный процесс  продолжается до получения нулевой дробной части или  до достижения требуемой точности вычислений.

Заметим, что последовательность полученных чисел совпадает с последовательностью цифр дробного двоичного числа, записанного в свернутой форме: Aдд = а-1 a-2 …..

Аналогичные рассуждения могут быть проведены и для перевода дробных десятичных чисел в восьмеричную и шестнадцатеричную системы счисления.

1. Переведите число из десятичной системы

счисления в восьмеричную и шестнадцатеричную: 218 10 .

2.  Переведите числа в десятичную систему

счисления: 101 11 2 , 3AF 16 .

• 1. Переведите число из десятичной системы счисления в восьмеричную и шестнадцатеричную: 218 10 . 2.  Переведите числа в десятичную систему счисления: 101 11 2 , 3AF 16 .

Разложим двоичную дробь А дд в ряд   по основанию 2

A дд =  а - 1 * 2 -1  + a - 2 * 2 -2  + ... – получим запись в развернутой форме двоичной дроби, так как в этой записи будут отсутствовать положительные степени основания, т. е. числа 2

1. Умножим число  А дд   на основание двоичной системы, т. е. на 2. Произведение будет равно: а - 1  + a - 2 * 2 -1  + ...

Целая часть равна  а - 1 , именно это число и является значением первого дробного разряда двоичного числа.

2. Оставшуюся дробную часть опять умножаем на 2, получим целую часть, равную а 0 , именно это число и является значением второго дробного разряда двоичного числа.

Описанный процесс продолжается до получения нулевой дробной части или до достижения требуемой точности вычислений.

Заметим, что последовательность полученных чисел совпадает с последовательностью цифр дробного двоичного числа, записанного в свернутой форме: A дд =  а - 1 a - 2 …..

Аналогичные рассуждения могут быть проведены и для перевода дробных десятичных чисел в восьмеричную и шестнадцатеричную системы счисления.

• Последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы счисления (на 2, 8 или 16) до тех пор, пока не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений.

2 . Получить искомую двоичную , восьмеричную или шестнадцатеричную дробь, записав полученные целые части произведений в прямой последовательности.

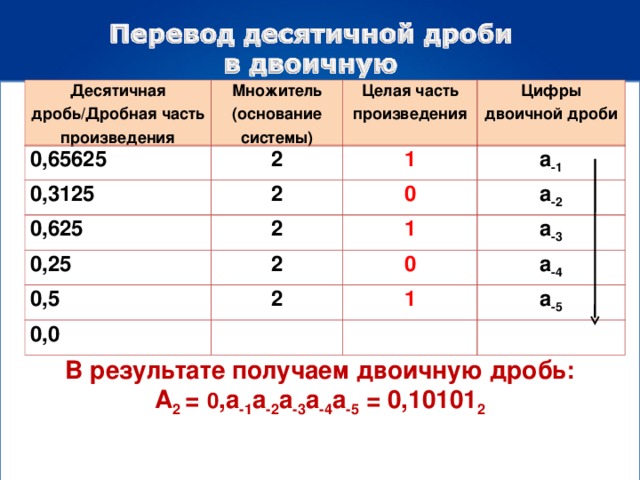
Десятичная дробь/Дробная часть произведения

Множитель (основание системы)

Целая часть произведения

Цифры двоичной дроби

В результате получаем двоичную дробь:

А 2 = 0 ,а -1 а -2 а -3 а -4 а -5 = 0,10101 2

0,65625

2

1

а -1

0,3125

2

0

а -2

0,625

2

1

а -3

0,25

2

0

а -4

0,5

2

1

а -5

0,0

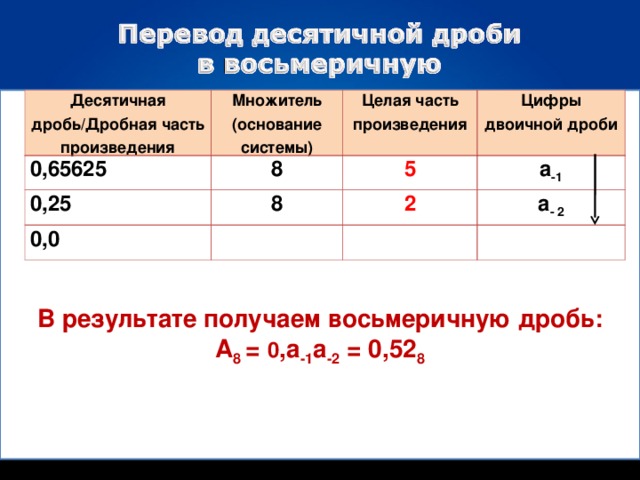
В результате получаем восьмеричную дробь:

А 8 = 0 ,а -1 а -2 = 0,52 8

Десятичная дробь/Дробная часть произведения

Множитель (основание системы)

Целая часть произведения

Цифры двоичной дроби

0,65625

8

5

а -1

0,25

8

2

а - 2

0,0

В результате получаем

шестнадцатеричную дробь:

А 16 = 0 ,а -1 а -2 = 0,А8 16

Десятичная дробь/Дробная часть произведения

Множитель (основание системы)

Целая часть произведения

Цифры двоичной дроби

0,65625

16

10(А)

а -1

0,5

16

8

а - 2

0,0

Перевод производится в два этапа:

• целая часть числа находится делением на основание новой системы счисления;
• дробная часть числа находится умножением на основание новой системы счисления.

В итоговой записи полученного числа целая часть от

дробной отделяется запятой.

Переведем 35,25 10  в восьмеричную систему :   Целая часть числа находится делением на основание новой системы

35

-32

8

4

3

Дробная часть числа находится умножением на основание новой системы

0

,

2

,25

8

0

Получилось: 35 10  = 43 8  

Получилось: 0,25 10  = 0,2 8  

Сложим вместе целую и дробную части:

43 8  + 0,2 8  = 43,2 8   Результат перевода :  35,25 10  = 43,2 8

Число необходимо представить в разложении по

степеням той системы счисления, в которой находится

число.

Пример 1:  0,110 2  = 0∙2 0  + 1∙2 -1  + 1∙2 -2  + 0∙2 -3  = 0,75 10

Пример 2: 0,5 8  = 0∙8 0  + 5∙8 -1  = 0,625 10

Пример 3: 0,8 16  = 0∙16 0  + 8∙16 -1  = 0,5 10  

Заполните таблицу, в каждой строке которой одно и то же дробное число должно быть записано в различных системах счисления .

Двоичная

Восьмерич-ная

0,101

Десятичная

0,6

Шестнадца-теричная

0,125

0,4

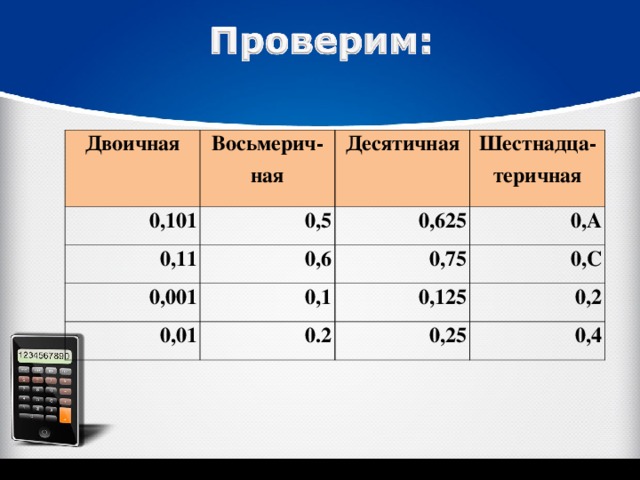
Двоичная

Восьмерич-ная

0,101

0,5

0,11

Десятичная

0,001

0,6

0,625

Шестнадца-теричная

0,А

0,1

0,75

0,01

0,С

0,125

0.2

0,2

0,25

0,4

1 строка

Одно слово - существительное

2 строка

Два слова – прилагательные или причастия (к первой строчке)

3 строка

Три слова – глаголы (к первой строчке)

4 строка

Четыре слова – предложение (фраза, которая показывает отношение к первой строчке)

5 строка

Одно слово – ассоциация, синоним, повторяющий суть первой строчки