Определение. Соответствие между элементами множеств X и Y называется отображением X в Y, если каждому элементу х из множества X соответствует только один элемент множества Y.
Этот элемент называют образом элемента х при данном отображении.
На графе отображения от каждого элемента, принадлежащего множеству X, отходит только одна стрелка.
Если отображение X в Y таково, что каждый элементу из множества Y соответствует одному или нескольким элементам множества X, то такое отображение называют отображением множества X на множество Y.
Другими словами, это означает, что область прибытия отображения совпадает с его множеством значений. На графе такого отображения в множестве Y нет свободных элементов (элементов, не участвующих в отображении).
Отображение множества X на множество Y называется взаимно однозначным, если каждому элементу х из множества X соответствует единственный элементу из множества Y, а каждый элементу из множества Y соответствует только одному элемент)' л* из множества X.
Определение. Два множества X и Y называются равномощными, если существует взаимно однозначное отображение множества X на множество Y. Если X равномощно Y, то пишут: X ~ Y.
Определение. Бесконечное множество X называют счетным, если оно равномощно множеству натуральных чисел, т.е. X ~ |
Пример 1. Между элементами множеств X и Y задано соответствие «быть делителем». Установите, является ли оно отображением X в Y, если: а) X = {2, 3, 5, 7}, Y = {15, 28, 37}; б) X = {2, 3, 5, 7}, Y = {15, 21, 30}.
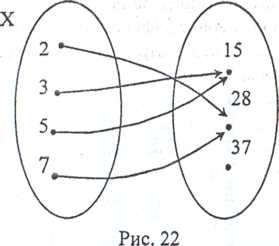
Решение, а) Построим граф данного соответствия (рис. 22). Видим, что каждому элементу множества X соответствует только один элемент из множества Y.
Следовательно, данное соответствие является отображением X в У. Но его нельзя назвать отображением X на Y, поскольку не каждый элемент из множества Y соответствует элементам множества X.
Так, число 37 не соответствует ни одному, элементу из множества X.

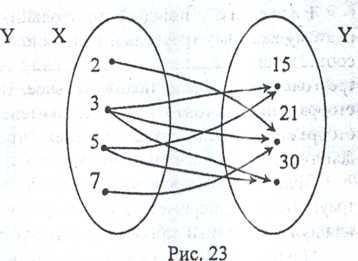
б) Так же, как и в предыдущем случае, построим граф заданного соответствия (рис. 23). Видим, что некоторым элементам из множества X соответствует более одного элемента множества Y (например, числу 3 соответствуют числа 15, 21 и 30). Поэтому соответствие «быть делителем» между элементами множеств X и Y не является отображением X в Y.
Пример 2. На рис. 24 приведены графы отображений множества А на множество В. Выясните, какой из них задает взаимно однозначное отображение множества А на множество В.
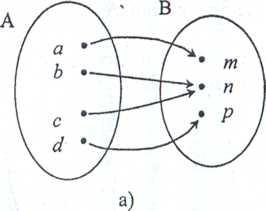
Решение. Отображение, граф которого изображен на рис. 24 а), не является взаимно однозначным отображением А на В, так как не каждый элемент из множества В соответствует единственному элементу из множества А. Например, элемент п соответствует элементам Ъ и с.
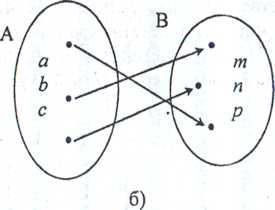
Отображение, граф которого изображен на рис. 24 б) таково, что каждый элемент из множества В соответствует только одному элементу
множества А. Следовательно, имеем взаимно однозначное отображение множества А на множество В.
Пример 3. Пусть X - множество всех треугольников плоскости, У = R - множество всех действительных чисел. Выберем, единицу измерения длин и сопоставим каждому треугольнику число - периметр этого треугольника. Будет ли это соответствие отображением? Каким? Каков полный прообраз числа у е R1
Решение. Каждый треугольник имеет определенный периметр, поэтому каждому треугольнику из множества X сопоставляется при данном соответствии единственное число - его периметр.
Но периметр треугольника - число положительное, поэтому множество значений этого отображения состоит из всех положительных действительных чисел.
Имеем отображение множества X всех треугольников в множество всех действительных чисел и на множество всех положительных чисел.
Если у - положительное число, то полный прообраз у состоит из всех треугольников, периметр которых равен у. Если у - отрицательное число или нуль, то полный прообразу есть пустое множество.
Пример 4. Докажите, что счетным является: а) множество нечетных натуральных чисел; б) множество целых чисел, делящихся на 3.
Решение, а) Счетным является множество, равномощное множеству натуральных чисел. Следовательно, нужно установить взаимно однозначное отображение множества нечетных натуральных чисел на множество 7V.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Отображения (49.71 КB)
Отображения (49.71 КB)
 0
0 1586
1586 60
60 Нравится
0
Нравится
0





