Основы логики
- Логические выражения и операции
- Таблицы истинности
- Логические элементы компьютера
- Логические задачи
Тема 1. Логические выражения и операции
Булева алгебра
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля . Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логические высказывания
Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно.
Высказывание или нет ?
- Организм человека на 65% состоит из воды. 6 – четное число. История – интересный предмет. У квадрата – 10 сторон и все разные. Красиво! Сектор – часть круга. Который час? Ученик 10 класса. Х больше 20.
- Организм человека на 65% состоит из воды.
- 6 – четное число.
- История – интересный предмет.
- У квадрата – 10 сторон и все разные.
- Красиво!
- Сектор – часть круга.
- Который час?
- Ученик 10 класса.
- Х больше 20.
Логические высказывания
Предложения типа:
" В городе A более миллиона жителей ",
" У него голубые глаза "
?
?
!
Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
" В городе N живут 2 миллиона человек."
5
Логические высказывания
- зачастую трудно установить истинность высказывания
Например:
" Площадь поверхности Индийского океана
равна 75 млн кв. км "
" В романе «Война и мир» 431235 слов "
1
0
5
Логические переменные
Логическая переменная – это простое высказывание, содержащее только одну мысль .
Ее символическое обозначение – латинская буква (например, A , B , X , Y и т.д.).
А - «Число 12 - четное».
В - «2*2=5».
А = 1
В = 0
!
Любое высказывание может быть ложно (0) или истинно (1).
Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0).
7
5 . Число 5 отрицательное или нечетное. Сейчас идет урок логики. 3 – четное число. Буква «а» - гласная. Кто отсутствует? Париж – столица Англии. Число 11 является простым. Сложите числа 2 и 5. 2*2=4 и 4 5 . Число 5 отрицательное или нечетное. А = 1 B = 0 C = 1 D = 0 X = 1 Y = ? Y = ? 7 " width="640"
7
Логические переменные
Какие из предложений являются высказываниями?
Определите истинность простых высказываний .
- Сейчас идет урок логики. 3 – четное число. Буква «а» - гласная. Кто отсутствует? Париж – столица Англии. Число 11 является простым. Сложите числа 2 и 5. 2*2=4 и 4 5 . Число 5 отрицательное или нечетное.
- Сейчас идет урок логики.
- 3 – четное число.
- Буква «а» - гласная.
- Кто отсутствует?
- Париж – столица Англии.
- Число 11 является простым.
- Сложите числа 2 и 5.
- 2*2=4 и 4 5 .
- Число 5 отрицательное или нечетное.
А = 1
B = 0
C = 1
D = 0
X = 1
Y = ?
Y = ?
7
Логические связки
7
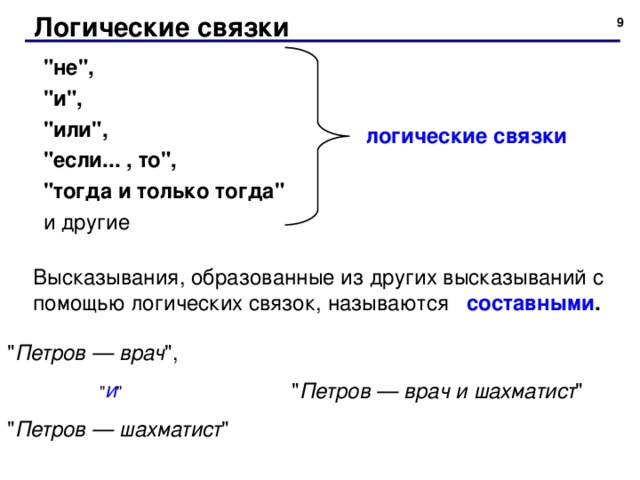
"не",
"и",
"или",
"если... , то",
"тогда и только тогда"
и другие
логические связки
Высказывания, образованные из других высказываний с помощью логических связок, называются составными .
" Петров — врач ",
" Петров — шахматист "
" и "
" Петров — врач и шахматист "
Логические связки
7
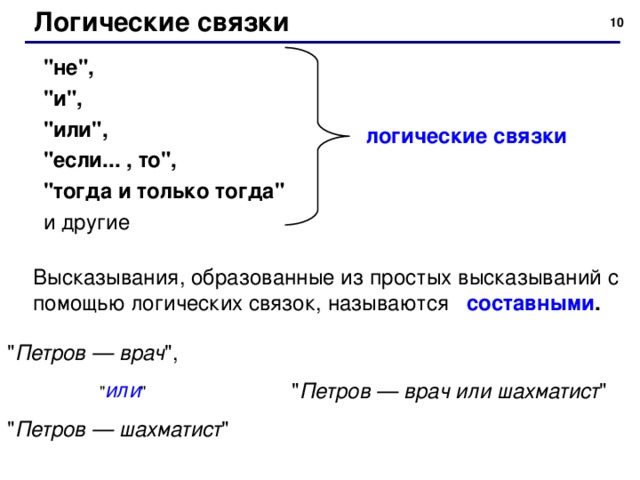
"не",
"и",
"или",
"если... , то",
"тогда и только тогда"
и другие
логические связки
Высказывания, образованные из простых высказываний с помощью логических связок, называются составными .
" Петров — врач ",
" Петров — шахматист "
" или "
" Петров — врач или шахматист "
7
Обозначение высказываний
A – Сейчас идет дождь.
B – Форточка открыта.
простые высказывания (элементарные)
Составные высказывания строятся из простых с помощью логических связок ( операций ) " и ", " или ", " не ", " если … то ", " тогда и только тогда " и др.
A и B
A или не B
если A , то B
не A и B
A тогда и только
тогда, когда B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
Если сейчас идет дождь, то форточка открыта.
Сейчас нет дождя и форточка открыта.
Дождь идет тогда и только тогда, когда открыта форточка.
7
7
Обозначение высказываний
A – Тимур поедет летом на море.
B – Тимур летом отправится в горы.
простые высказывания
Постройте сложные высказывания с помощью логических связок:
A и B
A или не B
если A , то B
не A и B
A тогда и только
тогда, когда B
Тимур поедет летом на море и отправится в горы.
Тимур поедет летом на море или не отправится в горы.
Если Тимур поедет летом на море, то он также отправится в горы.
Тимур поедет летом не на море, а отправится в горы.
Тимур летом поедет на море тогда и только тогда, когда побывает в горах.
7
7
7
1.Операция ОТРИЦАНИЕ (инверсия)
инверсия – от лат. inversion - переворачиваю
В естественном языке ей соответствует выражение " неверно, что… ", относящееся ко всему высказыванию, или присоединение союза " не " к некоторой части простого высказывания.
Обозначение: Ā , А
А – "Сейчас идет дождь",
отрицание А – "Неверно, что сейчас идет дождь",
или " Сейчас дождь не идет", или "Дождь идет не сейчас".
В – "Утки зимуют на юге",
С - "Снег выпал летом ",
D - "Луна – спутник Земли"
7
7
Операция ОТРИЦАНИЕ ( инверсия)
А - «Число 12 - четное».
А = 1
" не А " - «Число 12 - нечетное».
Ā = 0
В - «2*2=5».
В = 0
" не В " - «2*2 ≠ 5».
не В = 1
Таблица истинности логического выражения Х – это таблица, определяющая значение сложного высказывания при всех возможных значениях простых высказываний.
!
Любое высказывание может быть ложно (0) или истинно (1).
15
15
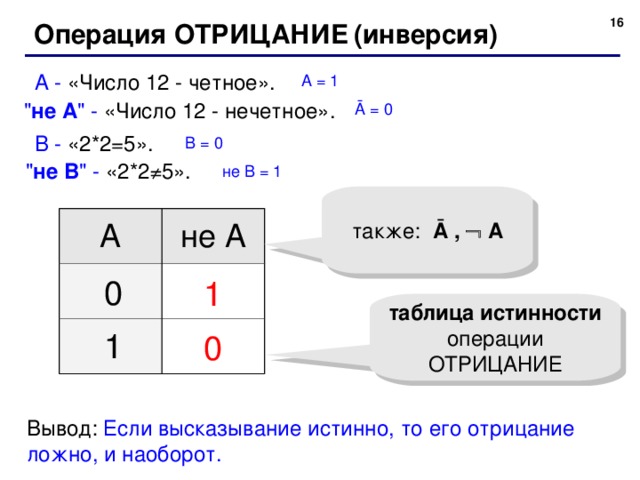
Операция ОТРИЦАНИЕ ( инверсия)
А - «Число 12 - четное».
А = 1
" не А " - «Число 12 - нечетное».
Ā = 0
В - «2*2=5».
В = 0
" не В " - «2*2 ≠ 5».
не В = 1
также: Ā , А
А
не А
0
1
таблица истинности операции ОТРИЦАНИЕ
1
0
Вывод: Если высказывание истинно, то его отрицание ложно, и наоборот.
Операция КОНЪЮНКЦИЯ ( логическое умножение)
конъюнкция – от лат. conjunctio — соединение
В естественном языке ей соответствует союз " и ".
Обозначение: A·B , A & B
А – "Число 10 - четное",
В – "Число 10 - отрицательное".
F (А,В) - " Число 10 – четное и отрицательное "
C – "Петр выучил уроки",
D – "Петр пошел гулять во двор".
F ( C , D ) - " Петр выучил уроки и пошел гулять во двор "
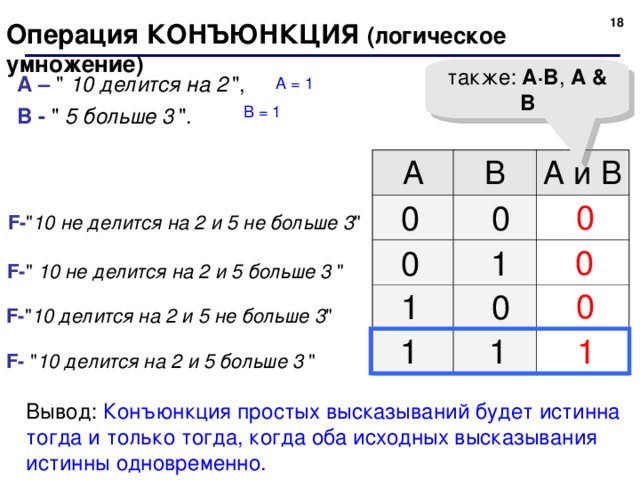
Операция КОНЪЮНКЦИЯ ( логическое умножение)
также: A·B , A & B
А – " 10 делится на 2 ",
В - " 5 больше 3 ".
А = 1
В = 1
A
B
А и B
0
0
0
F- " 10 не делится на 2 и 5 не больше 3 "
0
1
0
F- " 10 не делится на 2 и 5 больше 3 "
0
0
1
F- " 10 делится на 2 и 5 не больше 3 "
1
1
1
F- " 10 делится на 2 и 5 больше 3 "
Вывод: Конъюнкция простых высказываний будет истинна тогда и только тогда, когда оба исходных высказывания истинны одновременно.
18
18
Операция ДИЗЪЮНКЦИЯ ( логическое сложение)
дизъюнкция – от лат. dis junctio — разъединение
В естественном языке ей соответствует союз " или ".
Обозначение: A + B , A B
А – "Андрей старше Светы",
В – "Андрей старше Наташи".
F (А,В) - " Андрей старше Светы или Наташи "
C – "На полке стоят учебники",
D – "На полке стоят справочники".
F ( C , D ) - " На полке стоят учебники или справочники "
18
18
Операция ДИЗЪЮНКЦИЯ ( логическое сложение)
также: A + B , A B
А – "Число 10 - четное",
В - "Число 10 - отрицательное".
А = 1
В = 0
A
B
А или B
0
0
0
F- "Число 10 – не четное или отрицательное"
0
1
1
F- "Число 10–не четное или не отрицательное"
0
1
1
F- " Число 10–четное или отрицательное "
1
1
1
F- "Число 10–четное или не отрицательное"
Вывод: Дизъюнкция простых высказываний будет ложна тогда и только тогда, когда оба исходных высказывания ложны одновременно.
20
инверсии в естественном языке соответствует союз " не ".
Обозначение: Ā , А
конъюнкции в естественном языке соответствует союз " и ".
Обозначение: A·B , A & B
дизъюнкции в естественном языке соответствует союз " или ".
Обозначение: A + B , A B
20
F (А) – " Неверно, что корова – хищное животное",
F (А,В) – "Завтра будет ясная погода или выпадет снег",
F (А,В) - " Света и Наташа старше Андрея " ,
F (А,В) - " Петр поедет в деревню и пойдет на рыбалку",
F (А,В) – "Квадрат является прямоугольником и ромбом".
F (А,В) – "Я съем яблоко или апельсин".
20
20
- базовые логические операции – конъюнкция, дизъюнкция и отрицание.
- дополнительные логические операции – импликация и эквиваленция.
B , где A - условие , B - следствие А – "Работник хорошо работает", В – "У работника хорошая зарплата". F (А,В) - " Если работник хорошо работает, то у него хорошая зарплата " C – "Число делится на 10 ", D – "Число делится на 5". F ( C , D ) - " Если число делится на 10, то оно делится и на 5" 20 " width="640"
20
Операция ИМПЛИКАЦИЯ ( логическое следование)
импликация – от лат. implicatio – тесно связывать
В естественном языке ей соответствуют обороты
" если..., то.... ",
" из... следует.... "
Обозначение: A = B , где A - условие , B - следствие
А – "Работник хорошо работает",
В – "У работника хорошая зарплата".
F (А,В) - " Если работник хорошо работает, то у него хорошая
зарплата "
C – "Число делится на 10 ",
D – "Число делится на 5".
F ( C , D ) - " Если число делится на 10, то оно делится и на 5"
20
B F - "Данный четырёхугольник не является квадратом, и около него нельзя описать окружность " 1 0 0 F - "Данный четырёхугольник не является квадратом, но около него можно описать окружность " 1 1 0 F - "Данный четырёхугольник является квадратом, но около него нельзя описать окружность " 0 1 0 1 1 1 F - "Данный четырёхугольник квадрат, и около него можно описать окружность " Вывод: Импликация простых высказываний будет ложна тогда и только тогда, когда из истинного условия следует ложное следствие. 24 " width="640"
20
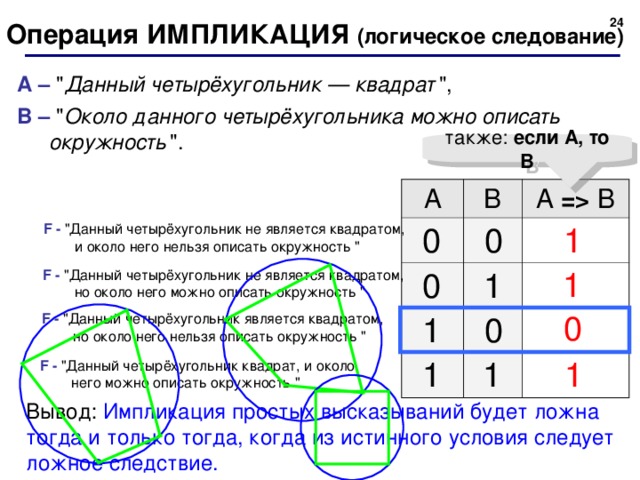
Операция ИМПЛИКАЦИЯ ( логическое следование)
А – " Данный четырёхугольник — квадрат ",
В – " Около данного четырёхугольника можно описать окружность ".
также: если A , то B
A
B
А = B
F - "Данный четырёхугольник не является квадратом, и около него нельзя описать окружность "
1
0
0
F - "Данный четырёхугольник не является квадратом, но около него можно описать окружность "
1
1
0
F - "Данный четырёхугольник является квадратом, но около него нельзя описать окружность "
0
1
0
1
1
1
F - "Данный четырёхугольник квадрат, и около него можно описать окружность "
Вывод: Импликация простых высказываний будет ложна тогда и только тогда, когда из истинного условия следует ложное следствие.
24
24
"Если президент США — демократ, то в Африке водятся жирафы",
"Если арбуз — ягода, то в бензоколонке есть бензин".
24
Операция ЭКВИВАЛЕНЦИЯ ( логическое равенство)
эквиваленция – от лат. aequivalens – равноценное
В естественном языке ей соответствуют обороты " тогда и только тогда ..., когда.... ", " необходимо и достаточно ", " ... равносильно.... "
Обозначение: А B или А B .
А – "Работник хорошо работает",
В – "У работника хорошая зарплата".
F (А,В) - "Работник хорошо работает, тогда и только тогда, когда у него хорошая зарплата "
C – "Число четное ",
D – "Число делится на 2".
F ( C , D ) - "Число будет четным, тогда и только тогда, когда оно делится на 2"
24
24
Операция ЭКВИВАЛЕНЦИЯ ( логическое равенство)
также: A т.т.т, к. B
А – " Число делится на 6 ",
В – " Число делится на 3 ".
A
B
А B
F- "23 делится на 6 тогда и только тогда, когда 23 делится на 3"
0
0
1
F- "21 делится на 6 тогда и только тогда, когда 21 делится на 3"
0
1
0
F- "24 делится на 6 тогда и только тогда, когда 24 делится на 5"
0
1
0
1
1
F- "24 делится на 6 тогда и только тогда, когда 24 делится на 3"
1
Вывод: Эквиваленция простых высказываний будет истинна тогда и только тогда, когда оба исходных высказывания истинны или ложны одновременно.
27
В = Ā v В. Эквиваленцию можно выразить через отрицание , дизъюнкцию и конъюнкцию : А В = ( Ā v В) & ( ¬B v А). А В = ( Ā v В) & ( ¬B v А). А В = ( Ā v В) & ( ¬B v А). А В = ( Ā v В) & ( ¬B v А). А В = ( Ā v В) & ( ¬B v А). ? ? " width="640"
27
Итак, нами рассмотрены пять логических операций:
- отрицание, конъюнкция, дизъюнкция, Импликация, эквиваленция.
- отрицание, конъюнкция, дизъюнкция, Импликация, эквиваленция.
- отрицание, конъюнкция, дизъюнкция, Импликация, эквиваленция.
- отрицание,
- конъюнкция,
- дизъюнкция,
- Импликация,
- эквиваленция.
Импликацию можно выразить через дизъюнкцию и отрицание:
А = В = Ā v В.
Эквиваленцию можно выразить через отрицание , дизъюнкцию и конъюнкцию :
А В = ( Ā v В) & ( ¬B v А).
- А В = ( Ā v В) & ( ¬B v А).
- А В = ( Ā v В) & ( ¬B v А).
- А В = ( Ā v В) & ( ¬B v А).
- А В = ( Ā v В) & ( ¬B v А).
?
?
, & , ¬ , ( ), " width="640"
Порядок выполнения логических операций
27
v,
= ,
& ,
¬ ,
( ),
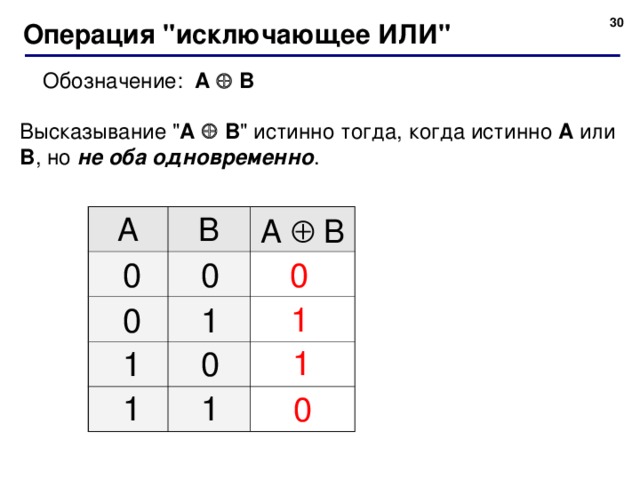
Операция " исключающее ИЛИ "
Обозначение: A B
Высказывание " A B " истинно тогда, когда истинно А или B , но не оба одновременно .
A
B
А B
0
0
0
1
0
1
1
1
0
1
1
0
30
30
Тема 2. Таблицы истинности
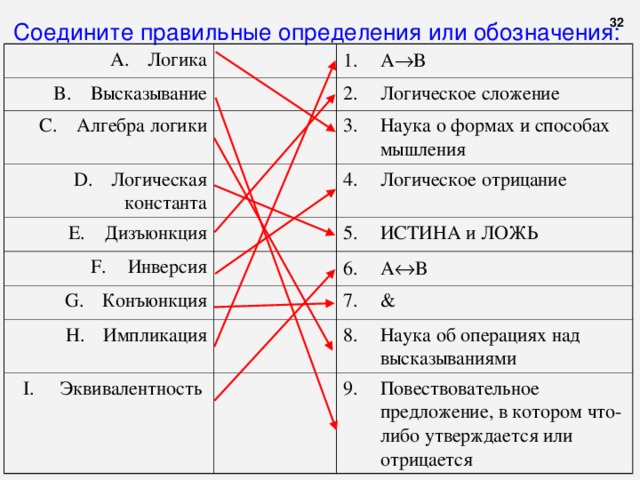
Соедините правильные определения или обозначения:
30
- Наука о формах и способах мышления
- Наука об операциях над высказываниями
- Повествовательное предложение, в котором что-либо утверждается или отрицается
Если верно 8,9 ответов – «5»
Если верно 6,7 ответов – «4»
Если верно 4,5 ответов – «3»
Даны высказывания: А – “ 3*3=9 ” ,
В – “ 3*3=10 ”
Определите истинность высказываний:
1) А,
2) В,
3) A & B ,
4) В,
5) А,
6) А В.
- 1) А, 2) В, 3) A & B , 4) В, 5) А, 6) А В.
- 1) А, 2) В, 3) A & B , 4) В, 5) А, 6) А В.
- 1) А, 2) В, 3) A & B , 4) В, 5) А, 6) А В.
1
1
0
0
0
1
Найдите значение логического выражения:
0 ν =(0,0)
- l ) F = (0 v 0) v (1 v 0).
Решение: F = (0 v 0) v (1 v 0)= (0) v (1)=
=0 v 1=1.
1 & =( 1 , 1 )
- 2 ) F = (0 & 0) v ( 0&1 ).
Решение: F = (0 & 0) v ( 0&1 )= (0) v ( 1&1 )=
=0 v 1=1.
Найдите значения логических выражений:
3 ) F = (1 & 0) & ( 0v 1).
4 ) F = (0&0)&(1&1).
5 ) F = 0 &( 0v 1) v ( 1 & 0 ).
6 ) F = ( 0 & 1)&(1 v 1)&( 0 v 0).
Логические формулы
Система имеет три датчика и может работать, если два из них исправны.
A – " Датчик № 1 неисправен".
B – "Датчик № 2 неисправен".
C – "Датчик № 3 неисправен".
Аварийный сигнал :
X – "Неисправны два датчика".
X – "Неисправны датчики № 1 и № 2" или
"Неисправны датчики № 1 и № 3" или
"Неисправны датчики № 2 и № 3".
логическая формула
37
37
37
Алгоритм составления таблицы истинности :
- Выяснить количество строк в таблице (вычисляется как 2 n , где n – количество переменных).
- Выяснить количество столбцов = количество переменных + количество логических операций.
- Установить последовательность выполнения логических операций.
- Построить таблицу , указывая названия столбцов и возможные наборы значений исходных логических переменных.
- Заполнить таблицу истинности по столбцам.
Пример 1: F =( A B )&( A B ).
37
Пример 1: F =( A B )&( A B ).
Пример 1: F =( A B )&( A B ).
- Количество строк = 2 2 =4 (2 переменных)
- Количество столбцов =2+5=7(2 логические переменные (А, В), 5 логических операций ,&, , , .
- Расставим порядок выполнения операций: ( A B ) & ( A B )
1
5
2
4
3
Пример 1: F =( A B )&( A B ).
- Количество строк = 2 2 =4 (2 переменных)
- Количество столбцов =2+5=7(2 логические переменные (А, В), 5 логических операций ,&, , , .
- Расставим порядок выполнения операций: ( A B ) & ( A B )
- Построим таблицу и заполним ее по столбцам:
1
5
2
4
3
3
1
4
2
5
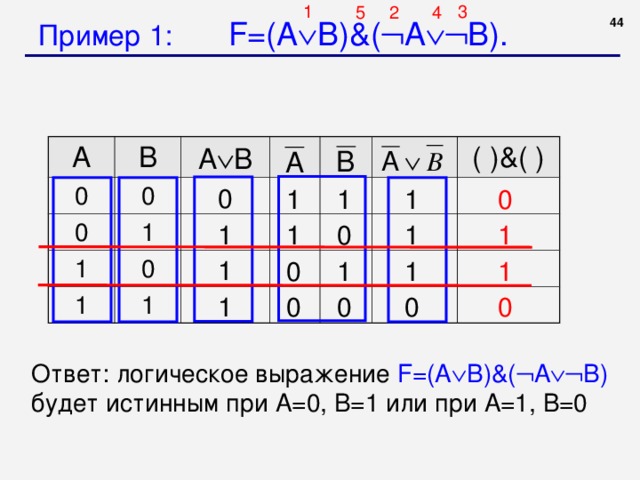
Пример 1: F =( A B )&( A B ).
A
B
0
0
A B
0
1
1
1
0
1
( ) &( )
0
0
1
1
1
1
1
1
0
1
1
1
1
0
1
1
0
0
0
0
Ответ: логическое выражение F =( A B )&( A B ) будет истинным при А=0, В=1 или при А=1, В=0
44
Алгоритм составления таблицы истинности :
- Выяснить количество строк в таблице (вычисляется как 2 n , где n – количество переменных).
- Выяснить количество столбцов = количество переменных + количество логических операций.
- Установить последовательность выполнения логических операций.
- Построить таблицу , указывая названия столбцов и возможные наборы значений исходных логических переменных.
- Заполнить таблицу истинности по столбцам.
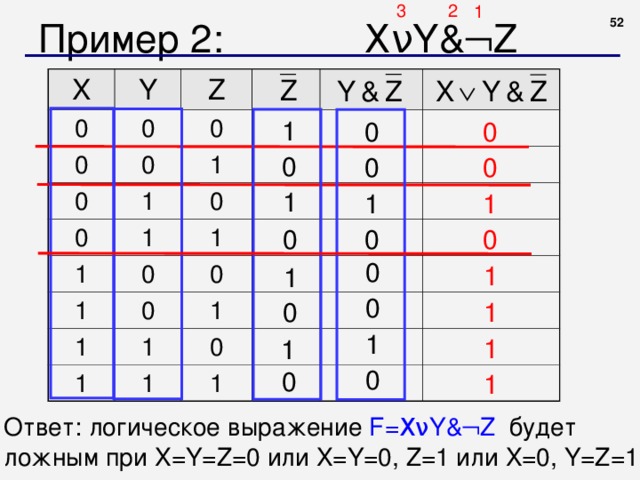
Пример 2: X ν Y & Z
44
- Количество строк =2 3 =8.
Пример 2: X ν Y & Z
Пример 2: X ν Y & Z
- Количество строк =2 3 =8.
- Количество столбцов =3+3=6 (3 логические переменные+3 логических операции).
- Укажем порядок действий: X ν Y & Z
3
2
1
Пример 2: X ν Y & Z
- Количество строк =2 3 =8.
- Количество столбцов =3+3=6 (3 логические переменные+3 логических операции).
- Укажем порядок действий: X ν Y & Z
- Нарисуем и заполним таблицу:
3
2
1
- Кол-во строк в таблице при n =3
Наборы входных переменных, во избежание ошибок, рекомендуется перечислять следующим образом:
а) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;
б) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц, начиная с группы нулей;
в) продолжать деление колонок значений последующих переменных на 8, 16 и так далее частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.
3
2
1
Пример 2: X ν Y & Z
X
Y
0
Z
0
0
0
0
0
1
1
0
0
1
1
1
0
1
0
0
1
1
1
1
0
1
1
1
0
0
0
0
0
1
1
1
0
0
0
0
1
1
0
1
0
1
1
1
0
0
1
Ответ: логическое выражение F = X ν Y & Z будет ложным при X = Y=Z= 0 или X=Y=0, Z =1 или X=0, Y=Z =1
Логические формулы
Система имеет три датчика и может работать, если два из них исправны.
A – " Датчик № 1 неисправен".
B – "Датчик № 2 неисправен".
C – "Датчик № 3 неисправен".
Аварийный сигнал :
X – "Неисправны два датчика".
X – "Неисправны датчики № 1 и № 2" или
"Неисправны датчики № 1 и № 3" или
"Неисправны датчики № 2 и № 3".
логическая формула
53
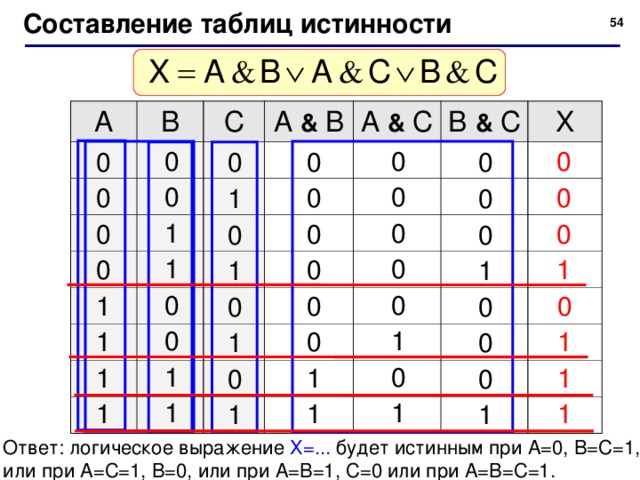
Составление таблиц истинности
53
A
B
C
A & B
A & C
B & C
X
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
1
1
0
0
1
1
0
0
0
1
0
0
0
1
0
1
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
1
Ответ: логическое выражение Х=... будет истинным при А=0, В=С=1, или при А=С=1, В=0, или при А=В=1, С=0 или при А=В=С=1.
54
54
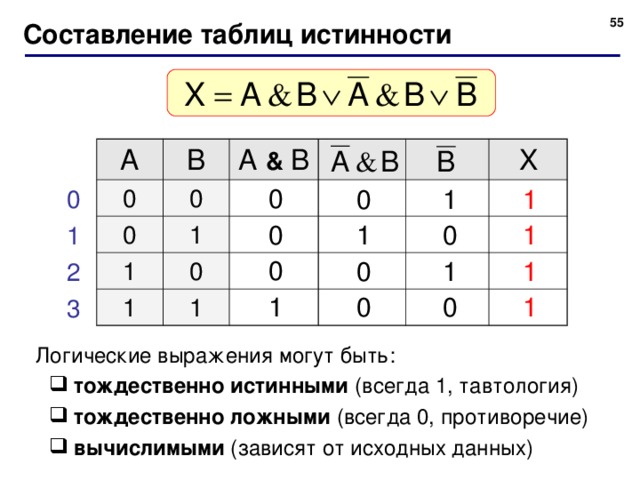
Составление таблиц истинности
A
B
0
0
A & B
0
1
1
0
1
1
X
0
1
1
0
0
1
2
3
0
1
0
1
0
0
1
1
1
0
0
1
Логические выражения могут быть:
- тождественно истинными (всегда 1, тавтология) тождественно ложными (всегда 0, противоречие) вычислимыми (зависят от исходных данных)
- тождественно истинными (всегда 1, тавтология)
- тождественно ложными (всегда 0, противоречие)
- вычислимыми (зависят от исходных данных)
55
55
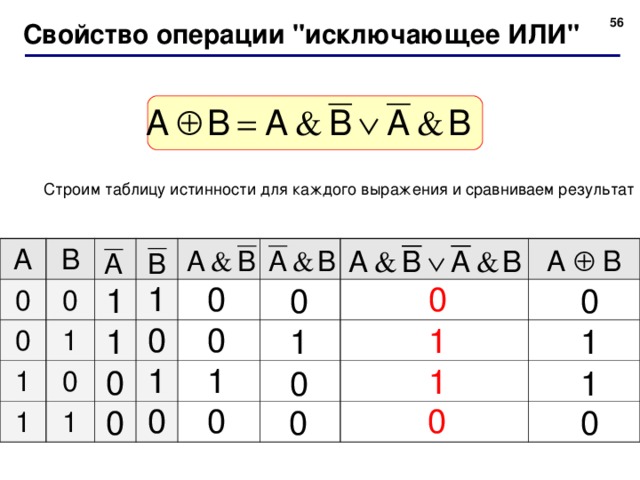
Свойство операции " исключающее ИЛИ "
Строим таблицу истинности для каждого выражения и сравниваем результат
A
B
0
0
0
1
1
1
0
1
А B
0
1
0
0
0
1
0
0
1
1
1
1
1
1
1
0
1
0
0
0
0
0
0
0
56
56
Тема 3. Логические элементы компьютера
56
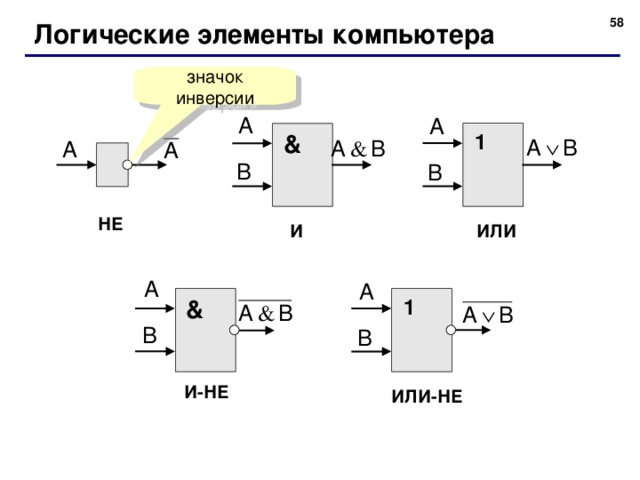
Логические элементы компьютера
значок инверсии
&
1
НЕ
И
ИЛИ
&
1
И-НЕ
ИЛИ-НЕ
58
58
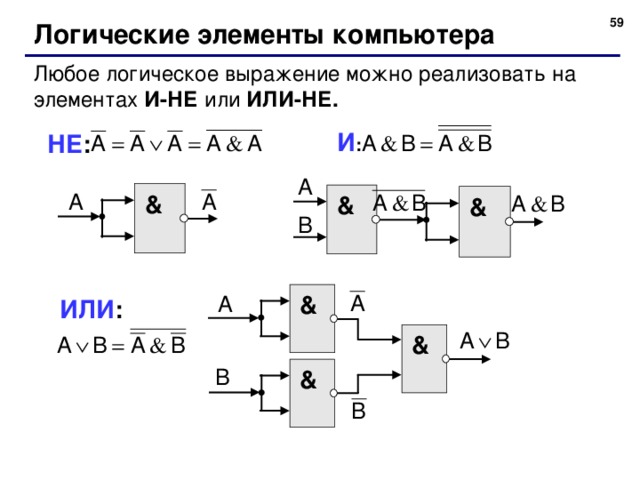
Логические элементы компьютера
Любое логическое выражение можно реализовать на элементах И-НЕ или ИЛИ-НЕ.
И :
НЕ :
&
&
&
&
ИЛИ :
&
&
59
59
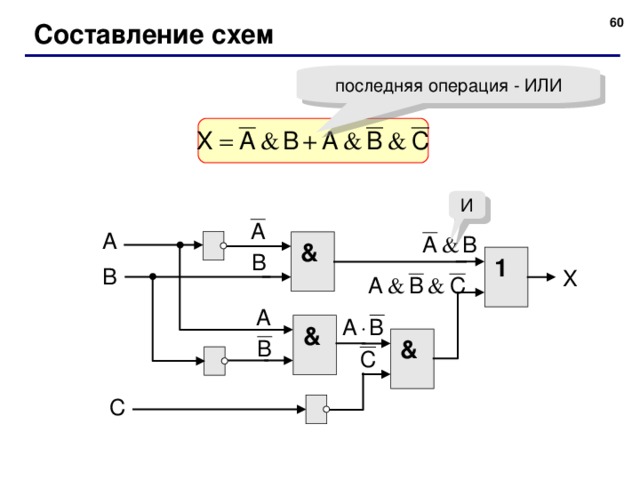
Составление схем
последняя операция - ИЛИ
И
&
1
&
&
60
60
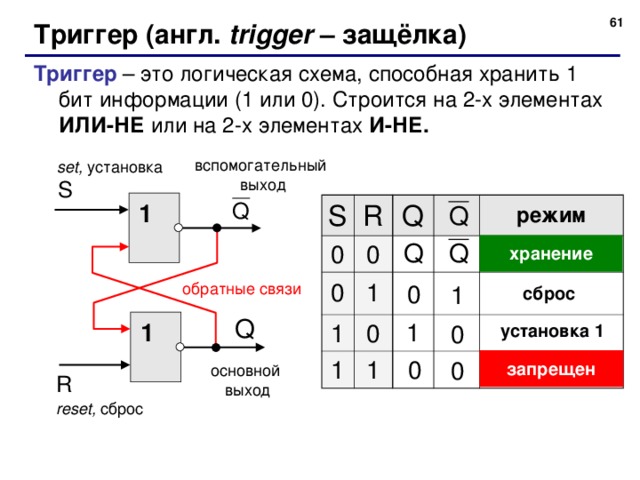
Триггер (англ. trigger – защёлка)
Триггер – это логическая схема, способная хранить 1 бит информации (1 или 0). Строится на 2-х элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
вспомогательный
выход
set, установка
1
S
R
0
Q
0
0
1
1
0
1
режим
1
хранение
обратные связи
0
сброс
1
установка 1
1
1
0
запрещен
0
0
основной
выход
reset, сброс
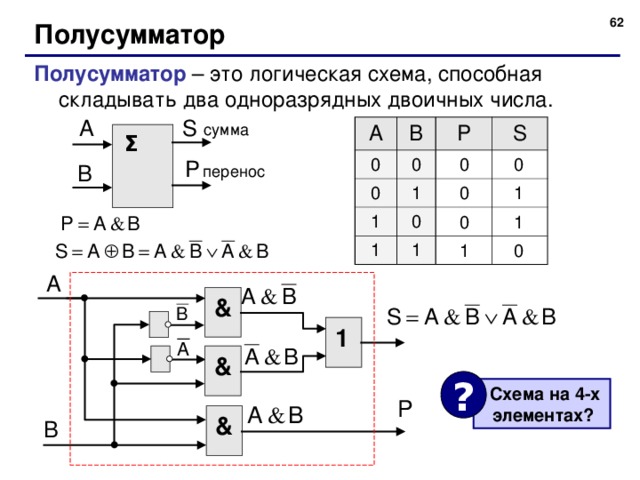
Полусумматор
Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа.
сумма
A
B
0
0
P
0
1
1
S
0
1
1
Σ
0 0
перенос
0 1
0 1
1 0
&
1
&
?
Схема на 4-х элементах?
&
62
62
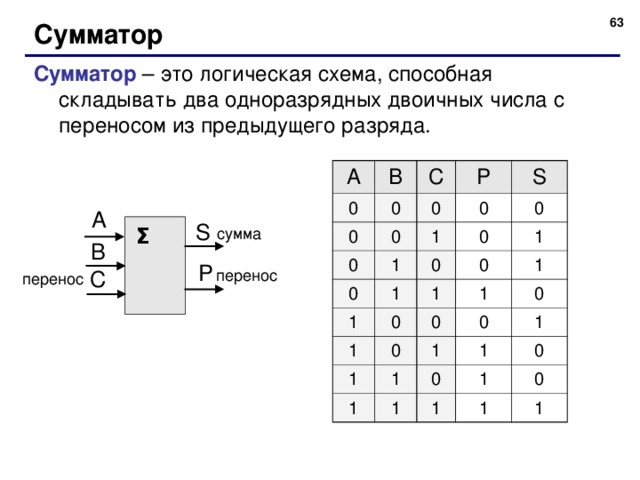
Сумматор
Сумматор – это логическая схема, способная складывать два одноразрядных двоичных числа с переносом из предыдущего разряда.
A
B
0
0
C
0
P
0
0
0
1
0
0
1
S
0
1
1
0
0
0
1
1
0
1
1
0
1
1
0
0
1
1
0
1
1
1
0
1
0
1
1
1
0
1
Σ
сумма
перенос
перенос
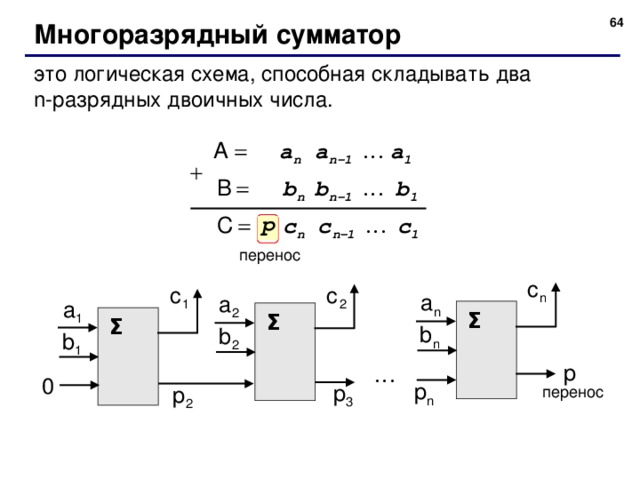
Многоразрядный сумматор
это логическая схема, способная складывать два n- разрядных двоичных числа.
перенос
Σ
Σ
Σ
перенос
64
64
Тема 4. Логические задачи
64
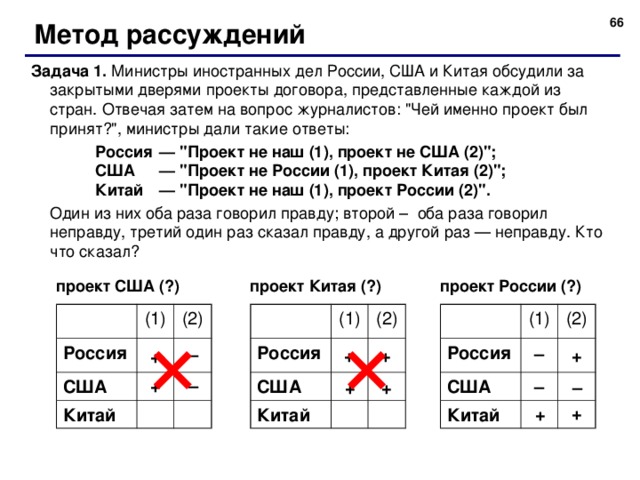
Метод рассуждений
Задача 1. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты договора, представленные каждой из стран. Отвечая затем на вопрос журналистов: "Чей именно проект был принят?", министры дали такие ответы:
Россия — "Проект не наш (1) , проект не США (2) ";
США — "Проект не России (1) , проект Китая (2) ";
Китай — "Проект не наш (1) , проект России (2) ".
Один из них оба раза говорил правду; второй – оба раза говорил неправду, третий один раз сказал правду, а другой раз — неправду. Кто что сказал?
проект России ( ?)
проект Китая ( ?)
проект США ( ?)
Россия
Россия
Россия
(1)
(1)
(1)
(2)
(2)
(2)
США
США
США
Китай
Китай
Китай
–
–
+
+
+
+
+
–
–
–
+
+
+
+
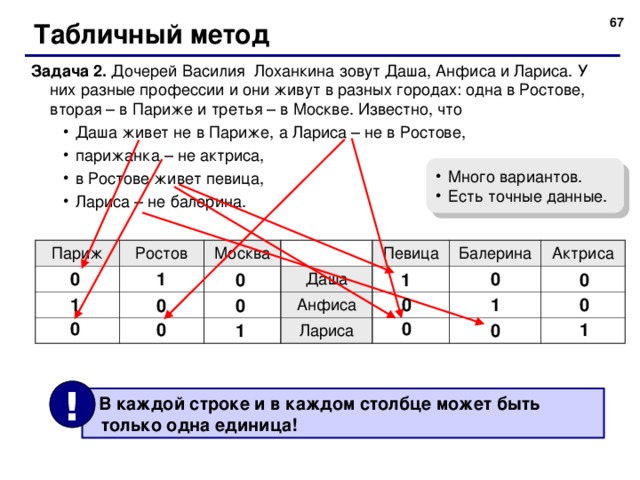
Табличный метод
Задача 2. Дочерей Василия Лоханкина зовут Даша, Анфиса и Лариса. У них разные профессии и они живут в разных городах: одна в Ростове, вторая – в Париже и третья – в Москве. Известно, что
- Даша живет не в Париже, а Лариса – не в Ростове, парижанка – не актриса, в Ростове живет певица, Лариса – не балерина.
- Даша живет не в Париже, а Лариса – не в Ростове,
- парижанка – не актриса,
- в Ростове живет певица,
- Лариса – не балерина.
- Много вариантов.
- Есть точные данные.
Париж
Ростов
Москва
Певица
Даша
Балерина
Анфиса
Актриса
Лариса
0
1
0
1
0
0
0
1
0
1
0
0
0
0
1
0
0
1
!
В каждой строке и в каждом столбце может быть только одна единица!
67
67
Задача Эйнштейна
Условие: Есть 5 домов разного цвета, стоящие в ряд. В каждом доме живет по одному человеку отличной от другого национальности. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит животное. Никто из пяти человек не пьет одинаковые напитки, не курит одинаковые сигареты и не держит одинаковых животных.
Известно, что:
- Англичанин живет в красном доме. Швед держит собаку. Датчанин пьет чай. Зеленой дом стоит слева от белого. Жилец зеленого дома пьет кофе. Человек, который курит Pallmall , держит птицу. Жилец среднего дома пьет молоко. Жилец из желтого дома курит Dunhill . Норвежец живет в первом доме. Курильщик Marlboro живет около того, кто держит кошку. Человек, который содержит лошадь, живет около того, кто курит Dunhill . Курильщик Winfield пьет пиво. Норвежец живет около голубого дома. Немец курит Rothmans . Курильщик Marlboro живет по соседству с человеком, который пьет воду.
- Англичанин живет в красном доме.
- Швед держит собаку.
- Датчанин пьет чай.
- Зеленой дом стоит слева от белого.
- Жилец зеленого дома пьет кофе.
- Человек, который курит Pallmall , держит птицу.
- Жилец среднего дома пьет молоко.
- Жилец из желтого дома курит Dunhill .
- Норвежец живет в первом доме.
- Курильщик Marlboro живет около того, кто держит кошку.
- Человек, который содержит лошадь, живет около того, кто курит Dunhill .
- Курильщик Winfield пьет пиво.
- Норвежец живет около голубого дома.
- Немец курит Rothmans .
- Курильщик Marlboro живет по соседству с человеком, который пьет воду.
Вопрос: У кого живет рыба?
67
67
Использование алгебры логики
Задача 3. Следующие два высказывания истинны:
1. Неверно, что если корабль A вышел в море, то корабль C – нет.
2. В море вышел корабль B или корабль C , но не оба вместе.
- 1. Неверно, что если корабль A вышел в море, то корабль C – нет. 2. В море вышел корабль B или корабль C , но не оба вместе.
Определить, какие корабли вышли в море.
Решение:
… если корабль A вышел в море, то корабль C – нет.
1. Неверно, что если корабль A вышел в море, то корабль C – нет.
2. В море вышел корабль B или корабль C , но не оба вместе.
69
69
Использование алгебры логики
Задача 4. Когда сломался компьютер, его хозяин сказал «Память не могла выйти из строя». Его сын предположил, что сгорел процессор, а винчестер исправен. Мастер по ремонту сказал, что с процессором все в порядке, а память неисправна. В результате оказалось, что двое из них сказали все верно, а третий – все неверно. Что же сломалось?
Решение:
A – неисправен процессор, B – память, C – винчестер
сын:
мастер:
хозяин:
Если ошибся хозяин:
Если ошибся сын:
Если ошибся мастер:
!
Несколько решений!
В общем случае:
70
Получите свидетельство
Вход
Основы логики (2.65 MB)
0
1386
38
Нравится
0
