Получите свидетельство
Вход
ПОДГОТОВКА К ЕГЭ ПО ИНФОРМАТИКЕ
Тема «Основы логики»
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ
Логика – наука о формах и способах мышления. Основными формами мышления являются понятие , суждение , умозаключение .
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними.
Высказывание может быть либо истинно , либо ложно .
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (вывод).
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ
ЛОГИКИ
Л огик а — это наука, изучающая законы и формы мышления.
Алгебра логики — это математическ ий аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логи ческие высказывания.
Высказывание — это повествовательное предложение, о которо м можно сказать, истинно оно или ложно. При этом считается, что высказывание удовлетворяет закону исключенного третьего, т.е. каждое высказывание или истинно, или ложно и не может быть одновременно и истинным, и ложным.
Если высказывание :
и стинно - его значение равно 1 (True, T) ;
ложно - 0 (False, F) .
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ
Высказывание не может быть выражено повелительным или вопросительным предложением , так как оценка их истинности или ложности невозможна.
Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок И, ИЛИ и частицей НЕ . Значение истинности сложных высказываний зависит от истинности входящих в них простых высказываний и объединяющих их связок.
В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно .
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ
Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть 0 или 1 .
Если высказывание :
истинно - его значение равно 1 (True, T) ,
ложно - 0 (False, F) .
Простые высказывания назвали логическими переменными , а сложные высказывания логическими функциями . Значения логической функции также только 0 или 1. Для простоты записи высказывания обозначаются латинскими буквами А, В, С.
Пример простых высказыв а ний:
A = “2+2=4” – истинно,
B = “Земля не вертится” – ложно.
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
В основе булевой алгебры лежат 16 основных функций. Наиболее часто применяемые из них:
- л огическое отрицание (инверсия) – « не »; ¬ ; ¯ ;
- л огическое отрицание (инверсия) – « не »; ¬ ; ¯ ;
- л огическое умножение (конъюнкция) – « и »; & ; ^ ; • ;
- л огическое сложение (дизъюнкция) – « или »; + ; ;
- л огическое следование (импликация) –
- л огическая операция эквивалентности – ~ ; ; ;
- ф ункция Вебба (отрицание дизъюнкции) – ИЛИ-НЕ ;
- ф ункция Шеффера (отрицание конъюнкции) – И-НЕ ;
- с ложение по модулю 2 (М2) .
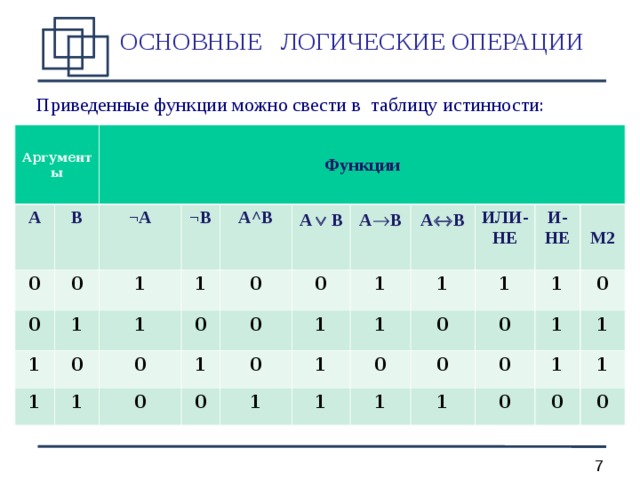
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Приведенные функции можно свести в таблицу истинности:
Аргументы
A
Функции
B
0
0
0
¬ A
1
1
1
¬B
1
0
1
A ^B
1
0
1
A B
0
0
0
1
0
0
A B
A B
1
0
1
0
1
1
1
1
ИЛИ-НЕ
0
1
0
1
И-НЕ
0
1
1
0
М2
1
0
0
1
1
1
0
1
0
0
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
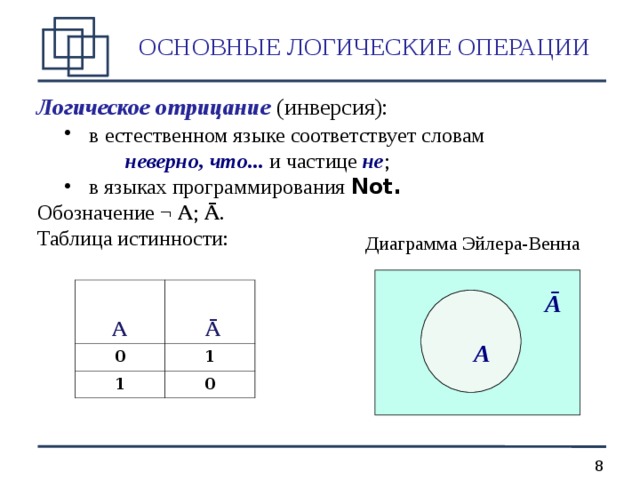
Логическое отрицание (инверсия):
- в естественном языке соответствует словам
- в естественном языке соответствует словам
неверно, что... и частице не ;
- неверно, что... и частице не ;
- в языках программирования Not .
- в языках программирования Not .
Обозначение ¬ A ; Ā .
Таблица истинности:
Диаграмма Эйлера-Венна
A
0
Ā
1
1
0
Ā
A
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
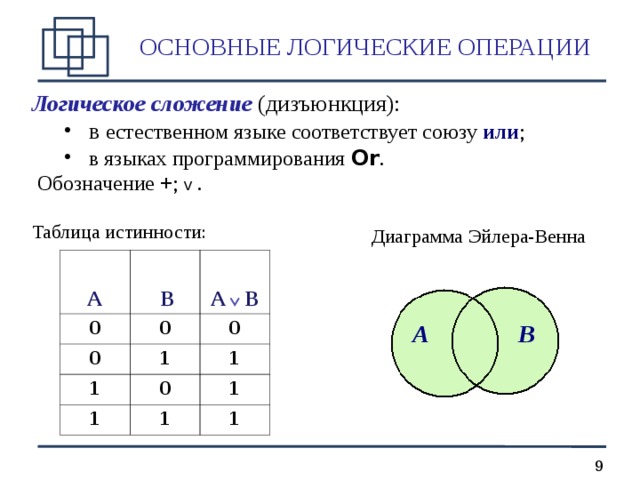
Логическое сложение (дизъюнкция):
- в естественном языке соответствует союзу или ; в языках программирования Or .
- в естественном языке соответствует союзу или ;
- в языках программирования Or .
Обозначение + ; v .
Таблица истинности:
Диаграмма Эйлера-Венна
A
0
B
0
A B
0
0
1
1
1
1
0
1
1
1
A
B
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
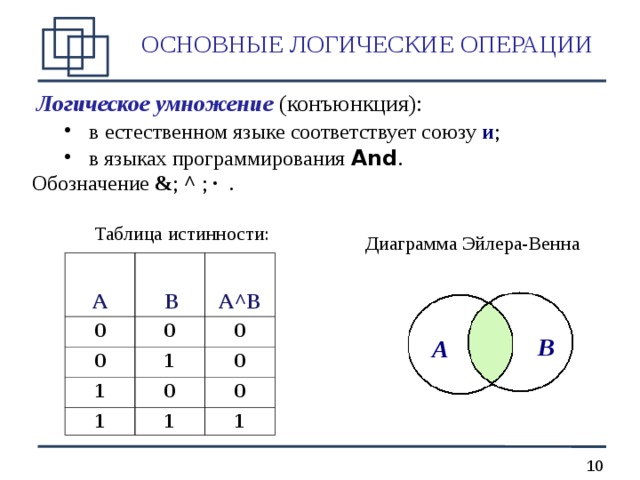
Логическое умножение (конъюнкция):
- в естественном языке соответствует союзу и ; в языках программирования And .
- в естественном языке соответствует союзу и ;
- в языках программирования And .
Обозначение & ; ^ ; ∙ .
Таблица истинности:
Диаграмма Эйлера-Венна
A
0
B
0
A ^B
0
0
1
1
1
0
0
0
- 0
1
1
B
A
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
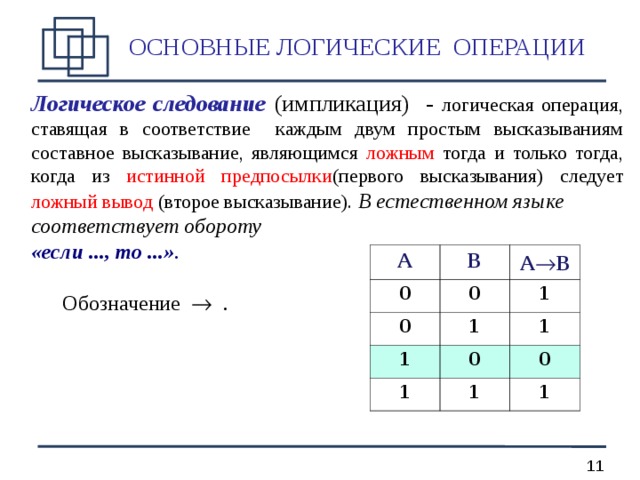
Логическое следование (импликация) - логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющимся ложным тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание). В естественном языке
соответствует обороту
« если ..., то ... » .
Обозначение .
A
0
B
A B
0
0
1
1
1
1
1
0
0
1
1
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
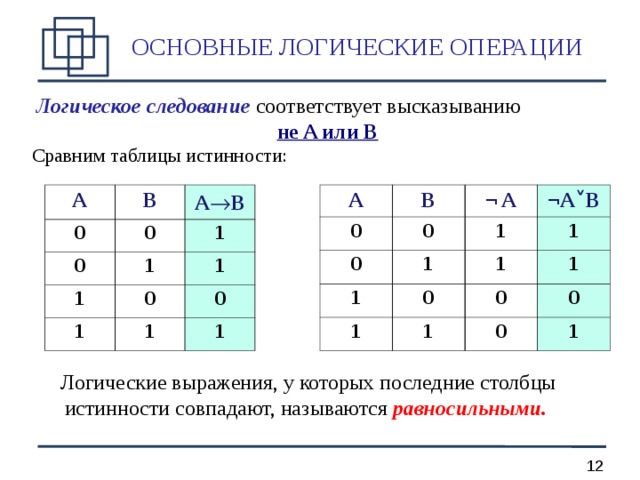
Логическое следование соответствует высказыванию
не A или B
Сравним таблицы истинности:
A
B
A
0
0
0
B
A B
0
1
0
1
¬ A
1
0
1
1
¬ A ˅B
1
1
1
0
0
1
1
0
1
1
1
0
1
1
0
0
1
Логические выражения, у которых последние столбцы истинности совпадают, называются равносильными.
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
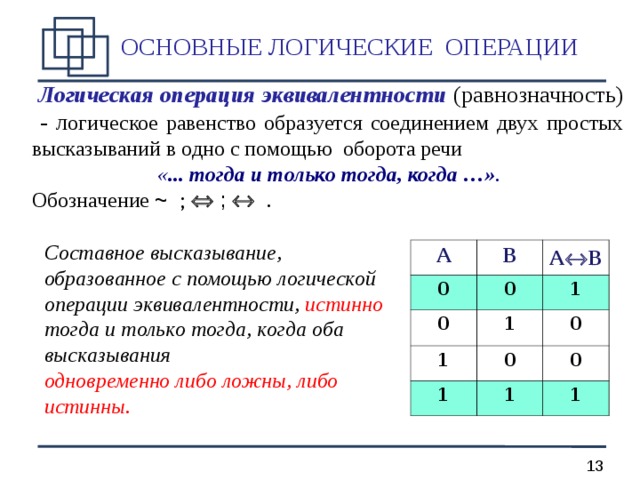
Логическая операция эквивалентности (равнозначность) - л огическое равенство образуется соединением двух простых высказываний в одно с помощью оборота речи
« ... тогда и только тогда, когда … » .
Обозначение ~ ; ; .
Составное высказывание, образованное с помощью логической операции эквивалентности , истинно
тогда и только тогда, когда оба высказывания
одновременно либо ложны, либо истинны.
A
0
B
0
0
A B
1
1
1
1
0
0
0
1
1
ПРИОРИТЕТ ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
- Логическое отрицание (инверсия) – « не »; ¬ ; ¯ .
- Логическое умножение (конъюнкция) – « и »; & ; ^ ; ∙ .
- Логическое сложение (дизъюнкция) – « или »; + ; .
- Логическое следование (импликация) –
- Логическая операция эквивалентности – ~ ; ; .
Для изменения указанного порядка могут использоваться скобки.
ТАБЛИЦЫ ИСТИННОСТИ
Т аблица истинности определяет истинность или ложность логической функции при всех возможных комбинациях исходных значений простых высказываний.
Правила построения таблиц истинности.
- Подсчитать количество переменных n в логическом выражении.
- Определить количество строк в таблице, которое равно m=2 n
- Подсчитать количество операций в логическом выражении и определить количество столбцов в таблице: k = количество переменных (n) + количество операций.
- Ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов.
- Заполнить столбцы логических переменных наборами значений.
- Провести заполнение таблицы истинности по столбцам, выполняя базовые логические операции в соответствии с установленной в п. 4 последовательностью.
ТАБЛИЦЫ ИСТИННОСТИ
Пример. Определить истинность формулы F=((C B) B) ^ (A ^ B) B
Формула является тождественно истинной , если все значения строк результирующего столбца будут равны 1 .
1 шаг. Определяем количество строк в таблице: m=2 3 =8
2 шаг. Определяем количество столбцов в таблице:
k=3+5=8
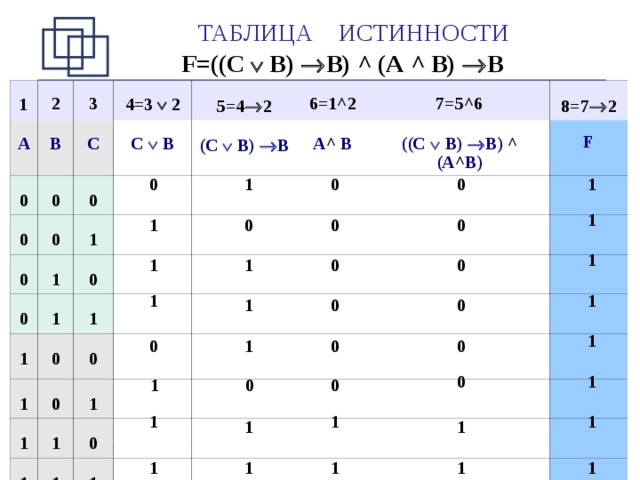
ТАБЛИЦА ИСТИННОСТИ F=((C B) B) ^ (A ^ B) B
2
A
3
B
0
C
4=3 2
0
0
C B
5=4 2
0
0
0
6=1 ^2
(C B) B
0
1
1
A ^ B
7=5 ^6
1
1
0
8=7 2
((C B) B) ^ (A ^ B)
1
0
1
F
1
0
0
1
1
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
1
1
0
0
1
1
0
0
1
1
0
0
1
0
0
1
1
0
0
1
1
1
1
1
1
1
1
1
1
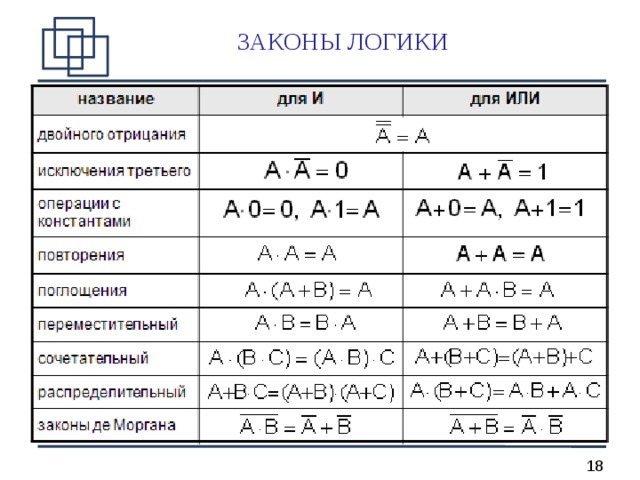
ЗАКОНЫ ЛОГИКИ
2)→(X 3)) ? 1) 1 2) 2 3) 3 4) 4 " width="640"
A 7 (повышенный уровень, время – 3 мин)
Для какого из указанных значений X истинно высказывание
¬((X 2)→(X 3)) ?
1) 1 2) 2 3) 3 4) 4
2)→(X 3)) " width="640"
Решение (Вариант 1. Прямая подстановка)
- Определим порядок действий: сначала вычисляются результаты отношений в скобках, затем выполняется импликация (поскольку есть «большие» скобки), затем – отрицание (операция «НЕ») для выражения в больших скобках.
¬((X 2)→(X 3))
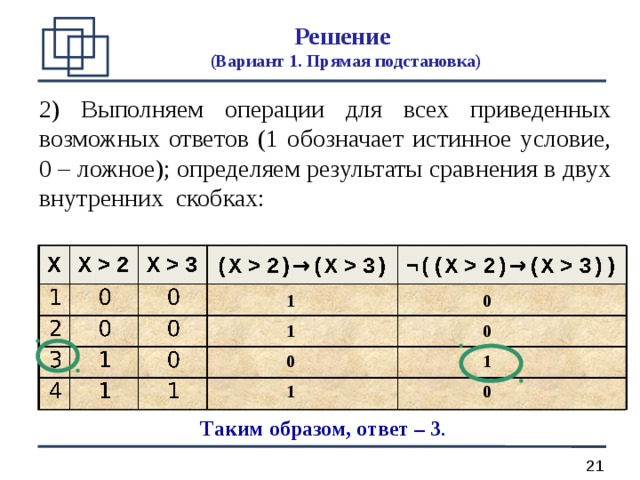
Решение (Вариант 1. Прямая подстановка)
2) Выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); определяем результаты сравнения в двух внутренних скобках:
1
0
1
0
0
1
1
0
Таким образом, ответ – 3 .
Возможные ловушки и проблемы
- Можно «забыть» отрицание (помните, что правильный ответ – всего один!)
- Можно перепутать порядок операций (скобки, «НЕ», «И», «ИЛИ», «импликация»)
- Нужно помнить таблицу истинности операции «импликация», которую очень любят составители тестов.
- Этот метод проверяет только заданные числа и не дает общего решения, то есть не определяет все множество значений X, при которых выражение истинно.
2)→(X 3)) Обозначим простые высказывания буквами: A = X 2 , B = X 3 Тогда можно записать все выражение в виде: ¬( A → B ) или Выразим импликацию через «НЕ» и «ИЛИ»: A → B = ¬ A + B = ¬ A B или Раскрывая по формуле де Моргана, получаем: ¬(¬ A B )= A ¬ B или Таким образом, данное выражение истинно только тогда, когда A истинно (X 2) , а B – ложно (X ≤ 3) , то есть для всех X , таких что 2 X ≤ 3 Таким образом, ответ – 3. " width="640"
Решение (Вариант 2. Упрощение выражения) ¬((X 2)→(X 3))
- Обозначим простые высказывания буквами:
A = X 2 , B = X 3
- Тогда можно записать все выражение в виде:
¬( A → B ) или
- Выразим импликацию через «НЕ» и «ИЛИ»:
A → B = ¬ A + B = ¬ A B или
- Раскрывая по формуле де Моргана, получаем:
¬(¬ A B )= A ¬ B или
- Таким образом, данное выражение истинно только тогда, когда A истинно (X 2) , а B – ложно (X ≤ 3) ,
то есть для всех X , таких что 2 X ≤ 3
Таким образом, ответ – 3.
3 является X ≤ 3 , а не X " width="640"
Возможные проблемы
- Нужно помнить законы логики (например, формулы де Моргана).
- При использовании формул де Моргана нужно не забыть заменить «И» на «ИЛИ» и наоборот.
- Нужно не забыть, что инверсией (отрицанием) для выражения X 3 является X ≤ 3 , а не X
Выводы
- В данном случае, наверное, проще первый вариант решения (прямая подстановка всех предложенных ответов).
- Второй вариант позволяет не только проверить заданные значения, но и получить общее решение – все множество X , для которых выражение истинно; это более красиво для человека, обладающего математическим складом ума.
A 8 (базовый уровень, время – 1 мин)
Решение (Вариант 1. Использование законов де Моргана)
- Перепишем заданное выражение в других обозначениях: A ¬(¬B C) =
- Применим формулу де Моргана, а затем закон двойного отрицания:
- Перепишем ответы в других обозначениях:
- ¬A ¬B ¬C = A ¬B ¬C = A B ¬C = A ¬B C =
- ¬A ¬B ¬C =
- A ¬B ¬C =
- A B ¬C =
- A ¬B C =
- Таким образом, правильный ответ – 3 .
Возможные ловушки и проблемы
- Серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений, поэтому рекомендуется сначала внимательно перевести их в удобный вид; потом сразу становится понятно.
- При использовании законов де Моргана часто забывают, что нужно заменить «И» на «ИЛИ» и «ИЛИ» на «И».
- Иногда для решения нужно упростить не только исходное выражение, но и заданные ответы, если они содержат импликацию или инверсию сложных выражений.
Решение (Вариант 2. Через таблицы истинности, если забыли формулы де Моргана)
- Перепишем заданное выражение в других обозначениях: A ¬(¬B C) =
- Перепишем ответы в других обозначениях:
- ¬A ¬B ¬C = A ¬B ¬C = A B ¬C = A ¬B C =
- ¬A ¬B ¬C =
- A ¬B ¬C =
- A B ¬C =
- A ¬B C =
- Для доказательства равносильности двух логических выражений достаточно показать, что они принимают равные значения при всех возможных комбинациях исходных данных.
Решение (Вариант 2. Продолжение)
- Поэтому можно составить таблицы истинности для исходного выражения и всех ответов и сравнить их.
- Здесь 3 переменных, каждая из которых принимает два возможных значения (всего 8 вариантов).
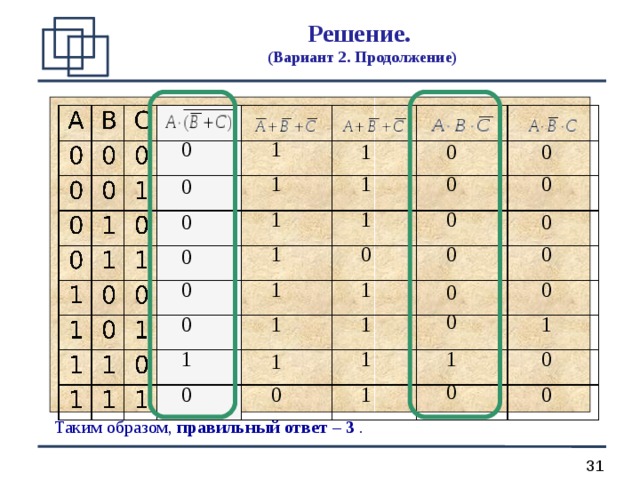
Решение. (Вариант 2. Продолжение)
0
1
0
1
0
1
0
0
1
0
1
0
1
0
0
1
0
0
0
0
0
1
1
0
0
0
1
1
1
0
1
0
1
1
1
0
0
1
0
0
Таким образом, правильный ответ – 3 .
Решение (комментарий к таблице)
- Исходное выражение истинно только тогда, когда и , то есть только при (в таблице истинности одна единица, остальные – нули)
7) Выражение истинно, если хотя бы одна из переменных равна нулю, то есть, оно будет ложно только при (в таблице истинности один нуль, остальные – единицы).
Решение (комментарий к таблице)
- Аналогично выражение ложно только при , а в остальных случаях – истинно.
- Выражение истинно только при ,а в остальных случаях – ложно.
- Выражение истинно только при
, а в остальных случаях – ложно.
Возможные проблемы Выводы
- Сравнительно большой объем работы.
- Очевидно, что проще использовать первый вариант решения (упрощение исходного выражения и, если нужно, ответов), но для этого нужно помнить формулы.
- Если формулы забыты, всегда есть простой (хотя и более трудоемкий) вариант решения через таблицы истинности.
B 4 (высокий уровень)
Укажите значения переменных К, L, M, N, при которых логическое выражение
(¬(М L) К) → (¬К ¬М) N)
ложно.
Ответ запишите в виде строки из 4 символов: значений переменных К, L, М и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что К=1, L=1, M=0, N=1.
Решение (вариант 1)
- Запишем уравнение
(¬(М L) К) → (¬К ¬М) N) = 0 , используя более простые обозначения операций:
- Из таблицы истинности операции «импликация» следует, что это выражение ложно тогда и только тогда, когда одновременно и
Решение (вариант 1)
- Первое равенство выполняется тогда и только тогда, когда К=1 и . Отсюда следует , что может быть только при
- Таким образом, три переменных мы уже определили: К = 1 , М = 0, L = 0
- Из второго условия, , при К=1 и М=0 получаем N = 0
- Таким образом, правильный ответ для К, L, М и N соответственно – 1000
Возможные проблемы
- Переменные однозначно определяются только для ситуаций «сумма = 0» (все равны 0) и «произведение = 1» (все равны 1), в остальных случаях нужно рассматривать разные варианты.
- Не всегда выражение сразу распадается на 2 (или более) отдельных уравнения, каждое из которых однозначно определяет некоторые переменные.
Решение (вариант 2)
- Запишем уравнение
(¬(М L) К) → (¬К ¬М) N) = 0, используя более простые обозначения операций:
- Заменим импликацию по формуле :
- Раскроем инверсию сложного выражения по формуле де Моргана:
Решение (вариант 2)
- Упростим выражение
- Тогда получим:
- Мы получили уравнение вида «сумма = 0», в нем все слагаемые должны быть равны нулю.
Поэтому сразу находим
- Таким образом, правильный ответ для К, L, М и N соответственно – 1000
Замечание
Этот способ работает всегда и дает более общее решение; в частности, можно легко обнаружить, что уравнение имеет несколько решений (тогда оно не сведется к форме «сумма = 0» или «произведение = 1»).
Нужно помнить правила преобразования логических выражений и хорошо владеть этой техникой.
B 4 (высокий уровень)
Сколько различных решений имеет уравнение
((K L) → (L M N)) = 0
где K, L, M, N – логические переменные?
В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
Решение
- Перепишем уравнение, используя более простые обозначения операций:
((K + L) → (L · M · N)) = 0.
- Из таблицы истинности операции «импликация» следует, что это равенство верно тогда и только тогда, когда одновременно
K + L = 1 и L · M · N = 0.
- Из уравнения следует, что хотя бы одна из переменных, K или L равна 1 или обе вместе; поэтому рассмотрим три случая.
K = 1 и L = 0; K = 1 и L = 1; K = 0 и L = 1.
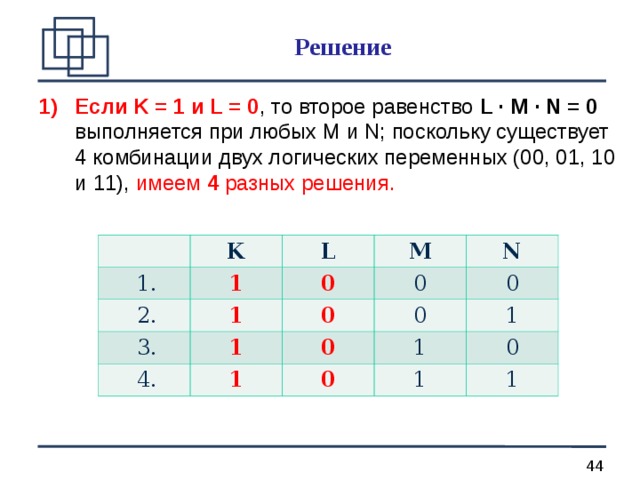
Решение
- Если K = 1 и L = 0 , то второе равенство L · M · N = 0 выполняется при любых М и N; поскольку существует 4 комбинации двух логических переменных (00, 01, 10 и 11), имеем 4 разных решения.
1.
- 1.
K
2.
- 2.
L
1
3.
- 3.
0
1
М
1
N
0
4.
- 4.
0
0
0
0
1
1
1
0
0
1
1
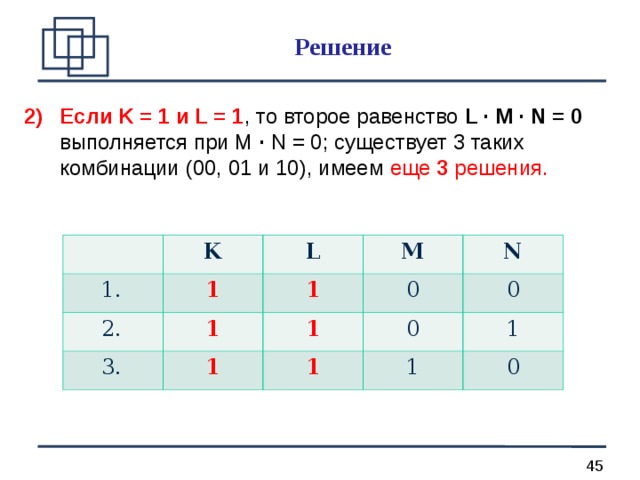
Решение
- Если K = 1 и L = 1 , то второе равенство L · M · N = 0 выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения.
1.
- 1.
K
2.
- 2.
L
1
3.
- 3.
1
М
1
0
N
1
1
0
0
1
1
1
0
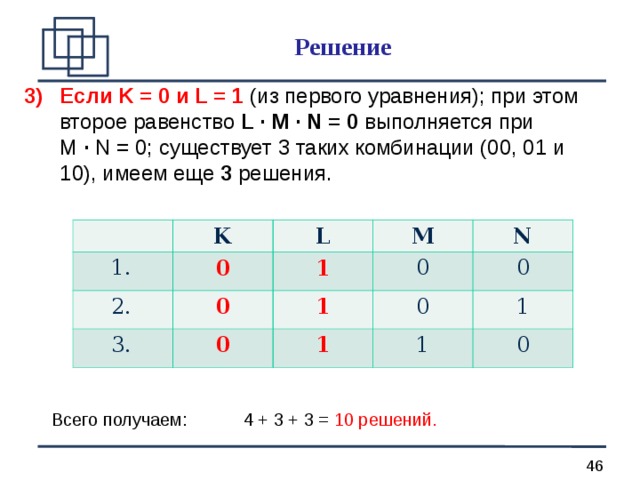
Решение
- Если K = 0 и L = 1 (из первого уравнения); при этом второе равенство L · M · N = 0 выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения.
1.
- 1.
K
2.
- 2.
L
0
3.
- 3.
М
0
1
0
N
0
1
0
0
1
1
1
0
Всего получаем: 4 + 3 + 3 = 10 решений.
Совет
Лучше начинать с того уравнения, где меньше переменных.
Возможные проблемы
Есть риск потерять какие-то решения при переборе вариантов.
ЗАКОНЫ ЛОГИКИ Задание А 7. Вариант 1
Логическое выражение ¬ Y ¬ ((X Y ) ^ ¬ Y) ^X ^ ¬ Y максимально упрощается до выражения:
1) X ^ Y 2) ¬ Y 3) X 4) 1
¬ Y ¬ ( (X Y ) ^ ¬ Y ) ^X ^ ¬ Y =
¬ Y ¬ ( X ^¬ Y Y ^¬ Y ) ^X ^ ¬ Y =
¬ Y ¬ ( X ^¬ Y 0 ) ^X ^ ¬ Y =
¬ Y ¬ (X ^¬ Y) ^X ^ ¬ Y =
¬ Y (¬ X ¬ ¬Y) ^X ^ ¬ Y =
¬ Y (¬ X Y) ^X ^ ¬ Y =
¬ Y (¬ X Y) ^X ^ ¬ Y =
¬ Y (¬ X ^X ^ ¬ Y Y ^X ^ ¬ Y) =
¬ Y (0^ ¬ Y X ^ 0) =
¬ Y 0 = ¬ Y
Правильный ответ – 2
ЗАКОНЫ ЛОГИКИ Задание А 7. Вариант 2
Логическое выражение ¬ (X Y ) ¬X ^ Y X Y максимально упрощается до выражения:
1) 0 2) 1 3) X 4) ¬ X ^ Y
¬ (X Y ) ¬X ^ Y X Y =
¬ X ^ ¬ Y ¬X ^ Y X Y =
¬ X ^ ¬ Y ¬X ^ Y X Y =
¬ X ^ ( ¬ Y Y) X Y =
¬ X ^ 1 X Y =
¬ X X Y =
¬ X X Y =
1 Y =
1 Y = 1
Правильный ответ – 2
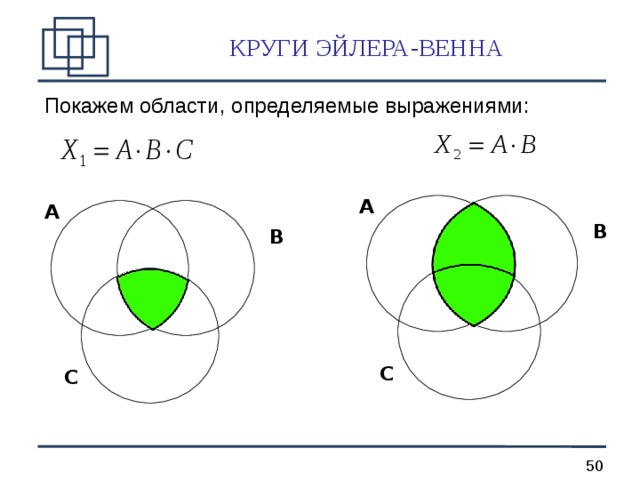
КРУГИ ЭЙЛЕРА-ВЕННА
Покажем области, определяемые выражениями:
A
A
B
B
С
С
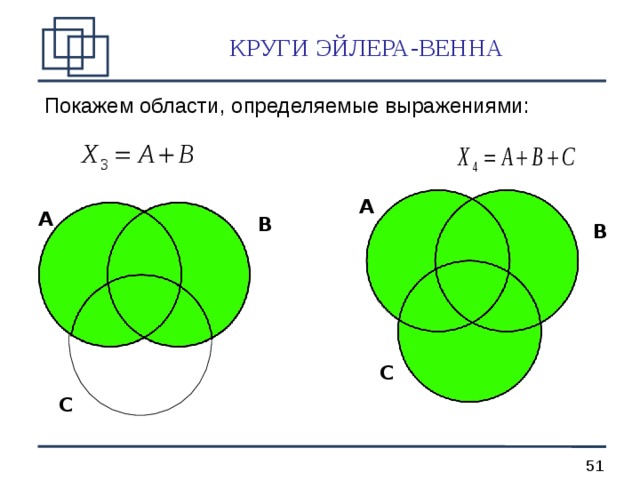
КРУГИ ЭЙЛЕРА-ВЕННА
Покажем области, определяемые выражениями:
A
A
B
B
С
C
51
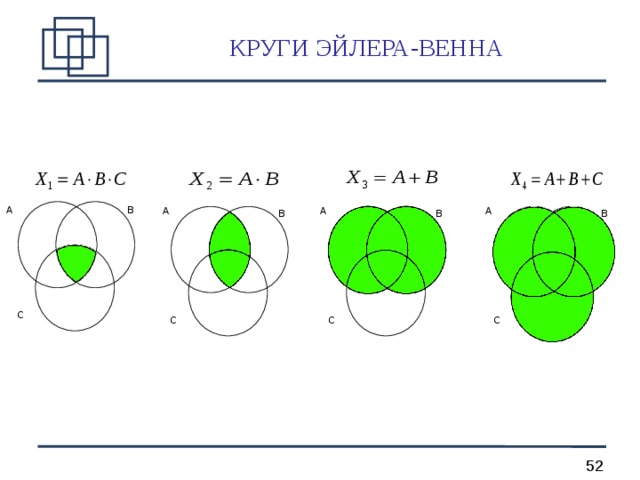
КРУГИ ЭЙЛЕРА-ВЕННА
A
B
A
A
A
B
B
B
С
С
С
С
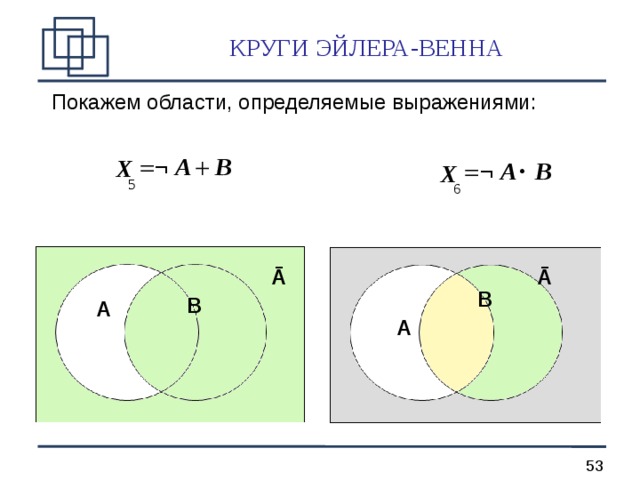
КРУГИ ЭЙЛЕРА-ВЕННА
Покажем области, определяемые выражениями:
B
¬ A
X
B
¬ A
∙
X
5
6
Ā
Ā
Ā
Ā
B
A
A
B
B
B
A
A
53
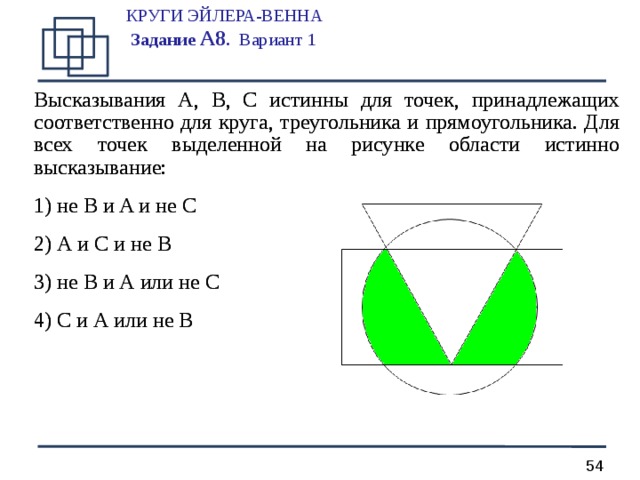
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 1
Высказывания A, B, C истинны для точек, принадлежащих соответственно для круга, треугольника и прямоугольника. Для всех точек выделенной на рисунке области истинно высказывание:
Высказывания A, B, C истинны для точек, принадлежащих соответственно для круга, треугольника и прямоугольника. Для всех точек выделенной на рисунке области истинно высказывание:
- не B и A и не C
- A и C и не B
- не B и A или не C
- C и A или не B
- не B и A и не C
- A и C и не B
- не B и A или не C
- C и A или не B
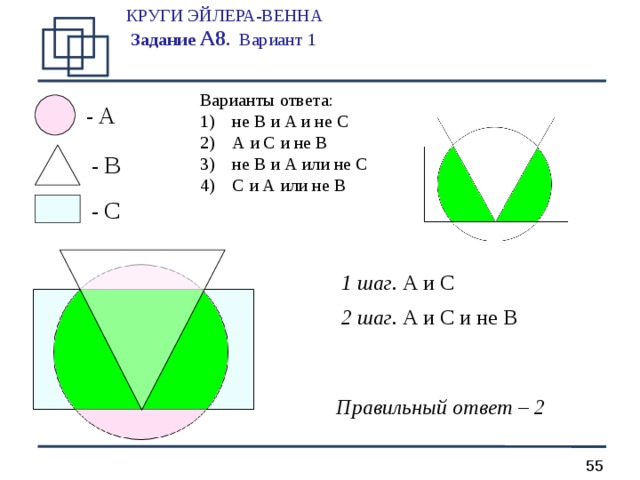
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 1
Варианты ответа:
- не B и A и не C
- A и C и не B
- не B и A или не C
- C и A или не B
- A
- B
- C
1 шаг. A и C
2 шаг. A и C и не B
Правильный ответ – 2
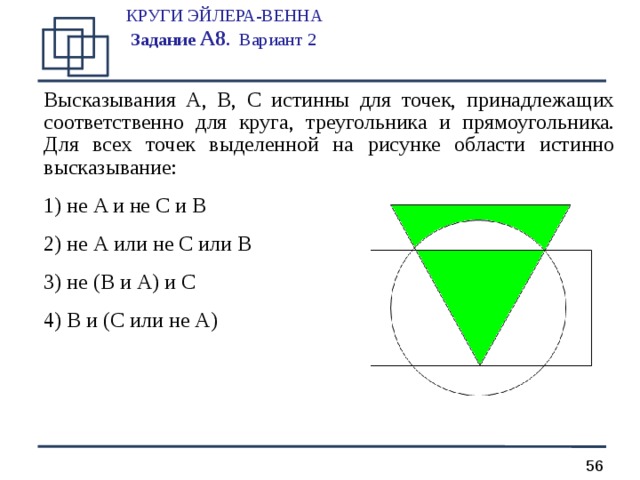
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 2
Высказывания A, B, C истинны для точек, принадлежащих соответственно для круга, треугольника и прямоугольника. Для всех точек выделенной на рисунке области истинно высказывание:
- не A и не C и B
- не A или не C или B
- не ( B и A ) и C
- B и ( C или не A )
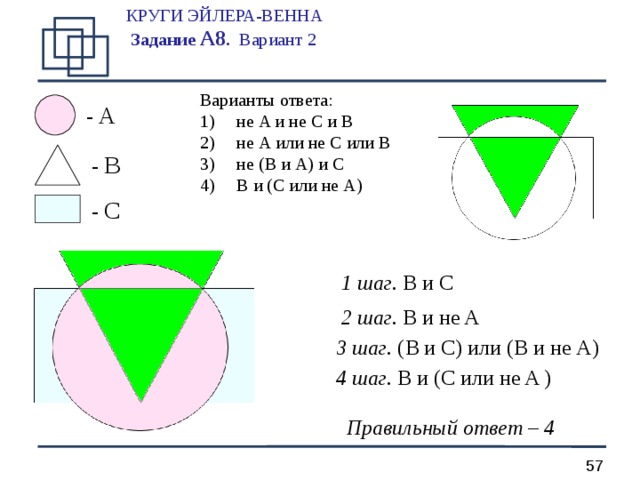
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 2
Варианты ответа:
- не A и не C и B
- не A или не C или B
- не ( B и A ) и C
- B и ( C или не A )
- A
- B
- C
1 шаг. B и C
2 шаг. B и не A
3 шаг. ( B и C ) или ( B и не A )
4 шаг. B и ( C или не A )
Правильный ответ – 4
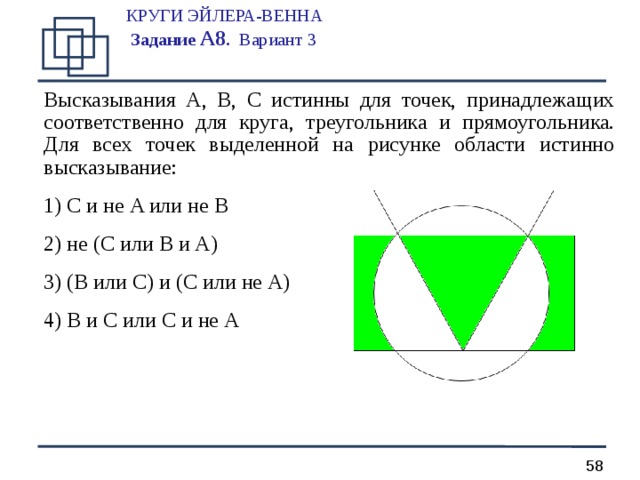
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 3
Высказывания A, B, C истинны для точек, принадлежащих соответственно для круга, треугольника и прямоугольника. Для всех точек выделенной на рисунке области истинно высказывание:
- C и не A или не B
- не ( C или B и A )
- ( B или C ) и ( C или не A )
- B и C или C и не A
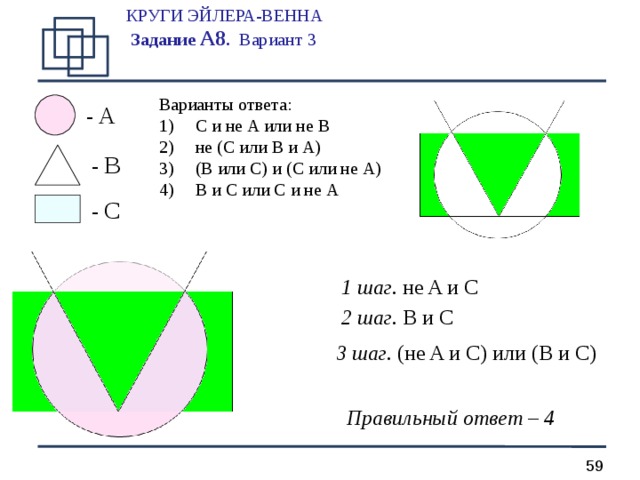
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 3
Варианты ответа:
- C и не A или не B
- не ( C или B и A )
- ( B или C ) и ( C или не A )
- B и C или C и не A
- A
- B
- C
1 шаг. не A и C
2 шаг. B и C
3 шаг. (не A и C ) или ( B и С)
Правильный ответ – 4
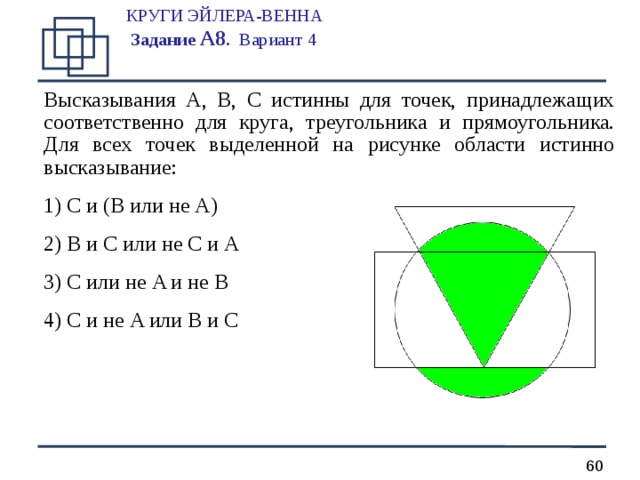
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 4
Высказывания A, B, C истинны для точек, принадлежащих соответственно для круга, треугольника и прямоугольника. Для всех точек выделенной на рисунке области истинно высказывание:
- C и ( B или не A )
- B и C или не C и A
- C или не A и не B
- C и не A или B и C
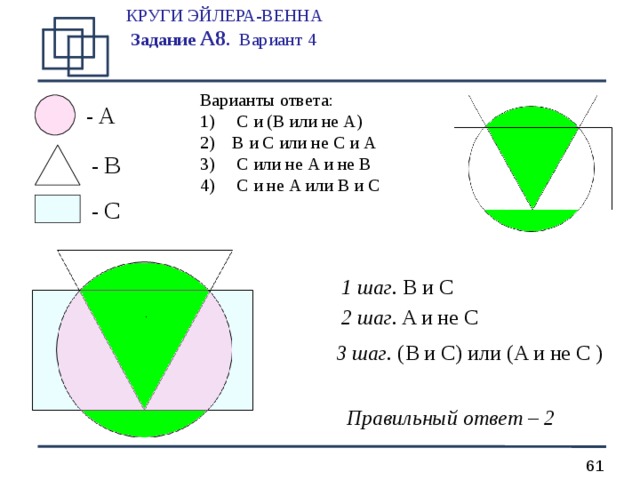
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 4
Варианты ответа:
- C и ( B или не A )
- B и C или не C и A
- C или не A и не B
- C и не A или B и C
- A
- B
- C
1 шаг. B и C
2 шаг. A и не C
3 шаг. ( B и C ) или ( A и не C )
Правильный ответ – 2
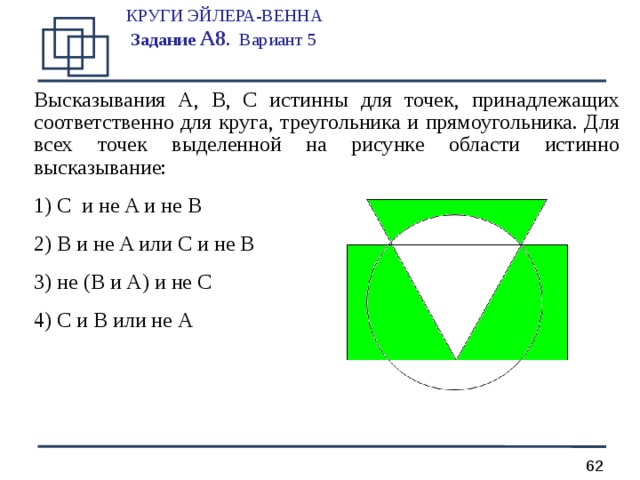
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 5
Высказывания A, B, C истинны для точек, принадлежащих соответственно для круга, треугольника и прямоугольника. Для всех точек выделенной на рисунке области истинно высказывание:
- C и не A и не B
- B и не A или C и не B
- не ( B и A ) и не C
- C и B или не A
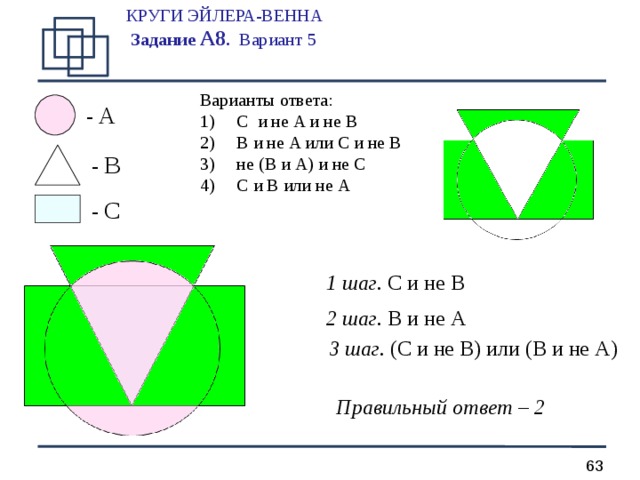
КРУГИ ЭЙЛЕРА-ВЕННА Задание А 8 . Вариант 5
Варианты ответа:
- C и не A и не B
- B и не A или C и не B
- не ( B и A ) и не C
- C и B или не A
- A
- B
- C
1 шаг. C и не B
2 шаг. B и не A
3 шаг. ( C и не B ) или ( B и не A )
Правильный ответ – 2
B 10 (повышенный уровень, время – 5 мин)
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ | , а для логической операции «И» – &.
1) принтеры & сканеры & продажа
2) принтеры & продажа
3) принтеры | продажа
4) принтеры | сканеры | продажа
Решение (вариант 1)
1) принтеры & сканеры & продажа
2) принтеры & продажа
3) принтеры | продажа
4) принтеры | сканеры | продажа
- Меньше всего результатов выдаст запрос с наибольшими ограничениями – первый (нужны одновременно принтеры, сканеры и продажа).
- На втором месте – второй запрос (одновременно принтеры и сканеры).
- Далее – третий запрос (принтеры или сканеры).
- Четвертый запрос дает наибольшее количество результатов (принтеры или сканеры или продажа).
Таким образом, верный ответ – 1234 .
Возможные проблемы
- Нужно внимательно читать условие, так как в некоторых задачах требуется перечислить запросы в порядке убывания количества результатов, а в некоторых – в порядке возрастания.
- Можно ошибиться в непривычных значках: «И» = &, «ИЛИ» = |.
- Можно перепутать значение операций «И» и «ИЛИ», а также порядок выполнения цепочки операций (сначала – «И», потом – «ИЛИ»).
- Для сложных запросов не всегда удается так просто расположить запросы по возрастанию (или убыванию) ограничений.
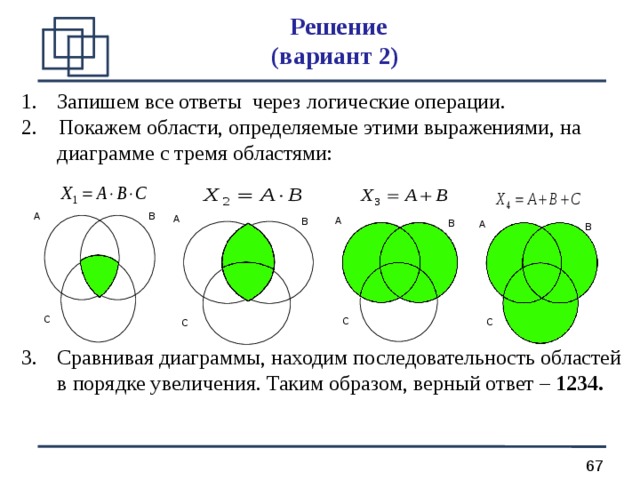
Решение (вариант 2)
- Запишем все ответы через логические операции.
2. Покажем области, определяемые этими выражениями, на диаграмме с тремя областями:
- Сравнивая диаграммы, находим последовательность областей в порядке увеличения. Таким образом, верный ответ – 1234.
A
B
A
A
B
B
A
B
С
С
С
С
Возможные проблемы
- Получается громоздкий рисунок, если используется более трех переменных (более трех кругов).
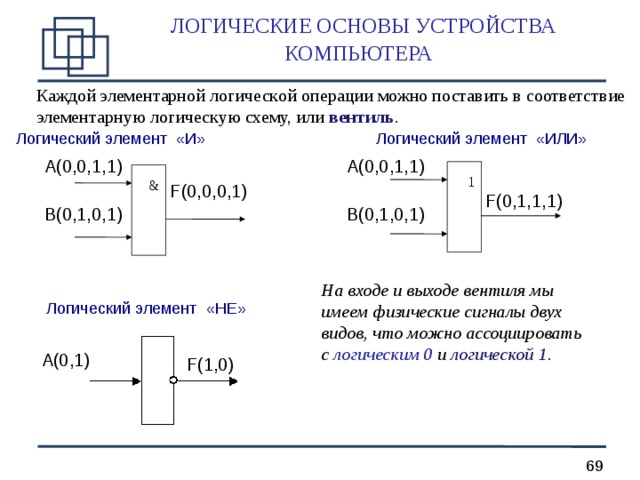
ЛОГИЧЕСКИЕ ОСНОВЫ УСТРОЙСТВА КОМПЬЮТЕРА
Каждой элементарной логическ ой операции можно поставить в соответствие элементарную логическ ую схему, или вентиль .
Логический элемент «И»
Логический элемент «ИЛИ»
А(0,0,1,1)
А(0,0,1,1)
1
&
F(0,0,0,1)
F(0,1,1,1)
B(0,1,0,1)
B(0,1,0,1)
На входе и выходе вентиля мы имеем физические сигналы двух видов, что можно ассоциировать с логическим 0 и логическ ой 1 .
Логический элемент «НЕ»
А(0,1)
F(1,0)
69
ЛОГИЧЕСКИЕ СХЕМЫ
Построение логических схем по булеву выражению.
- Определить число переменных.
- Определить количество логических операций и их порядок.
- Построить для каждой логической операции свою схему (если это возможно).
- Объединить логические схеме в порядке выполнения логических операций.
Построение булева выражения по логической схеме.
- На выходе каждого логического элемента записать результат логической операции.
- Записать получившуюся формулу на выходе последнего элемента.
- Упростить получившуюся формулу.
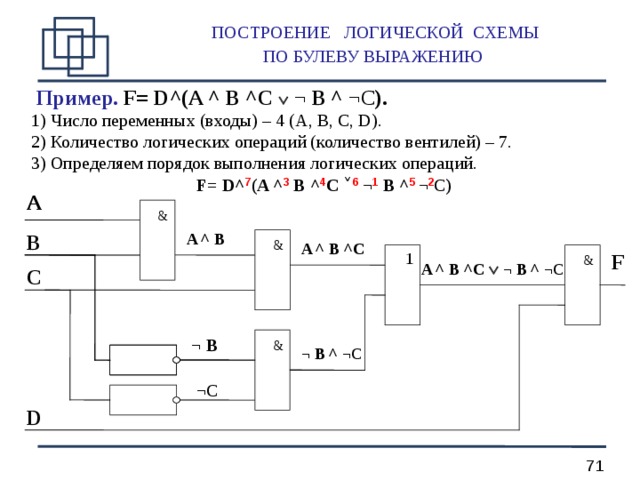
ПОСТРОЕНИЕ ЛОГИЧЕСКОЙ СХЕМЫ ПО БУЛЕВУ ВЫРАЖЕНИЮ
Пример. F= D ^(A ^ B ^C ¬ B ^ ¬C ).
- Число переменных (входы) – 4 ( A, B, C, D) .
- Количество логических операций (количество вентилей) – 7.
- Определяем порядок выполнения логических операций.
F= D ^ 7 (A ^ 3 B ^ 4 C ˅ 6 ¬ 1 B ^ 5 ¬ 2 C )
A
A
&
B
A ^ B
&
A ^ B ^C
&
F
1
A ^ B ^C ¬ B ^ ¬C
C
&
¬ B
¬ B ^ ¬C
¬C
D
71
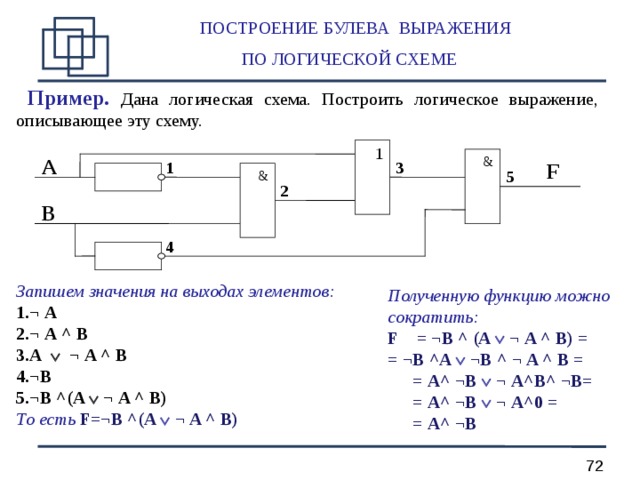
ПОСТРОЕНИЕ БУЛЕВА ВЫРАЖЕНИЯ ПО ЛОГИЧЕСКОЙ СХЕМЕ
Пример. Дана логическая схема. Построить логическое выражение, описывающее эту схему.
Запишем значения на выходах элементов:
- ¬ A
- ¬ A ^ B
- A ¬ A ^ B
- ¬B
- ¬B ^( A ¬ A ^ B )
То есть F=¬B ^( A ¬ A ^ B )
1
&
A
3
1
F
5
&
2
B
4
Полученную функцию можно сократить:
F = ¬B ^ ( A ¬ A ^ B ) = = ¬B ^ A ¬B ^ ¬ A ^ B =
= A ^ ¬B ¬ A^ B ^ ¬B=
= A ^ ¬B ¬ A^ 0 =
= A ^ ¬B
ПОСТРОЕНИЕ БУЛЕВА ВЫРАЖЕНИЯ ПО ТАБЛИЦЕ ИСТИННОСТИ
- Для каждой строки таблицы с единичным значением функции построить минтерм . (Минтермом называется терм-произведение, в котором каждая переменная встречается только один раз – либо с отрицанием, либо без него). Переменные, имеющие нулевые значения в строке, входят в минтерм с отрицанием , а переменные со значением 1 – без отрицания ).
- Объединить все минтермы операцией дизьюнкция , что даст стандартную сумму произведений для заданной таблицы истинности.
ПОСТРОЕНИЕ БУЛЕВА ВЫРАЖЕНИЯ ПО ТАБЛИЦЕ ИСТИННОСТИ
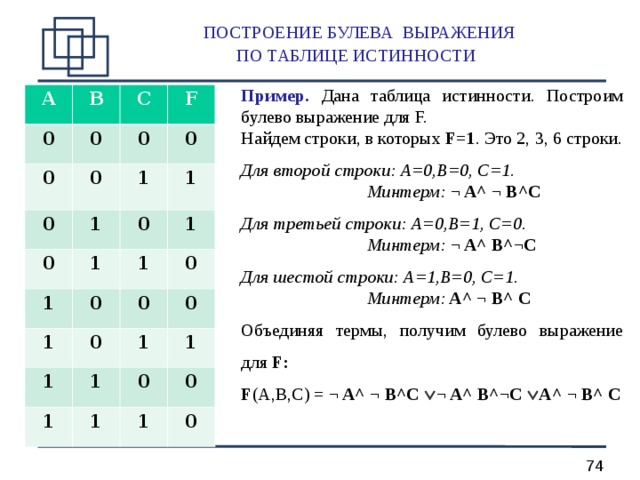
Пример. Дана таблица истинности. Построим булево выражение для F.
Найдем строки, в которых F=1 . Это 2, 3, 6 строки.
Для второй строки: A=0,B=0, C=1.
Минтерм: ¬ A^ ¬ B^C
Для третьей строки: A=0,B= 1 , C= 0 .
Минтерм: ¬ A^ B^¬C
Для шестой строки: A= 1 ,B=0, C= 1 .
Минтерм: A^ ¬ B^ C
Объединяя термы, получим булево выражение для F :
F (A,B,C) = ¬ A^ ¬ B^C ¬ A^ B^¬C A^ ¬ B^ C
A
0
B
0
0
C
F
0
0
0
0
1
1
0
1
1
0
1
0
1
1
1
0
0
1
0
0
1
1
1
1
0
1
0
1
0
A11 Вариант 2008_04_30
Дана таблица истинности выражения F.
Какое выражение соответствует F ?
- ¬X ^ Y^Z X ^ ¬ Y ^Z X ^ Y ^ ¬ Z
- X ^ Y^Z X ^ ¬ Y ^Z X ^ ¬ Y ^ ¬ Z
- ¬X ^ Y^Z X ^ Y ^Z X ^ ¬ Y ^ Z
- ¬X ^ ¬ Y^ ¬ Z ¬ X ^ Y ^Z X ^ Y ^ ¬ Z
Построим булево выражение для данной таблицы истинности:
Найдем строки, в которых F=1 . Это 1, 4, 7 строки.
Для первой строки минтерм:
¬X ^ ¬ Y^ ¬ Z
Для четвертой строки минтерм:
¬ X ^ Y ^Z
Для седьмой строки минтерм:
X ^ Y ^ ¬ Z
Объединяя термы, получим булево выражение для F :
F = ¬X ^ ¬ Y^ ¬ Z ¬ X ^ Y ^Z X ^ Y ^ ¬ Z
Таким образом, правильный ответ: 4
X
0
Y
0
0
Z
F
0
0
0
0
1
1
1
1
1
0
0
0
1
0
1
1
0
0
1
0
1
1
1
1
0
0
1
1
0
A 9 (базовый уровень, время – 2 мин)
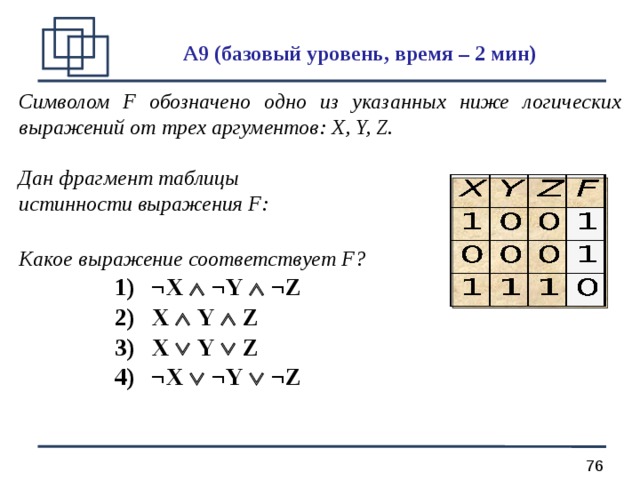
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
- ¬X ¬Y ¬Z X Y Z X Y Z ¬X ¬Y ¬Z
- ¬X ¬Y ¬Z X Y Z X Y Z ¬X ¬Y ¬Z
- ¬X ¬Y ¬Z X Y Z X Y Z ¬X ¬Y ¬Z
- ¬X ¬Y ¬Z
- X Y Z
- X Y Z
- ¬X ¬Y ¬Z
Решение (О сновной вариант )
- Нужно для каждой строчки подставить заданные значения X, Y и Z во все функции, заданные в ответах, и сравнить результаты с соответствующими значениями F для этих данных.
- Если для какой-нибудь комбинации X, Y и Z результат не совпадает с соответствующим значением F , оставшиеся строчки можно не рассматривать, поскольку для правильного ответа все три результата должны совпасть со значениями функции F.
Решение (О сновной вариант )
- Перепишем ответы в других обозначениях:
- ¬X ¬Y ¬Z =
- ¬X ¬Y ¬Z =
- ¬X ¬Y ¬Z =
- ¬X ¬Y ¬Z =
- X Y Z =
- X Y Z =
- X Y Z =
- X Y Z =
- X Y Z =
- X Y Z =
- X Y Z =
- X Y Z =
- ¬X ¬Y ¬Z =
- ¬X ¬Y ¬Z =
- ¬X ¬Y ¬Z =
- ¬X ¬Y ¬Z =
Решение (О сновной вариант )
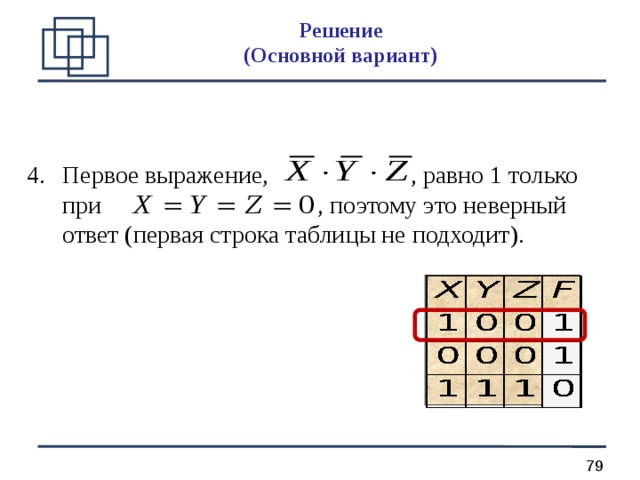
- Первое выражение, , равно 1 только при , поэтому это неверный ответ (первая строка таблицы не подходит).
Решение (О сновной вариант )
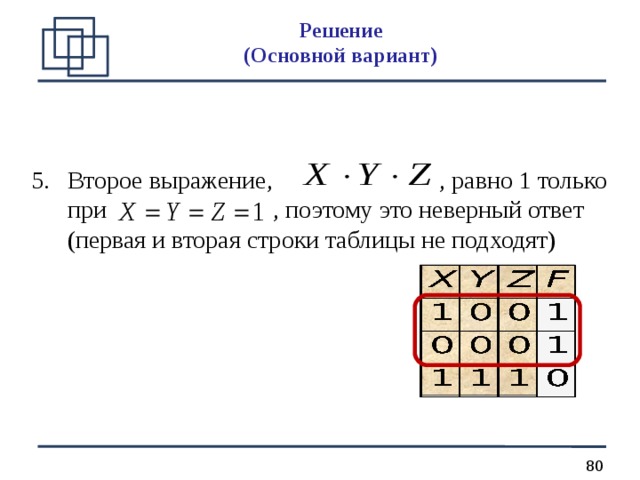
- Второе выражение, , равно 1 только при , поэтому это неверный ответ (первая и вторая строки таблицы не подходят)
Решение (О сновной вариант )
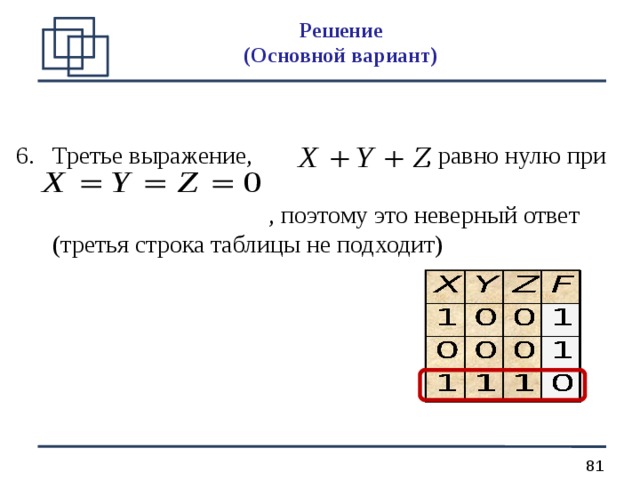
- Третье выражение, , равно нулю при , поэтому это неверный ответ (третья строка таблицы не подходит)
Решение (О сновной вариант )
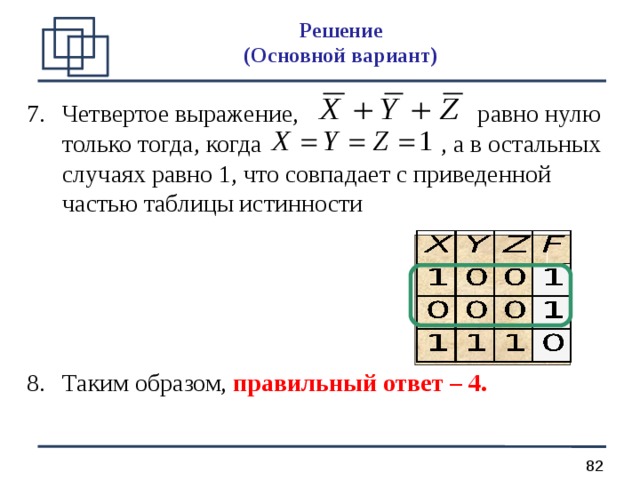
- Четвертое выражение, равно нулю только тогда, когда , а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности
- Таким образом, правильный ответ – 4.
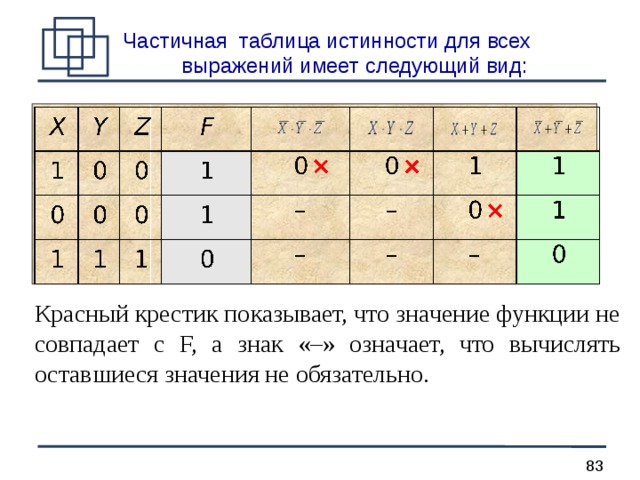
Частичная таблица истинности для всех выражений имеет следующий вид:
Красный крестик показывает, что значение функции не совпадает с F, а знак «–» означает, что вычислять оставшиеся значения не обязательно.
Возможные ловушки и проблемы
- Серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений, поэтому рекомендуется сначала внимательно перевести их в удобный вид.
- Расчет на то, что ученик перепутает значки и .
- В некоторых случаях заданные выражения-ответы лучше сначала упростить, особенно если они содержат импликацию или инверсию сложных выражений.
Решение ( вариант 2)
- Часто правильный ответ – это самая простая функция, удовлетворяющая частичной таблице истинности, то есть, имеющая единственный нуль или единственную единицу в полной таблице истинности.
- В этом случае можно найти такую функцию и проверить, есть ли она среди данных ответов.
- В приведенной задаче в столбце F есть единственный нуль для комбинации .
- Выражение, которое имеет единственный нуль для этой комбинации, это , оно есть среди приведенных ответов ( ответ 4 ).
A 9 (базовый уровень, время – 2 мин)
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) ¬X ¬Y ¬Z
2) X Y Z
3) X ¬Y ¬Z
4) X ¬Y ¬Z
Решение
- Перепишем ответы в других обозначениях:
- ¬X ¬Y ¬Z = X Y Z = X ¬Y ¬Z = X ¬Y ¬Z =
- ¬X ¬Y ¬Z =
- X Y Z =
- X ¬Y ¬Z =
- X ¬Y ¬Z =
- В столбце F есть единственная единица для комбинации , простейшая функция, истинная (только) для этого случая, имеет вид , она есть среди приведенных ответов.
- Таким образом, правильный ответ – 3.
=2000 », равно: 1) 8 2) 6 3) 3 4) 14 Запрос Год издания = 2000 или возраст средний N Неверно, что (возраст = средний или возраст = младший) 25 9 Год издания младший 14 " width="640"
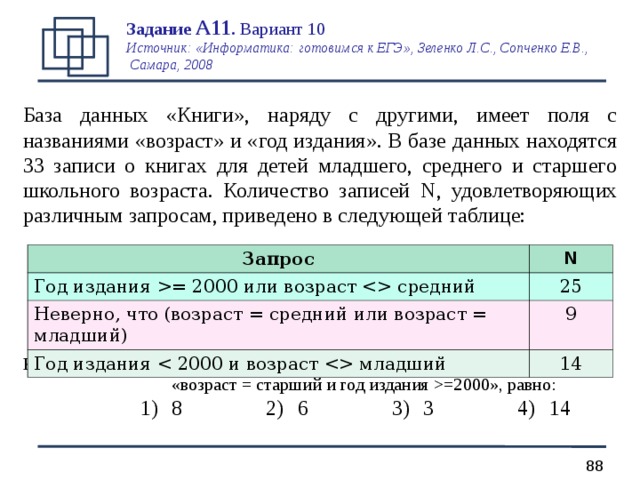
Задание А11 . Вариант 10 Источник: «Информатика: готовимся к ЕГЭ», Зеленко Л.С., Сопченко Е.В., Самара, 2008
База данных «Книги», наряду с другими, имеет поля с названиями «возраст» и «год издания». В базе данных находятся 33 записи о книгах для детей младшего, среднего и старшего школьного возраста. Количество записей N , удовлетворяющих различным запросам, приведено в следующей таблице:
Количество записей, удовлетворяющих запросу «возраст = старший и год издания =2000 », равно:
1) 8 2) 6 3) 3 4) 14
Запрос
Год издания = 2000 или возраст средний
N
Неверно, что (возраст = средний или возраст = младший)
25
9
Год издания младший
14
=2000 2 шаг. По закону де Моргана преобразуем вторую строку: НЕ (СРЕД или МЛ) = НЕ СРЕД и НЕ МЛ =9, следовательно старших (СТ) = 9 Запрос N Год издания = 2000 или возраст средний 25 Неверно, что (возраст = средний или возраст = младший) 9 Год издания 2000 и возраст младший 14 НЕ (возраст = средний или возраст = младший) НЕ (возраст = средний) и НЕ (возраст = младший) 9 возраст = старший 9 9 " width="640"
Задание А 11 . Вариант 10 Источник: «Информатика: готовимся к ЕГЭ», Зеленко Л.С., Сопченко Е.В.,
Самара, 2008
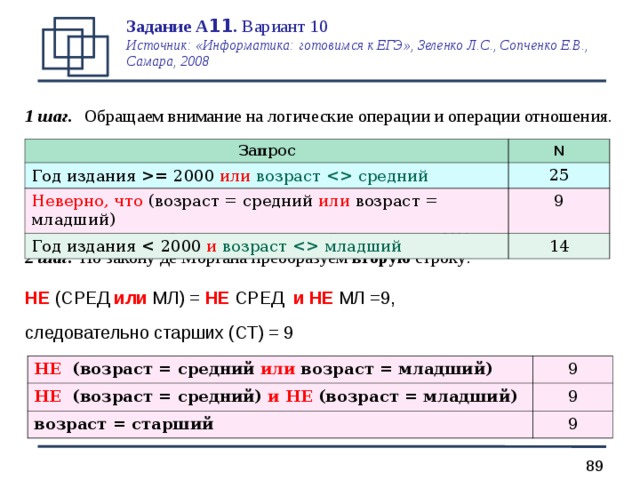
1 шаг. Обращаем внимание на логические операции и операции отношения.
Запрос «возраст = старший и год издания =2000
2 шаг. По закону де Моргана преобразуем вторую строку:
НЕ (СРЕД или МЛ) = НЕ СРЕД и НЕ МЛ =9,
следовательно старших (СТ) = 9
Запрос
N
Год издания = 2000 или возраст средний
25
Неверно, что (возраст = средний или возраст = младший)
9
Год издания 2000 и возраст младший
14
НЕ (возраст = средний или возраст = младший)
НЕ (возраст = средний) и НЕ (возраст = младший)
9
возраст = старший
9
9
=2000 3 шаг. По законам де Моргана и двойного отрицания преобразуем первую строку: Запрос N Год издания = 2000 или возраст средний 25 возраст = старший 9 Год издания 2000 и возраст младший 14 Год издания = 2000 или возраст средний НЕ (Год издания = 2000 или (возраст средний)) 25 НЕ (Год издания = 2000 ) и НЕ (возраст средний) 33-25=8 8 Год издания и возраст = средний 8 " width="640"
Задание А 11 . Вариант 10 Источник: «Информатика: готовимся к ЕГЭ», Зеленко Л.С., Сопченко Е.В.,
Самара, 2008
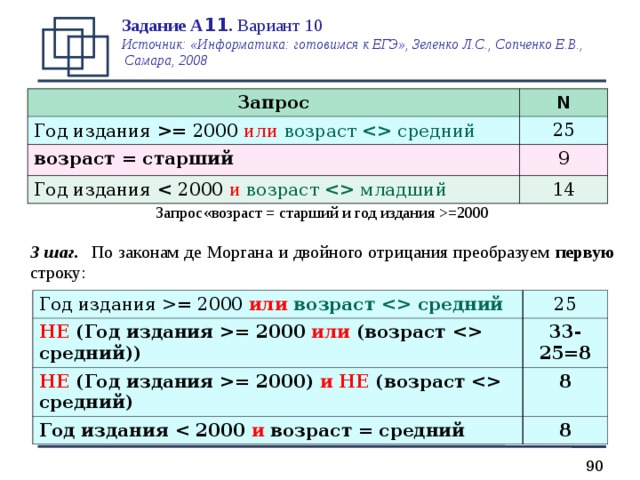
Запрос «возраст = старший и год издания =2000
3 шаг. По законам де Моргана и двойного отрицания преобразуем первую строку:
Запрос
N
Год издания = 2000 или возраст средний
25
возраст = старший
9
Год издания 2000 и возраст младший
14
Год издания = 2000 или возраст средний
НЕ (Год издания = 2000 или (возраст средний))
25
НЕ (Год издания = 2000 ) и НЕ (возраст средний)
33-25=8
8
Год издания и возраст = средний
8
=2000 » 4 шаг. Запрос возраст младший соответствует запросу возраст = старший или возраст = средний . Преобразуем третью строку: Запрос N Год издания и возраст = средний 8 возраст = старший 9 Год издания 2000 и возраст младший 14 Год издания и возраст младший Год издания и ( возраст = старший и ли возраст = средний ) 14 14 " width="640"
Задание А 11 . Вариант 10 Источник: «Информатика: готовимся к ЕГЭ», Зеленко Л.С., Сопченко Е.В.,
Самара, 2008
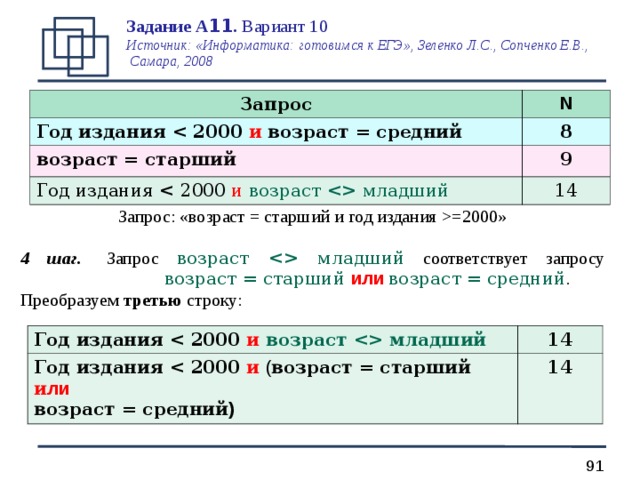
Запрос: «возраст = старший и год издания =2000 »
4 шаг. Запрос возраст младший соответствует запросу возраст = старший или возраст = средний .
Преобразуем третью строку:
Запрос
N
Год издания и возраст = средний
8
возраст = старший
9
Год издания 2000 и возраст младший
14
Год издания и возраст младший
Год издания и ( возраст = старший и ли возраст = средний )
14
14
=2000 » Варианты ответа: 1) 8 2) 6 3) 3 4) 14 5 шаг. Сравнивая первую и третью строки, делаем вывод, что 6 шаг. Из второй строки известно сколько всего возраст = старший (9). Делаем вывод, что Правильный ответ: 3 Запрос N Год издания и возраст = средний 8 возраст = старший 9 Год издания и ( возраст = старший и ли возраст = средний ) 14 Год издания и возраст = старший 14-8=6 Год издания = 2000 и возраст = старший 9-6=3 " width="640"
Задание А 11 . Вариант 10 Источник: «Информатика: готовимся к ЕГЭ», Зеленко Л.С., Сопченко Е.В.,
Самара, 2008
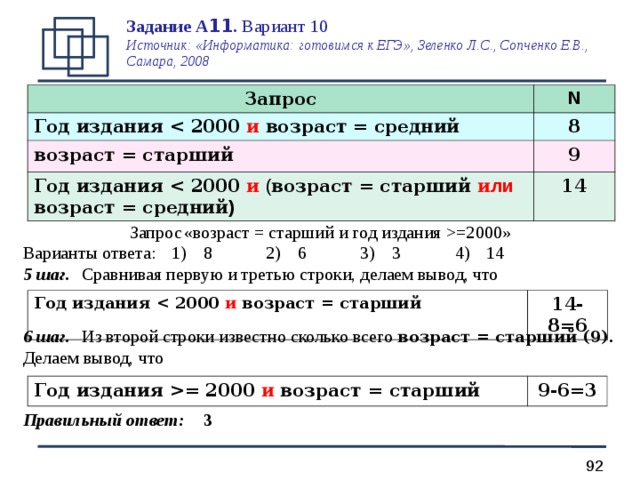
Запрос «возраст = старший и год издания =2000 »
Варианты ответа: 1) 8 2) 6 3) 3 4) 14
5 шаг. Сравнивая первую и третью строки, делаем вывод, что
6 шаг. Из второй строки известно сколько всего возраст = старший (9).
Делаем вывод, что
Правильный ответ: 3
Запрос
N
Год издания и возраст = средний
8
возраст = старший
9
Год издания и ( возраст = старший и ли возраст = средний )
14
Год издания и возраст = старший
14-8=6
Год издания = 2000 и возраст = старший
9-6=3
Алгоритм решения логических задач
- внимательно изучить условие;
- выделить простые высказывания и обозначить их латинскими буквами;
- записать условие задачи на языке алгебры логики;
- составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения, приравнять произведение единице;
- упростить формулу, проанализировать полученный результат или составить таблицу истинности, найти по таблице значения переменных, для которых Р = 1, проанализировать результаты.
B 6 (повышенный уровень, время – 8 мин) Пример 1 (2007)
В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.
Один считает, что первой будет Наташа, а Маша будет второй .
Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место .
Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй .
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов . Какое место на чемпионате заняли Наташа, Маша, Люда, Рита ?
(В ответе перечислите подряд без пробелов числа, соответствующие местам девочек в указанном порядке имен.)
В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.
Один считает, что первой будет Наташа, а Маша будет второй.
Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место.
Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.
Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?
(В ответе перечислите подряд без пробелов числа, соответствующие местам девочек в указанном порядке имен.)
B 6 (повышенный уровень, время – 8 мин) Пример 1 (2007)
Н1 М2 v Н1 М2 =1
Л2 Р4 v Л2 Р4 =1
Р3 Н2 v Р3 Н2 =1
- Н1 М2
- Л2 Р4
- Р3 Н2
(Н1 М2 v Н1 М2) (Л2 Р4 v Л2 Р4 ) (Р3 Н2 v Р3 Н2 ) =
(Н1 • М2 + Н1•М2) •
(Л2•Р4•Р3•Н2 +Л2• Р4 • Р3 •Н2 + Л2•Р4•Р3•Н2 + Л2•Р4•Р3•Н2) =
Н1• М2 •Л2•Р4•Р3• Н2 + Н1• М2 • Л2 •Р4•Р3• Н2 + Н1• М2 • Л2 •Р4•Р3•Н2 +
Н1 •М2•Л2•Р4•Р3• Н2 + Н1•М2• Л2 •Р4•Р3• Н2 + Н1•М2•Л2•Р4•Р3•Н2 =
= Н1•М2•Л2•Р4•Р3•Н2
Наташа – 1
Маша – 4
Люда – 2
Рита – 3
Ответ: 1423
B 6 (повышенный уровень, время – 8 мин) Пример 2 (200 8 )
Перед началом Турнира Четырех болельщики высказали следующие предположения по поводу своих кумиров:
А) Макс победит, Билл – второй;
В) Билл – третий, Ник – первый;
С) Макс – последний, а первый – Джон.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на турнире заняли Джон, Ник, Билл, Макс? (В ответе перечислите подряд без пробелов места участников в указанном порядке имен.)
Решение
Применим к этой задаче формальный аппарат математической логики.
Каждый из трех болельщиков высказал два утверждения, всего получилось 6; обозначим их так:
- Применим к этой задаче формальный аппарат математической логики. Каждый из трех болельщиков высказал два утверждения, всего получилось 6; обозначим их так:
A : М1 = «Макс – первый», Б2 = «Билл – второй»
B : Н1 = «Ник – первый», Б3 = «Билл – третий»
C : Д1 = «Джон – первый», М4 = «Макс – четвертый»
- A : М1 = «Макс – первый», Б2 = «Билл – второй» B : Н1 = «Ник – первый», Б3 = «Билл – третий» C : Д1 = «Джон – первый», М4 = «Макс – четвертый»
- A : М1 = «Макс – первый», Б2 = «Билл – второй» B : Н1 = «Ник – первый», Б3 = «Билл – третий» C : Д1 = «Джон – первый», М4 = «Макс – четвертый»
Теперь нужно записать, что у каждого одно высказывание верно, а второе неверно:
- Теперь нужно записать, что у каждого одно высказывание верно, а второе неверно:
- М1 Б2
- Б3 Н1
- М4 Д2
М1 Б2 v М1 Б2 =1
Б3 Н1 v Б3 Н1 =1
М4 Д2 v М4 Д2 =1
Ё
Ё
Ё
Ё
Решение
( М1 · ¬ Б2 + ¬ М1 · Б2 ) · (Б3 · ¬ Н1+ ¬ Б3 · Н1) ·(М4 · ¬ Д1+ ¬ М4 · Д1)
=( М1 · ¬ Б2 · Б3 · ¬ Н1 + М1 · ¬ Б2 · ¬ Б3 · Н1 + ¬ М1 · Б2 · Б3 · ¬ Н1 +
+ ¬ М1 · Б2 · ¬ Б3 · Н1) · (М4 · ¬ Д1+ ¬ М4 · Д1) =
=( М1 · ¬ Б2 · Б3 · ¬ Н1 + ¬ М1 · Б2 · ¬ Б3 · Н1) · (М4 · ¬ Д1+ ¬ М4 · Д1)
= М1 · ¬ Б2 · Б3 · ¬ Н1 · М4 · ¬ Д1+ М1 · ¬ Б2 · Б3 · ¬ Н1 · ¬ М4 · Д1 +
+ ¬ М1 · Б2 · ¬ Б3 · Н1 · М4 · ¬ Д1+ ¬ М1 · Б2 · ¬ Б3 · Н1 · ¬ М4 · Д1 =
= ¬ М1 · Б2 · ¬ Б3 · Н1 · М4 , следовательно
Ник – первый, Билл – второй, Макс четвертый Джон – третий
- ( М1 · ¬ Б2 + ¬ М1 · Б2 ) · (Б3 · ¬ Н1+ ¬ Б3 · Н1) ·(М4 · ¬ Д1+ ¬ М4 · Д1) =( М1 · ¬ Б2 · Б3 · ¬ Н1 + М1 · ¬ Б2 · ¬ Б3 · Н1 + ¬ М1 · Б2 · Б3 · ¬ Н1 + + ¬ М1 · Б2 · ¬ Б3 · Н1) · (М4 · ¬ Д1+ ¬ М4 · Д1) = =( М1 · ¬ Б2 · Б3 · ¬ Н1 + ¬ М1 · Б2 · ¬ Б3 · Н1) · (М4 · ¬ Д1+ ¬ М4 · Д1) = М1 · ¬ Б2 · Б3 · ¬ Н1 · М4 · ¬ Д1+ М1 · ¬ Б2 · Б3 · ¬ Н1 · ¬ М4 · Д1 + + ¬ М1 · Б2 · ¬ Б3 · Н1 · М4 · ¬ Д1+ ¬ М1 · Б2 · ¬ Б3 · Н1 · ¬ М4 · Д1 = = ¬ М1 · Б2 · ¬ Б3 · Н1 · М4 , следовательно Ник – первый, Билл – второй, Макс четвертый Джон – третий
- ( М1 · ¬ Б2 + ¬ М1 · Б2 ) · (Б3 · ¬ Н1+ ¬ Б3 · Н1) ·(М4 · ¬ Д1+ ¬ М4 · Д1) =( М1 · ¬ Б2 · Б3 · ¬ Н1 + М1 · ¬ Б2 · ¬ Б3 · Н1 + ¬ М1 · Б2 · Б3 · ¬ Н1 + + ¬ М1 · Б2 · ¬ Б3 · Н1) · (М4 · ¬ Д1+ ¬ М4 · Д1) = =( М1 · ¬ Б2 · Б3 · ¬ Н1 + ¬ М1 · Б2 · ¬ Б3 · Н1) · (М4 · ¬ Д1+ ¬ М4 · Д1) = М1 · ¬ Б2 · Б3 · ¬ Н1 · М4 · ¬ Д1+ М1 · ¬ Б2 · Б3 · ¬ Н1 · ¬ М4 · Д1 + + ¬ М1 · Б2 · ¬ Б3 · Н1 · М4 · ¬ Д1+ ¬ М1 · Б2 · ¬ Б3 · Н1 · ¬ М4 · Д1 = = ¬ М1 · Б2 · ¬ Б3 · Н1 · М4 , следовательно Ник – первый, Билл – второй, Макс четвертый Джон – третий
Ответ: 3124
0
0
0
0
0
B 6 (повышенный уровень, время – 8 мин) Пример 3 (2009)
Классный руководитель пожаловался директору, что у него в классе появилась компания из 3-х учеников, один из которых всегда говорит правду, другой всегда лжет, а третий говорит через раз то ложь, то правду. Директор знает, что их зовут Коля, Саша и Миша, но не знает, кто из них правдив, а кто – нет. Однажды все трое прогуляли урок астрономии. Директор знает, что никогда раньше никто из них не прогуливал астрономию. Он вызвал всех троих в кабинет и поговорил с мальчиками. Коля сказал: «Я всегда прогуливаю астрономию. Не верьте тому, что скажет Саша». Саша сказал: «Это был мой первый прогул этого предмета». Миша сказал: «Все, что говорит Коля, – правда». Директор понял, кто из них кто. Расположите первые буквы имен мальчиков в порядке: «говорит всегда правду», «всегда лжет», «говорит правду через раз». (Пример: если бы имена мальчиков были Рома, Толя и Вася, ответ мог бы быть: РТВ).
Решение (вариант 1)
- Во-первых, есть «точная» информация, которая не подвергается сомнению: (*) все трое прогуляли урок астрономии в первый раз.
- Запишем высказывания мальчиков:
Коля: 1. Я всегда прогуливаю астрономию.
2. Саша врет.
Саша: 1. Я в первый раз прогулял астрономию.
Миша: 1. Коля говорит правду.
- Известно, что один из них все время лжет, второй – говорит правду, а третий говорит правду через раз (то есть, из двух его высказываний одно истинно, а второе – ложно).
Решение (вариант 1)
Коля: 1. Я всегда прогуливаю астрономию.
2. Саша врет.
Саша: 1. Я в первый раз прогулял астрономию.
Миша: 1. Коля говорит правду.
- Сопоставив первое высказывание Коли (Я всегда прогуливаю астрономию) и высказывание Саши (Я в первый раз прогулял астрономию) с «точной» информацией (*), сразу определяем, то тут Коля соврал, а Саша сказал правду; это значит, что второе высказывание Коли – тоже неверно, поэтому мальчик Коля всегда лжет.
- Тогда один из оставшихся, Саша или Миша, говорит правду всегда, а второй – через раз.
Решение (вариант 1)
Коля: лжет
Саша: 1. Я в первый раз прогулял астрономию.
Миша: 1. Коля говорит правду.
- Мишино высказывание неверно, поскольку мы уже определили, что Коля лжет; это значит, что Миша не всегда говорит правду, он – « полу-лжец ».
- Тогда получается, что Саша всегда правдив , и действительно, его высказывание верно.
- Таким образом, верный ответ – СКМ (Саша – правдив, Коля – лжец, Миша – «полу-лжец» ).
Возможные проблемы
- Длинное запутанное условие, из которого нужно выделить действительно существенную информацию и формализовать ее.
- Легко по невнимательности перепутать порядок букв в ответе (здесь сначала правдивый, потом – лжец, потом – «полу-лжец»).
B 6 (повышенный уровень, время – 8 мин) Пример 4 (Вариант №2, 2009)
Один из пяти братьев – Никита, Глеб, Игорь, Андрей или Дима – испек маме пирог. Когда она спросила, кто сделал ей такой подарок, братья ответили следующее:
Никита: «Пирог испек Глеб или Игорь».
Глеб: «Это сделал не я и не Дима».
Андрей: «Нет, один из них сказал правду, а другой обманул».
Дима: «Нет, Андрей, ты не прав».
Мама знает, что трое из сыновей всегда говорят правду. Кто же испек пирог?
Решение Пример 4 (Вариант №2, 2009)
Обозначим высказывания:
F = Г+И Никита: «Пирог испек Глеб или Игорь».
K = ¬ Г · ¬ Д Глеб: «Это сделал не я и не Дима».
C = (F · ¬ K) + ( ¬ F · K) Андрей: «Нет, один из них сказал правду, а другой обманул».
W = ¬ C Дима: «Нет, Андрей, ты не прав».
Составим таблицу истинности, найдем в ней строку с тремя истинными высказываниями из F, K, C, W .
По таблице истинности (см. следующий слайд) пирог испек Игорь.
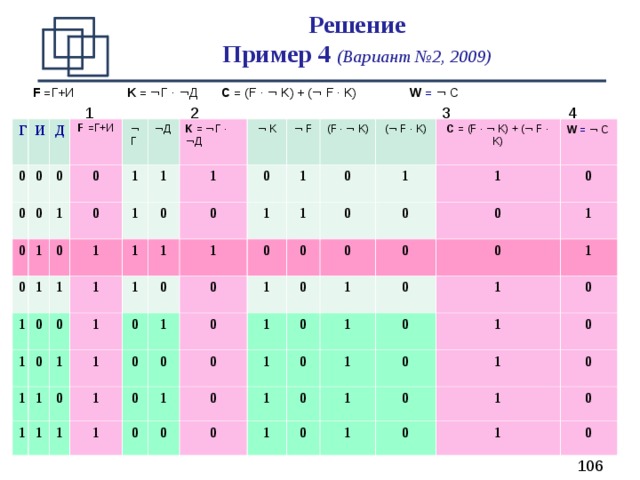
Решение Пример 4 (Вариант №2, 2009)
F = Г+И K = ¬ Г · ¬ Д C = (F · ¬ K) + ( ¬ F · K) W = ¬ C
3
2
1
4
Г
И
0
Д
0
0
0
F = Г+И
0
0
1
0
0
1
¬ Г
1
¬ Д
0
1
0
1
1
1
1
1
0
1
K = ¬ Г · ¬ Д
¬ K
1
0
0
1
1
0
1
1
1
1
¬ F
0
1
1
0
1
1
(F · ¬ K)
1
0
1
1
1
0
0
1
0
0
( ¬ F · K)
0
0
1
1
1
0
1
C = (F · ¬ K) + ( ¬ F · K)
0
1
0
1
0
0
1
1
0
0
0
0
W = ¬ C
1
0
1
1
0
0
0
0
0
0
1
0
1
1
0
0
0
1
1
0
1
1
0
0
1
1
0
0
1
0
0
1
1
0
0
0
1
0
B 6 (повышенный уровень, время – 8 мин) Пример 5 (Вариант №1, 2009)
Три друга – Петр, Роман и Сергей – учатся на математическом (М), физическом (Ф) и химическом (Х) факультетах.
Если Петр математик, то Сергей не физик. Если Роман не физик, то Петр – математик. Если Сергей не математик, то Роман – химик.
Определите специальность каждого. Ответ запишите в виде строки из трех символов, соответствующих первым буквам названия специальностей Петра, Романа и Сергея (в указанном порядке). Так, например, строка МФК соответствует тому, что Петр – математик, Роман – физик, Сергей – химик.
Решение Пример 5 (Вариант №1, 2009)
A Петр - математик
B Сергей - не физик
C Роман физик
D Сергей математик D= = ¬B
E Роман химик E= ¬C
(A ¬B) • ( ¬C A) • ( ¬D E)=
= ( ¬ A+¬B) • ( C +A) • ( D + E)=
= (¬ A+¬B) • ( C +A) • ( ¬B +¬C)=
= ¬ B+(¬ A • ¬C) • ( A + C )= ¬ B =1 ,
Значит B=0 , D=1 Сергей математик,
Следовательно, A =0
¬C A=1
C+A=1
C=1 Роман физик , а Петр химик Ответ: ХФМ
B 6 (повышенный уровень, время – 8 мин) Пример 6 (Вариант №4, 2009)
Три студента Антонов, Волков, Сергеев стремятся сдать сессию на отлично. Были высказаны следующие предположения:
- сдача экзаменов на отлично студентам Волковым равносильна тому, что сдаст на отлично Антонов или Сергеев;
- неверно, что сдаст на отлично Волков или одинаково на отлично сдадут Антонов и Сергеев;
- студент Сергеев не сдаст экзамены на отлично и это притом, что если Антонов сдаст на одни пятерки, то и Волков сдаст так же отлично.
После сессии оказалось, что только одно из трех предположений ложно. Кто сдал экзамены на отлично? В ответе укажите первые буквы фамилий студентов. Например, ответ АВС означает, что все трое сдали экзамены на одни пятерки.
B 6 (повышенный уровень, время – 8 мин) Пример 7
Андрей, Ваня и Саша собрались в поход. Учитель хорошо знавший этих ребят, высказал следующие предположения:
- Андрей пойдет в поход только тогда, когда пойдут Ваня и Саша.
- Андрей и Саша друзья, а это значит, что они пойдут в поход вместе или же оба останутся дома.
- Чтобы Саша пошел в поход, необходимо, чтобы пошел Ваня.
Когда ребята пошли в поход, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из названных ребят пошел в поход?
1
1
1
0
0
0
1
1
1
А v В С
А С v А С
С v В
- А В С
- А С v А С
- С В
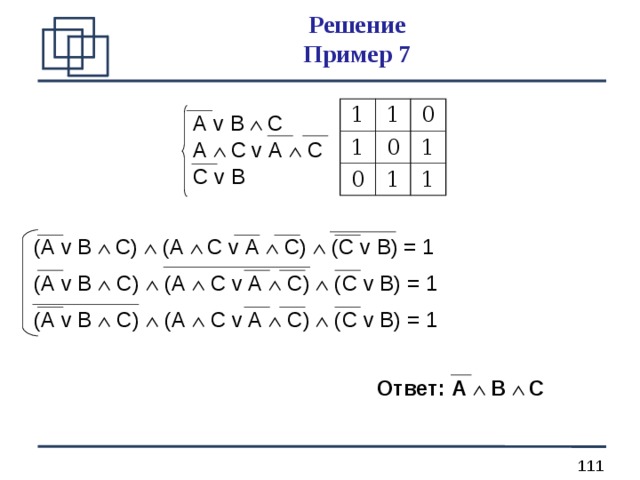
Решение Пример 7
1
1
1
0
0
0
1
1
1
А v В С
А С v А С
С v В
( А v В С ) ( А С v А С ) ( С v В ) = 1
( А v В С ) ( А С v А С ) ( С v В ) = 1
( А v В С ) ( А С v А С ) ( С v В ) = 1
Ответ: А В С
- Информационные ресурсы
- «Практикум по информатике и информационным технологиям», Н.Д. Угринович, Л.Л. Босова, М.: Бином. Лаборатория знаний, 2004
- «Информатика. Задачник- практикум в 2 т.», Под ред. И.Г. Семакина, Е.К. Хеннера, М.: Бином. Лаборатория знаний, 2002
- «Информатика: готовимся к ЕГЭ», Зеленко Л.С., Сопченко Е.В., Самара, 2008
- «ЕГЭ 2008. Информатика. Федеральный банк экзаменационных материалов», П.А. Якушкин, С.С. Крылов, М.: Эксмо, 2008
- «ЕГЭ 2009. Информатика.», Ярцева, Цикина, 2009
- «ЕГЭ 2009. Информатика - Универсальные материалы для подготовки учащихся», Крылов С.С, Лешинер В.Р, Якушкин П.А.
- Готовимся к ЕГЭ по информатике - Самылкина Н.Н.
- ЕГЭ Информатика : Раздаточный материал тренировочных тестов, Гусева И.Ю.
- ЕГЭ Информатика - ЕГЭ это просто! Молодцов В.А.
- ЕГЭ 2009 Информатика, Книга Сборник Экзаменационных заданий ЕГЭ 2009 ЭКСМО
- ЕГЭ 2009 Информатика, ЕГЭ 2009 по информатике от ФИПИ
- http:// kpolyakov.narod.ru
- http://www.ctege.org - Подготовка к ЕГЭ
- http://www.websib.ru/noos/informatika/ege.htm - Предметный сайт для учителей информатики.
- http://pedsovet.su/load/7 - " Сообщество взаимопомощи учителей", раздел по информатике.
111
"Основы логики". (3.88 MB)
0
1976
38
Нравится
0
