Тема. Основные понятия и формулы комбинаторики.
Комбинаторика – это область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Комбинаторные задачи – это задачи, требующие осуществления перебора всех возможных вариантов или подсчета их числа.
Правило сложения.
Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно m+n способами.
Задача 1. В классе 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение. 16+10=26 способов.
Задача 2. На тарелке 9 яблок и 8 апельсинов. Сколькими способами можно выбрать один фрукт?
Решение. 9+8=17 способов.
Правило умножения.
Пусть требуется выполнить последовательно (одно за другим) два действия, причем действие А можно выполнить m способами, а В – n способами, то оба действия вместе могут быть выполнены m·n способами.
Задача 3. В магазине есть 11 разных чашек и 8 разных блюдцев. Сколько вариантов чашки и блюдца можно купить?
Решение. 11·8=88 способов.
Задача 4. На тарелке 9 яблок и 8 апельсинов. Сколькими способами можно выбрать пару фруктов из одного яблока и одного апельсина?
Решение. 9·8=72 способа.
Факториал
Факториал n! – это произведение всех натуральных чисел от 1 до n включительно.
|
|
Пример 1. а) 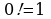 б)
б) 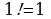 в)
в) 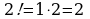 г)
г) 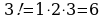
д) 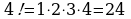 е)
е) 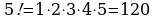
Сокращение факториалов.
Пример 2.
а) 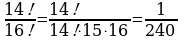 б)
б) 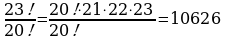
в) 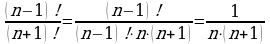
г) 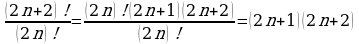
д) 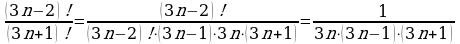
1. Размещения
Размещениями из n элементов по m элементов 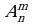 называются комбинации из n элементов по m элементов, которые отличаются друг от друга или самими элементами, или порядком элементов.
называются комбинации из n элементов по m элементов, которые отличаются друг от друга или самими элементами, или порядком элементов.
! Порядок важен!
|
|
Пример 3. Вычислить число размещений из 9 по 4.
Решение.
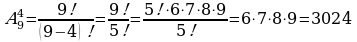
Пример 4. Вычислить: 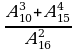
Решение.
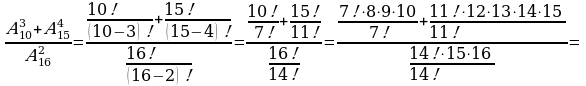
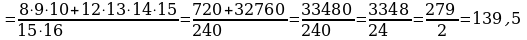
Задача 5. В первенстве по футболу участвует 17 команд. Разыгрываются медали: золото, серебро, бронза. Сколькими способами они могут быть разыграны?
Решение. Комбинации команд – победителей отличаются друг от друга составом и порядком следования элементов, т. е. являются размещениями из 17 по 3.
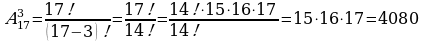
2. Перестановки
Перестановками из n элементов 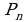 называются комбинации из одних и тех же n различных элементов, которые отличаются друг от друга только порядком следования элементов.
называются комбинации из одних и тех же n различных элементов, которые отличаются друг от друга только порядком следования элементов.
|
|
Пример 5. Вычислить число перестановок из 14 элементов.
Решение.
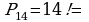 87178291200
87178291200
Пример 6. Вычислить: 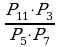
Решение.
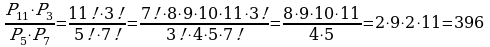
Задача 6. Сколькими способами можно расставить на полке 5 различных книг?
Решение. Имеем перестановки из 5 элементов.
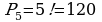 (способов)
(способов)
3. Сочетания
Сочетаниями из n элементов по m элементов 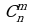 называются комбинации из n элементов по m элементов, которые отличаются друг от друга только составом элементов.
называются комбинации из n элементов по m элементов, которые отличаются друг от друга только составом элементов.
! Порядок не важен!
|
|
Пример 7. Вычислить число сочетаний из 9 по 4.
Решение.
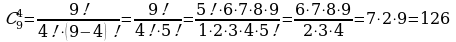
Пример 8. Вычислить: 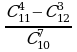
Решение.
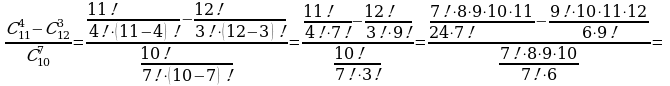
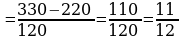
Задача 7. В первенстве по шахматам участвует 20 человек, а в финал выходят лишь трое. Сколькими способами можно определить эту тройку?
Решение. В данном случае порядок, в котором располагается эта тройка, не важен. Поэтому тройки, вышедшие в финал – это сочетания из 20 по 3.
Домашнее задание.
1) Вычислить число перестановок из 8 элементов.
2) Вычислить число сочетаний из 15 по 6.
3) Вычислить число размещений из 11 по 4.
4) Вычислить: 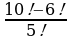
5) Вычислить: 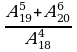
6) Вычислить: 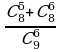

 Получите свидетельство
Получите свидетельство Вход
Вход


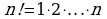
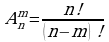
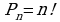
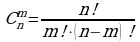









 Основные понятия и формулы комбинаторики (61.91 KB)
Основные понятия и формулы комбинаторики (61.91 KB)
 0
0 328
328 0
0 Нравится
0
Нравится
0







