Основные методы решения систем двух линейных уравнений с двумя переменными

Основные Методы решения систем линейных уравнений

с двумя переменными

7 класс

Ростов-на-Дону 2018 Г.

Цели урока:

• Обобщение знаний о методах решения систем линейных уравнений с двумя переменными
• Повторение и закрепление алгоритмов решения систем методом сложения и графическим методом
• Развитие навыков решения систем

Задачи урока:

• Образовательная: выработать прочные навыки решения систем двух уравнений с двумя неизвестными;
• Развивающая: развитие внимания и логического мышления, памяти, активизация самостоятельной деятельности;
• Воспитательная: способствовать развитию творческой деятельности учащихся, любознательности.

Разминка

• Актуализация опорных знаний. “ Без теории — нет практики”

А) Что такое система уравнений?

Б)Что называется решением системы уравнений?

В)Что значит решить систему уравнений?

Г)Назовите методы решения систем уравнения.

Д)Как решить систему уравнений графически?

Е)Как решить систему уравнений методом алгебраического сложения?

2. Решите уравнения

А) х - 8,1= 9,9 Б) 5х = -3,5 В) 3х – 7 = 2 Г) 3(х-7) = 2х + 4

3. Выразите у через х

А) 5х + у = 11 Б) 3х - у = 5 В) 10х + 5у = 5

Проверим результаты

1. Актуализация опорных знаний

А) Система уравнений -это уравнения, которые имеют одинаковые решения (х;y) и объединены фигурной скобкой.

Б) Решение системы - пара чисел (х;y) которая одновременно является решением и первого и второго уравнения системы.

В) Решить систему - это значит найти все ее решения или установить, что их нет.

Г) Графический метод, метод алгебраического сложения, метод подстановки.

Д) Нужно построить графики каждого уравнения на одной координатной плоскости и найти координаты точки пересечения этих графиков.

Е) Метод заключается в сложении двух уравнений системы почленно, с целью исключения одной переменной и сведению системы уравнений к одному линейному уравнению с одной переменной.

2. Решите уравнения

А) х = 18 Б) х = - 0,7 В) х = 3 Г) х = 25

3. Выразите у через х

А) у = 11-5x Б) у = 3x - 5 В) у = 1- 2x

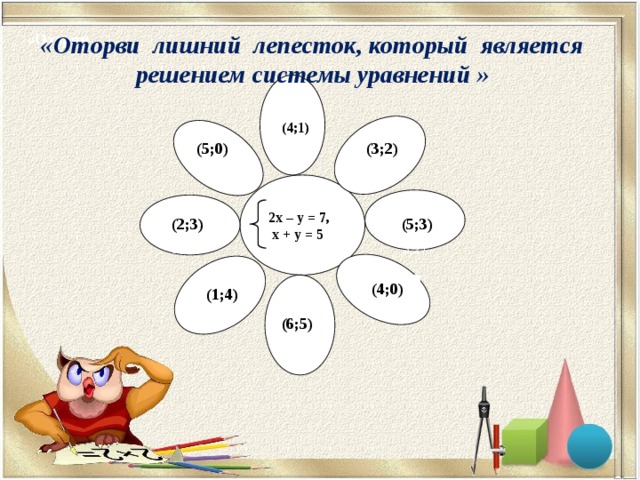
«Оторви лишний лепесток, который является решением системы уравнений »

«Оторви

(4;1)

(4;1)

(4;(1)

( )

(3;2)

(5;0)

3;2)

3;2)

2х – у = 7,

х + у = 5

(5;3)

(2;3)

3;2)

3;2)

(4;0)

(1;4)

3;2)

(6;5)

3;2)

Системы линейных уравнений

Метод

сложения

Метод

подстановки

Графический

метод

Решение системы графическим методом

х + у =5,

y = -x + 5,

- x + y =1;

y = х +1;

(2; 3)

Построим графики двух линейных уравнений в одной системе координат

y = х +1

y = -x + 5

х

х

y

y

1

1

2

4

2

2

3

3

Ответ: (2; 3).

Решение системы методом сложения

Сложим почленно

левые и правые части

уравнения

Найдем значение х

х + у=5,

- x + y =1;

х+3=5

х = 2;

2у = 6

Найдем значение у

у = 3

х = 2

y = 3;

Ответ: (2; 3).

Историческая справка :

ЕГИПЕТ. Первые задачи на составление и решение систем уравнений с

несколькими переменными встречаются в египетских и вавилонских текстах второго тысячелетия до нашей эры, а также в трудах древнегреческих и индийских ученых. Решались они различными искусственными способами, единого алгоритма не было.

КИТАЙ. Алгоритм решения систем линейных уравнений был напечатан в Китае в труде “Математика в девяти книгах” (206 г. до н.э.), где рассматривались системы и давились правила их решения. При этом все изложение словесно. Коэффициенты системы располагались на счетной доске в виде таблицы. При повторных действиях было замечено, что следует поступать по одному и тому же правилу систематически.

Первым появился способ сложения, а затем - способ подстановки. В книге

“ Всеобщая арифметика” (1707 г.) Ньютон излагает уже все способы решения систем, изучаемые ныне в школе.

Самостоятельная работа

1. Решить систему уравнений графическим методом

2х + у = 1

3х + у = 2

2. Решить систему уравнений методом алгебраического сложения

2х-3y=11

4х+5y=-11

3*. Решить систему одним из изученных методов

2(3х+2y)+9=4х+21

2х+10=3-(6х+5y)

Ответы:

1)(1;-1)

2) (1;-3)

3)(-4;5)

Решение задач с помощью систем уравнений

Расстояние между двумя пунктами по реке равно 80 км. Это расстояние

лодка проплывает по течению реки за 4 ч, а против течения – за 5 ч.

Найдите собственную скорость лодки и скорость течения реки?

Решение:

1 этап. Составление математической модели.

Пусть х ( км/ч ) – собственная скорость лодки, y ( км/ч ) – скорость течения реки. Заполним таблицу:

Составим систему уравнений:

(х + y)4=80

(х - y)5=80

S =vt

S, км

по течению

v, км/ч

против течения

80

t, ч

х+y

80

4

х-y

5

2 этап. Работа с математической моделью. Решение системы уравнений.

(х + y)4=80 : 4

(х - y)5=80 : 5

х + y=20 18+y=20

х - y=16 y=20-18

2х=36 : 2 y=2

х=18

х=18

y=2 - решение системы.

3 этап. Ответ на вопрос задачи.

18 км/ч- собственная скорость лодки

2 км/ч – скорость течения реки.

Игровой момент

Задумайте два числа. Найдите их сумму и их разность. Результаты сообщите мне, и я назову задуманные числа.

Решение:

Пусть задуманы числа х и у, тогда

х + y = a

х - y = в

Продолжи предложение:

• Сегодня на занятии я научился ………………………………..
• Мне понравилось …………………………………………….
• Я повторил …………………………………............................
• Я закрепил ………………………………….............................
• Я оцениваю свою работу на занятии на (хор., отл., уд.)
• Какие виды работ вызвали затруднения и требуют повторения ……………………………………………………
• В каких знаниях уверен………………………………………

СПАСИБО ЗА ВНИМАНИЕ !