Осевая и центральная симметрии

Осевая и центральная симметрии

Задачи нашего урока

Цель нашего урока

• понятия, связанные с центральной и осевой симметрией ;
• примеры фигур, обладающих центральной (осевой ) симметрией;
• обратить внимание на симметрию в архитектуре, живописи, технике, природе.

Симметрия – это соразмерность, наличие определённого порядка, закономерности в расположении частей. 

целеполагание

Математическая разминка

Математическая разминка

Симметрия

Симметрия

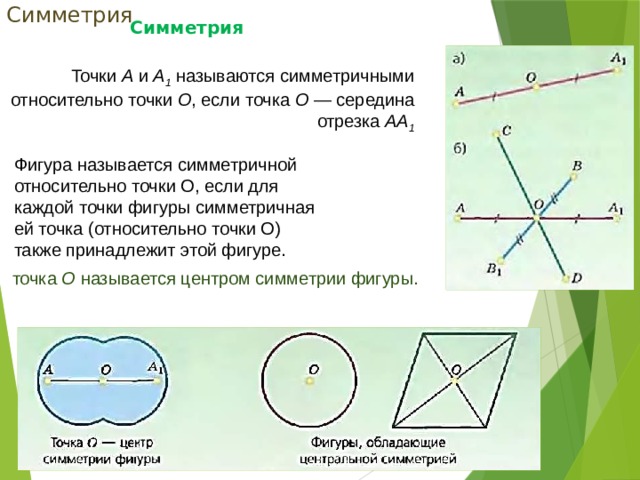
Точки А и А 1 называются симметричными относительно точки О , если точка О — середина

отрезка АА 1

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка (относительно точки О) также принадлежит этой фигуре.

точка О называется центром симметрии фигуры.

Симметрия

Симметрия

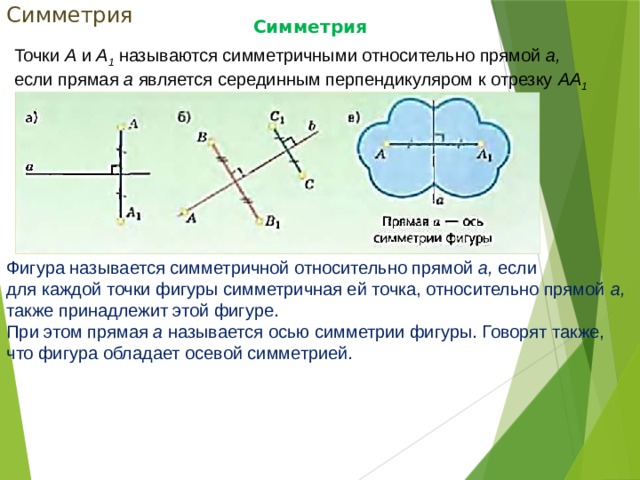
Точки А и А 1 называются симметричными относительно прямой а,

если прямая а является серединным перпендикуляром к отрезку АА 1

Фигура называется симметричной относительно прямой а, если

для каждой точки фигуры симметричная ей точка, относительно прямой а, также принадлежит этой фигуре.

При этом прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.

Отрабатываем алгоритмы

Работаем по алгоритму

Подумай

Подумайте!