Цель, задачи урока:
Научить строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией, формирование пространственных представлений учащихся.
Развитие умения наблюдать и рассуждать; развитие интереса к предмету через использование информационных технологий.
Развитие математической компетентности учащихся. Воспитание человека, умеющего ценить прекрасное.
Ожидаемый результат:
Ученики смогут строить симметричные фигуры относительно центра и прямой
Ход урока.
I. Организационный момент.
Сообщить тему урока, сформулировать цели урока.
II. Показ презентации: «Симметричный мир» (д/з учащихся)
III. Работа по теме урока (работа в группах)
Ученики самостоятельно выполняют задания. По завершению, обмениваются информацией.
1 вариант п. 47.
Осевая симметрия.
Осевая симметрия – это симметрия относительно____________
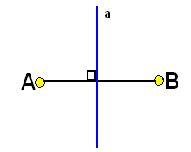
Две точки А и А1 называются симметричными относительно прямой а, если ____________
Прямая а называется_______________
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры, симметричная ей точка принадлежит_________
Равны ли симметричные относительно прямой фигуры?
Да. Нет.
2 вариант п. 47.
Центральная симметрия.

Центральная симметрия – это симметрия относительно________________
Две точки А и А1 называются симметричными относительно точки О, если_____________
Точка О называется_________________
Фигура называется симметричной относительно точки О, если для каждой точки фигуры, симметричная ей точка принадлежит________
Равны ли симметричные относительно точки фигуры?
Да. Нет.
Рассмотрим правила построения симметричных фигур.
1. Центральная симметрия – это симметрия относительно точки.
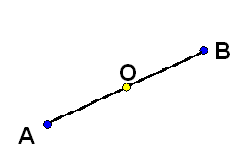
Точки А и В симметричны относительно некоторой точки О, если точка О является серединой отрезка АВ.
Точка О называется центром симметрии фигуры, а фигура называется центрально-симметричной.
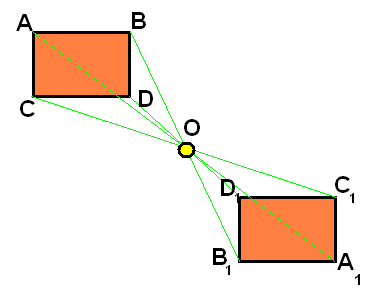
Построим треугольник А 1В 1 С 1, симметричный треугольнику АВС, относительно центра (точки) О.
Для этого:
Соединим точки А,В,С с центром О и продолжим эти отрезки;
2. Измерим отрезки АО, ВО, СО и отложим с другой стороны от точки О, равные им отрезки (АО=А 1 О 1, ВО=В 1 О 1, СО=С 1 О 1);
3. Соединим получившиеся точки отрезками А 1 В 1, А 1 С 1, В 1 С 1.
4. Получили ∆А 1 В 1 С 1 симметричный ∆АВС.
Точка О называется центром симметрии фигуры, а фигура называется центрально-симметричной.
Задание №1. На рисунке изображена часть фигуры, центром симметрии которой является точка М. Объясните ее построение.
Задание № 2. Проверьте правильность построения фигуры из №1 у соседа по парте. Постройте в его тетради четырехугольник и отметьте точку О, не принадлежащую этому четырехугольнику.
Возьмите свою тетрадь обратно и постройте четырехугольник, симметричный данному относительно точки О.
Проверьте правильность выполненного задания.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



 очка О называется центром симметрии фигуры, а фигура называется центрально-симметричной.
очка О называется центром симметрии фигуры, а фигура называется центрально-симметричной.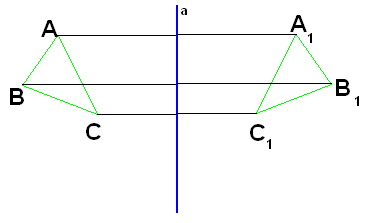
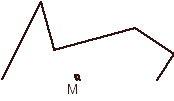












 Конспект урока по математике "Осевая и центральная симметрии" (0.28 MB)
Конспект урока по математике "Осевая и центральная симметрии" (0.28 MB)
 0
0 2650
2650 308
308 Нравится
0
Нравится
0


