

Симметрия. Симметрия и окружающий мир.
Осевая симметрия.
Построение элементарных фигур.
Практикум по решению задач.
Заключение.

Симметрия
(от греч. Symmetria – соразмерность).
Симметрия играет огромную роль в искусстве и архитектуре. Ее элементы можно заметить и в музыке, и в поэзии. Симметрия встречается в природе:
у кристаллов, растений, животных.
Она используется и в отдельных разделах математики, например, рассматриваемых построение графиков функций.



… В гранит оделася Не ва ;
Мосты повисли над во дами ;
Темнозелеными са дами
Ее покрылись остро ва …
Пушкин А.С. «Медный всадник»
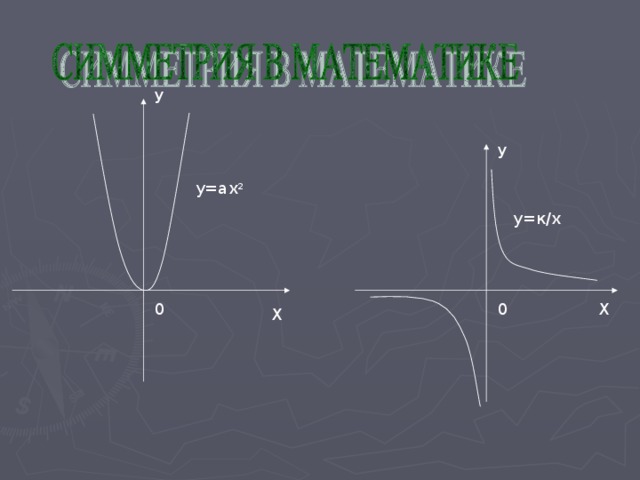
У
У
у=ах 2
у=к/х
0
Х
0
Х

а
Преобразование фигуры F в фигуру F ,
при котором каждая её точка Х переходит в точку Х , симметричную относительно данной прямой а , называется
преобразованием симметрии относительно прямой а или осевой симметрией .
Х
Х
Прямая а – ось симметрии
Х и Х - точки, симметричные относительно прямой а
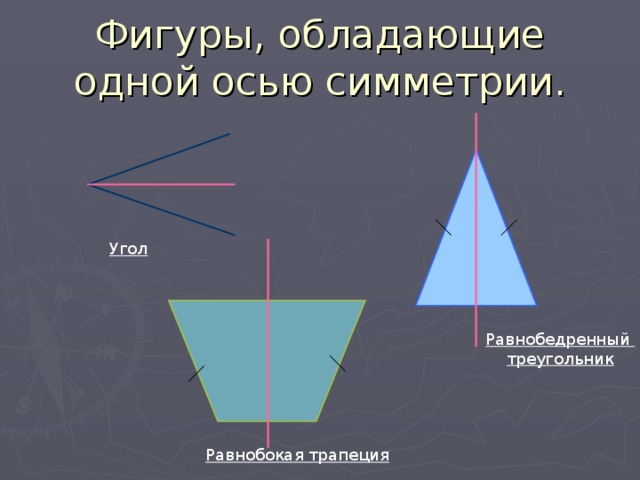
Фигуры, обладающие одной осью симметрии.
Угол
Равнобедренный
треугольник
Равнобокая трапеция
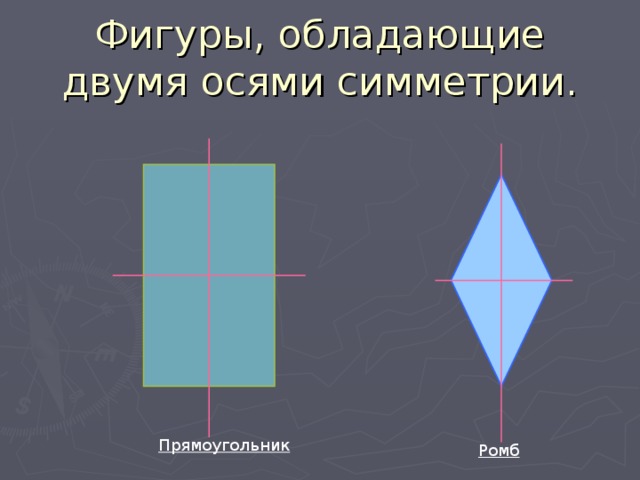
Фигуры, обладающие двумя осями симметрии.
Прямоугольник
Ромб
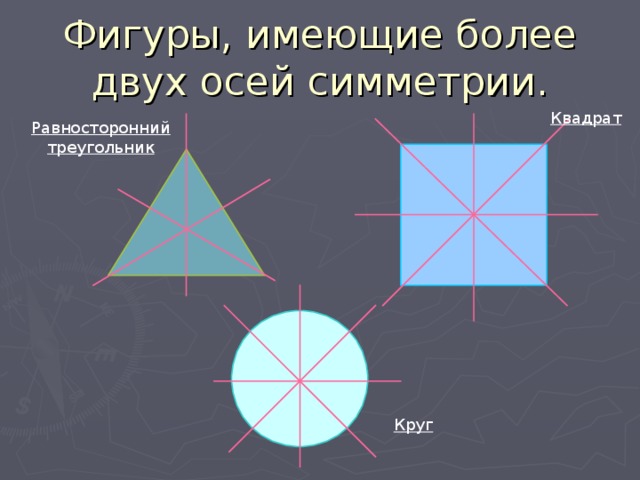
Фигуры, имеющие более двух осей симметрии.
Квадрат
Равносторонний треугольник
Круг
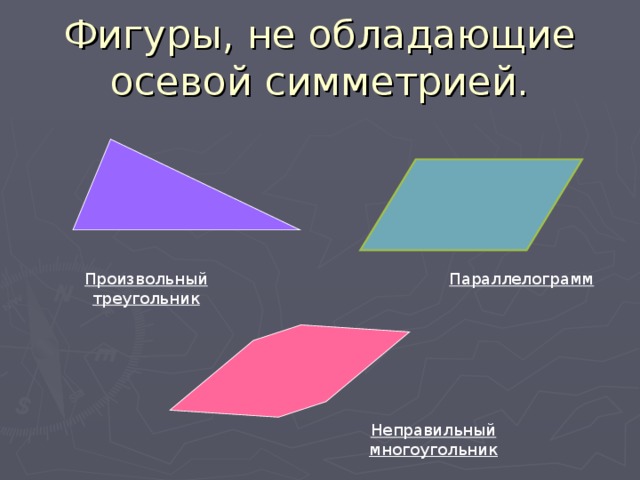
Фигуры, не обладающие осевой симметрией.
Произвольный треугольник
Параллелограмм
Неправильный многоугольник

Построение
ТОЧКИ, СИММЕТРИЧНОЙ ДАННОЙ
ОТРЕЗКА, СИММЕТРИЧНОГО ДАННОМУ
ТРЕУГОЛЬНИКА, СИММЕТРИЧНОГО ДАННОМУ
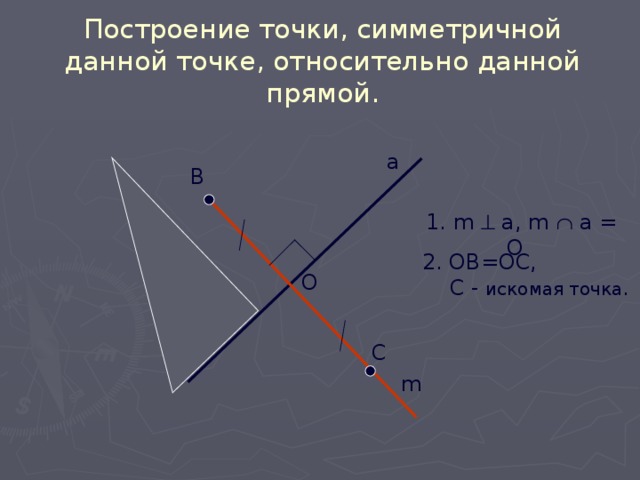
Построение точки, симметричной данной точке, относительно данной прямой.
а
В
1. m a, m a = O
2. OB=OC,
С - искомая точка .
О
С
m
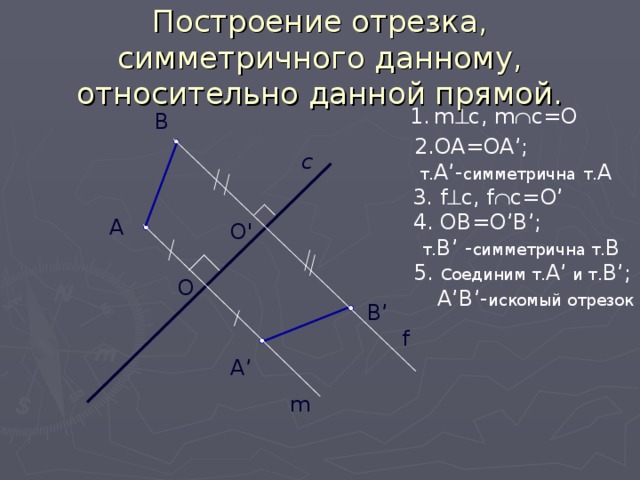
Построение отрезка, симметричного данному, относительно данной прямой.
В
2.OA=OA’;
т. А’- симметрична т. А
с
3. f c, f c=O’
4. ОВ=О’В’;
т. B’ - симметрична т. B
А
O'
5. Соединим т. А’ и т. В’;
А’В’- искомый отрезок
O
В’
f
А’
m
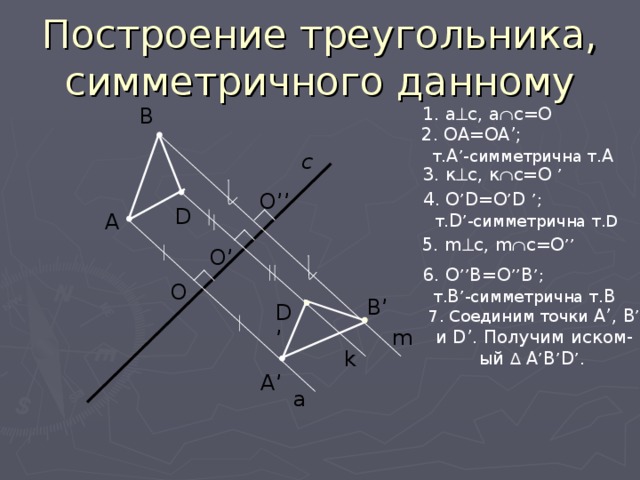
Построение треугольника, симметричного данному
1. a c, a c=O
В
2. OA=OA’;
т. А ’-симметрична т. А
с
3. к с, к с=О ’
4. О ’ D=O ’ D ’;
т. D ’-симметрична т.D
О’’
D
А
5. m c, m c=O ’’
О’
6. O ’’ B=O ’’ B ’;
т. В ’-симметрична т. В
О
В’
D’
7. Соединим точки А’, В ’
и D’. Получим иском-
ый ∆ А ’ В ’ D ’.
m
k
А’
a
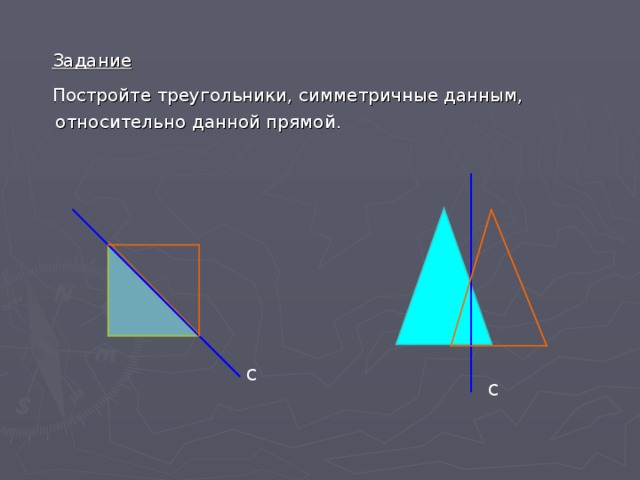
Задание
Постройте треугольники, симметричные данным,
относительно данной прямой.
с
с
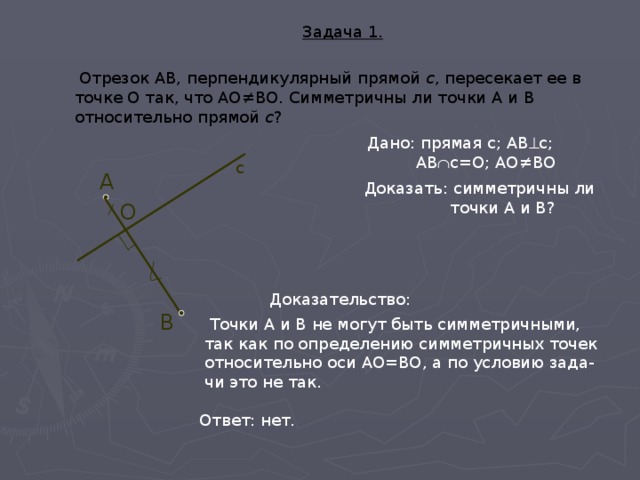
Задача 1.
Отрезок АВ, перпендикулярный прямой с , пересекает ее в точке О так, что АО≠ВО. Симметричны ли точки А и В относительно прямой с ?
Дано: прямая с; АВ с;
АВ с=О; АО≠ВО
с
А
Доказать: симметричны ли
точки А и В?
О
Доказательство:
В
Точки А и В не могут быть симметричными,
так как по определению симметричных точек
относительно оси АО=ВО, а по условию зада-
чи это не так.
Ответ: нет.
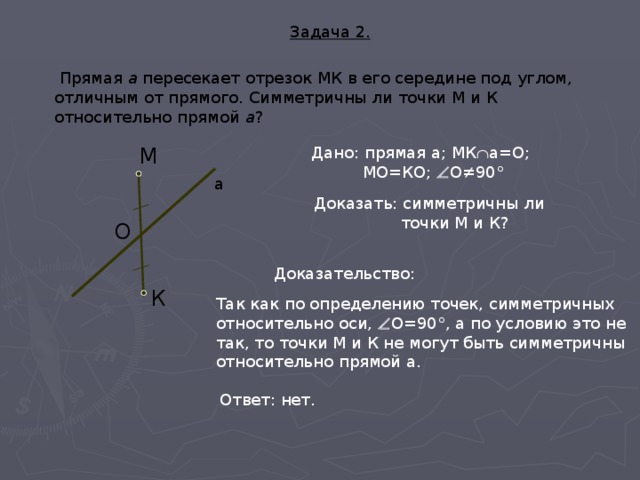
Задача 2.
Прямая а пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а ?
Дано: прямая а; МК а=О;
МО=КО; О≠90°
М
а
Доказать: симметричны ли
точки М и К?
О
Доказательство:
К
Так как по определению точек, симметричных
относительно оси, О=90°, а по условию это не
так, то точки М и К не могут быть симметричны
относительно прямой а.
Ответ: нет.
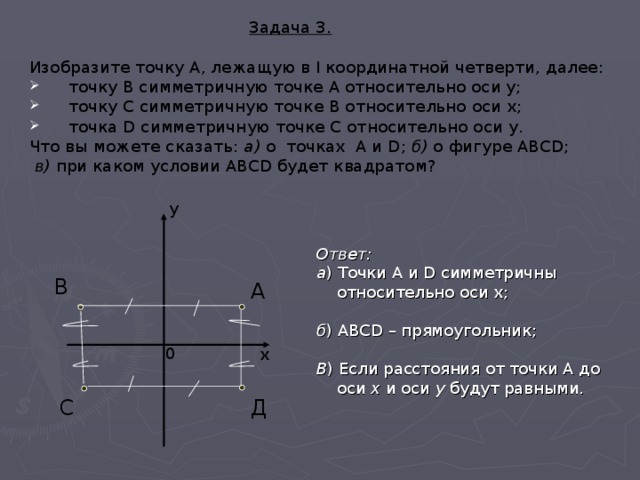
Задача 3.
Изобразите точку А, лежащую в I координатной четверти, далее:
- точку В симметричную точке А относительно оси y;
- точку С симметричную точке В относительно оси х;
- точка D симметричную точке С относительно оси у.
Что вы можете сказать: а) о точках A и D; б) о фигуре ABCD;
в) при каком условии ABCD будет квадратом?
у
Ответ:
а ) Точки A и D симметричны
относительно оси х;
б ) ABCD – прямоугольник;
В ) Если расстояния от точки А до
оси х и оси у будут равными.
В
А
0
х
Д
С

Задача 4.
Относительно какой из координатных осей симметричны точки М(7;2) и К(-7;2)?
- Задача 4. Относительно какой из координатных осей симметричны точки М(7;2) и К(-7;2)?
- Задача 4. Относительно какой из координатных осей симметричны точки М(7;2) и К(-7;2)?
Решение: Так как координаты х противоположны по
знаку, а l-7l=l7l, то точки М и К симметрич-
ны относительно оси у .
Ответ: симметричны относительно оси у .
Задача 5.
Точки А(5;…) и В(…;2) симметричны относительно
оси х . Запишите их пропущенные координаты.
- Задача 5. Точки А(5;…) и В(…;2) симметричны относительно оси х . Запишите их пропущенные координаты.
- Задача 5. Точки А(5;…) и В(…;2) симметричны относительно оси х . Запишите их пропущенные координаты.
Решение: Так как точки А и В симметричны относительно
оси х , то их абсциссы должны быть равны, а
ординаты отличаться по знаку. Тогда А(5;-2),
В(5;2).
Ответ: А(5;-2), В(5;2).

Задача 6.
Точка А(-2;3),точка В - симметричная ей точка относительно
оси х , точка С – симметричная точке В относительно у . Найдите координаты точки С.
- Задача 6. Точка А(-2;3),точка В - симметричная ей точка относительно оси х , точка С – симметричная точке В относительно у . Найдите координаты точки С.
- Задача 6. Точка А(-2;3),точка В - симметричная ей точка относительно оси х , точка С – симметричная точке В относительно у . Найдите координаты точки С.
Решение: Так как точки А и В симметричны относительно
оси х , их абсциссы равны, а ординаты отличаются
знаком. Тогда В(-2;-3). Поскольку точки В и С
симметричны относительно оси у , то их ординаты
равны, а абсциссы отличаются знаком. Значит,
С(2;-3).
Ответ: С(2;-3).

Симметрию можно обнаружить почти везде, если знать, как ее искать.
Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии.
Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».


 Получите свидетельство
Получите свидетельство Вход
Вход


































 Осевая симметрия (1.76 MB)
Осевая симметрия (1.76 MB)
 0
0 1364
1364 33
33 Нравится
0
Нравится
0




