Презентация по геометрии "Симметрия вокруг нас"

Симметрия (означает «соразмерность» ) - свойство геометрических объектов совмещаться с собой при определенных преобразованиях. Под симметрией понимают всякую правильность во внутреннем строении тела или фигуры.

История возникновения симметрии.

Впервые понятие симметрия появляется в VI веке до нашей эры в первой научной школе в истории человечества, у последователей Пифагора Самосского, пытавшихся связать симметрию с числом.

Каждой вещи, учили пифагорейцы, соответствует определенное отношение чисел, которое они называли логосом. Пифагорейцы предпочитали вместо слова «симметрии» пользоваться словом «гармония». 

Ученые древности, изучающие симметрию, любили обращаться к правильным многогранникам (грани у которых правильные многоугольники одного вида, а углы между гранями равны). Древние греки установили, что существует всего пять правильных выпуклых многогранников - тетраэдр (1), октаэдр (2), икосаэдр (3), куб (4), додекаэдр (5). Все правильные многогранники обладают зеркальной симметрией.

Осевая симметрия.

Осевая симметрия - это симметрия относительно прямой. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. В данном случае прямая - ось симметрии. Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.

Осевая симметрия есть у:

- треугольника;

- прямоугольника;

- ромба;

- квадрата;

- круга.

Центральная симметрия.

Центральная симметрия - симметрия относительно точки. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно  точки О также принадлежит  этой фигуре. В этом случае точка является центром симметрии фигуры. Две точки А и А1 называются симметричными относительно точки О, если  точка О - середина отрезка АА1 и перпендикулярна к нему. Точка О считается симметричной самой себе.

Центральная симметрия есть у:

- круга;

- параллелограмма.

Билатеральная симметрия.

Билатеральная симметрия (двусторонняя симметрия) — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны. Если на плоскость симметрии опустить перпендикуляр из точки A и затем из точки О на плоскости симметрии продолжить его на длину AО, то он попадёт в точку A1, во всём подобную точке A.

С имметрия является той идеей,

посредством которой человек на

протяжении веков пытался постичь и

создать порядок, красоту и совершенство.

Немецкий математик

Г.Вейль

В этом проекте Вы увидете:

• Понятие и историю возникновения симметрии
• Основные виды симметрии
• Симметричные фигуры
• Симметрию в быту, архитектуре, природе, религии, геометрии и др.

Проект подготовили ученики 8в класса

лицея №359: Аббасов Али, Захарова Катя

и Кобычев Александр.

Учитель математики: Налётова

Светлана Владимировна

Симметрия (означает «соразмерность» ) — свойство геометрических объектов совмещаться с собой при определенных преобразованиях. Под симметрией понимают всякую правильность во внутреннем строении тела или фигуры.

Впервые понятие симметрия появляется в VI веке до нашей эры в

первой научной школе в истории человечества, у последователей

Пифагора Самосского , пытавшихся связать симметрию с числом.

Каждой вещи, учили пифагорейцы, соответствует определенное

отношение чисел, которое они называли логосом . Пифагорейцы

предпочитали вместо слова «симметрии» пользоваться словом

«гармония» .

1

3

5

4

2

Ученые древности, изучающие симметрию, любили

обращаться к правильным многогранникам (грани у

которых правильные многоугольники одного вида, а углы

между гранями равны ). Древние греки установили, что

существует всего пять правильных выпуклых

многогранников - тетраэдр (1), октаэдр (2), икосаэдр (3),

куб (4), додекаэдр (5) . Все правильные многогранники

обладают зеркальной симметрией .

Осевая симметрия - это симметрия относительно прямой. Фигура называется симметричной относительно прямой а , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. В данном случае прямая - ось симметрии. Две точки А и А1 называются симметричными относительно прямой а , если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.

A

a

A 1

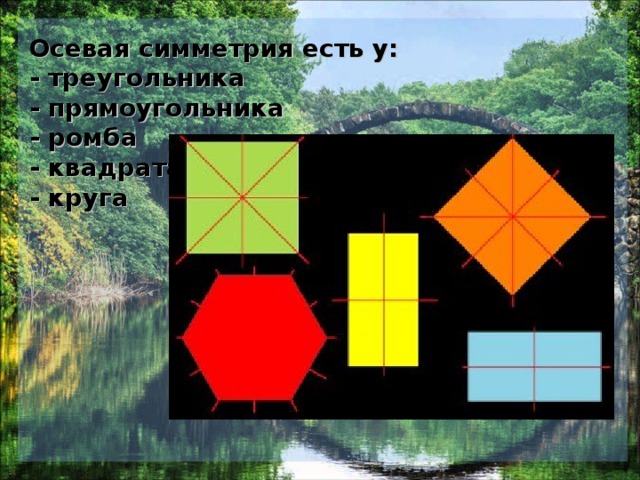
Осевая симметрия есть у: - треугольника - прямоугольника - ромба - квадрата - круга

О

A 1

A

Центральная симметрия - симметрия относительно точки. Фигура

называется симметричной относительно точки О , если для каждой

точки фигуры симметричная ей точка относительно точки О также

принадлежит этой фигуре. В этом случае точка является центром

симметрии фигуры.

Две точки А и А1 называются симметричными относительно точки О, если точка О - середина отрезка АА1 и перпендикулярна к нему.

Точка О считается симметричной самой себе.

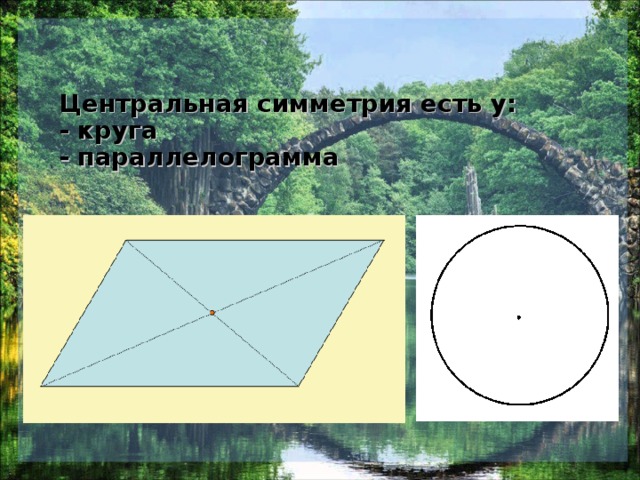
Центральная симметрия есть у:

- круга

- параллелограмма

Билатера́льная симметрия (двусторонняя симметрия) — симметрия зеркального отражения, при которой объект имеет одну плоскость

симметрии, относительно которой две его половины зеркально

симметричны. Если на плоскость симметрии опустить

перпендикуляр из точки A и затем из точки О на плоскости

симметрии продолжить его на длину AО, то он попадёт в точку A1, во всём подобную точке A.

А

О

А1

Ось симметрии у билатерально симметричных объектов отсутствует. У животных билатеральная симметрия проявляется в схожести или

почти полной идентичности левой и правой половин тела. При этом всегда существуют случайные отклонения от симметрии (например, расположение родинок или отклонения в расположении внутренних органов).

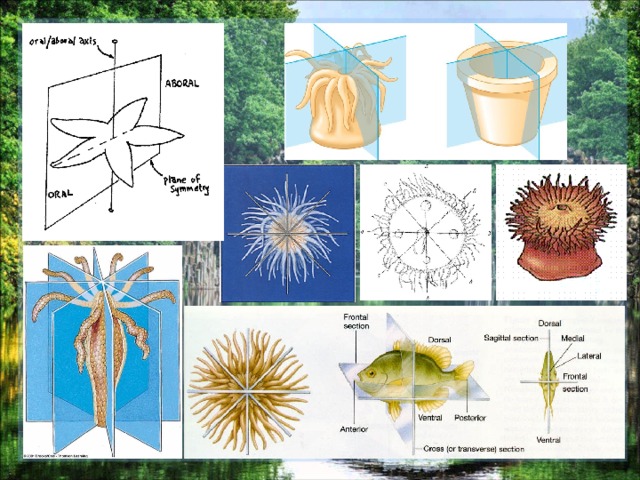
Радиальная симметрия — форма симметрии, при которой тело (или фигура) совпадает само с собой при вращении объекта вокруг

определённой прямой . Центром симметрии объекта называют

прямую, на которой пересекаются все оси двусторонней симметрии. Радиальной симметрией обладают такие геометрические объекты, как круг, шар, цилиндр или конус.

Не только истинный поэт, но и истинный математик

одинаково озабочены отбором слов и фраз для более

точного выражения мысли.

А.Блок

Замечательным примером зеркальной симметрии в литературе

являются слова фразы " перевертыши ":

• Шалаш, казак, дед, потоп .
• " А роза упала на лапу Азора ". В этом "перевертыше" центром

зеркальной симметрии является буква " н ", относительно которой

все остальные буквы (не учитывая пропуски между словами)

расположены во взаимно противоположной очередности.

• " Кинь лед зебре, бобер бездельник ." В этом "перевертыше"

центром зеркальной симметрии является буква " о ".

• " А луна канула " Центр зеркальной симметрии - буква " к ".

Такие "перевертыши" в литературе называют палиндромами .

Зеркальную симметрию равнобедренного треугольника мы находим в

стихотворении Валерия Брюсова “Треугольник ” .

Я,

Еле

Качая

веревки,

в синели

не различая

синих тонов

и милой головки,

летаю в просторе,

крылатый как птица,

меж липовых кустов!

но в заманчивом взоре

знаю, блещет, алея, зарница!

и я счастлив ею без слов!

Чередование рифм и чтение по интонации дает чувствовать прелесть

(симметрии) пушкинского стихотворения .

А.С. Пушкин.

В этот год осенняя погода

Стояла долго на дворе

Зимы ждала, ждала природа

Снег выпал только в январе.

Произведение А. Н.Воронихина Казанский собор в Санкт-Петербурге

Большой дворец в Петергофе

Смольный собор

Адмиралтейство

Аничков мост

Зимний дворец в Санкт-Петербурге

Фотография Захаровой Кати

Фонарь на улице Итальянской

города Санкт-Петербурга

Фотография Аббасова Али

Храм Спаса-на-крови в Санкт-Петербурге

Фотография Кобычева Саши

Потолоки Эрмитажа

Пример симметрии у кошки

Фотография Захаровой Кати

Фотография Аббасова Али

Склонность людей видеть цель в симметрии, является одной из

причин, почему симметрия часто является неотъемлемой частью

символов мировых религий. До сих пор симметрия подчиняется

правилу: она посылает сигналы «мы одинаковые», а асимметрия

выражает мысль «я особый, лучше чем ты». Взаимоотношения со

сверстниками строятся на основе симметрии, а властные

отношения — на асимметрии.

Вывод

В процессе изучения нами симметрии мы узнали много нового о мире, в котором мы живем. Мы увидели симметрию в таких простых вещах, как в обычном мяче, конфете, фонарном столбе и вообще практически везде!

Также мы увидели симметрию в животных и цветах, стихотворениях и в прозе, в молекулах и в атомах, в архитектуре и живописи, и даже в самом человеке.

На уроках геометрии отводится очень мало времени для изучения симметрии, но благодаря этому проекту мы буквально прониклись в эту тему. Нам помогали наши одноклассники, родители и наши любимые учителя. Без них бы у нас не получилось такого многообразного проекта.

Симметрия противостоит хаосу, беспорядку. Она присутствует

в нашей жизни буквально во всём, но мы настолько к ней привыкли,

что не замечаем этого. Но как бы мы к ней не относились, она есть в

нашей жизни, добавляя в неё мир, спокойствие и состояние чего-то не

чуждого глазу. Это доказали наши исследования. Мы считаем, что

элементы симметрии всегда будет вокруг нас.

Мы будем с удовольствием продолжать заниматься нашим проектом, изучать симметрию еще глубже.