Урок-презентация проекта по математике «Симметрия вокруг нас»

Цели:

Показать значение принципа симметрии в алгебре.

Выявить архитектурные стили, представленные в Коломне.

Научиться определять виды симметрии в природе.

Познакомить учащихся с понятиями «асимметрия», «диссимметрия», «антисимметрия».

Ответить на вопросы:

Во всем ли в жизни симметрия?

Только ли симметрия является признаком красоты?

Общепедагогические задачи:

Формирование у учащихся практической направленности в изучении предметов геометрии, алгебры, истории архитектуры, природы и умения применять полученные знания на практике.

Развитие у учащихся креативности мышления, умения наблюдать, сравнивать, анализировать и делать выводы, отстаивать свою точку зрения.

Воспитание бережного отношения к историческому и культурному наследию страны ; трудолюбия, умения работать в команде, толерантности.

Оборудование:

компьютер;

интерактивная доска;

мультимедийный проектор;

План урока:

Организационный момент.

Активизация знаний. Теоретический блиц-опрос.

Защита учебных проектов.

Подведение итогов работы над проектом.

Домашнее задание.

Ход урока.

На доску вынесены эпиграфы к уроку:

«Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство».

Герман Вейль

1. Организационный момент.

Учитель. «Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем оно основано? Разве во всем в жизни симметрия?» Мы попытаемся ответить на эти вопросы Николеньки Иртеньева, устами которого их задает нам сам Лев Толстой в повести «Отрочество».

Сегодня у нас заключительный этап работы над межпредметным проектом «Симметрия вокруг нас». Почему возникла необходимость в таком проекте? Искусство и творчество вам ближе, нежели те теоретические знания, которые вы получаете на уроках, в частности, геометрии, алгебры. В большинстве своем вы считаете их ненужными, не имеющими применения в вашей будущей профессии. Поэтому целями данного проекта и сегодняшней презентации являются: (слайд 2). А работать мы сегодня будем по следующему плану: (слайд 3). Эпиграфом презентации вашей работы могут быть слова великого математика и физика рубежа XIX-XX веков Германа Вейля (зачитывает).

2. Активизация знаний. Теоретический блиц-опрос.

Итак, блиц-опрос для проверки компетентности наших экскурсоводов (слайды 4-6)

Что понимается под движением ?

Приведите примеры движений?

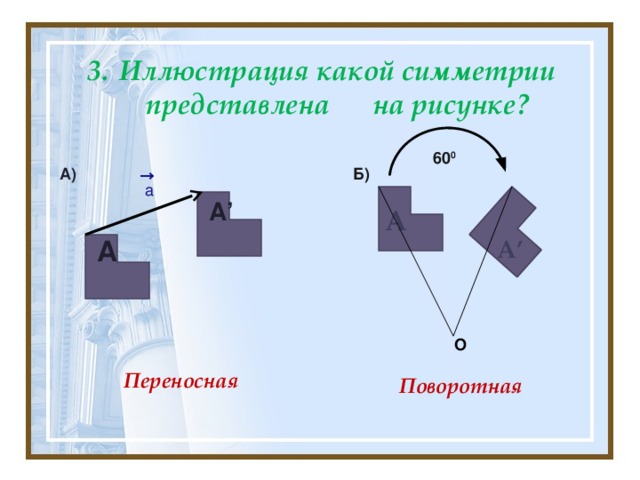
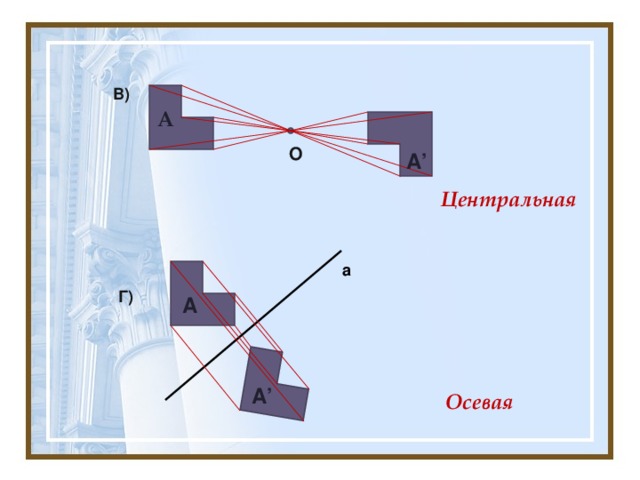
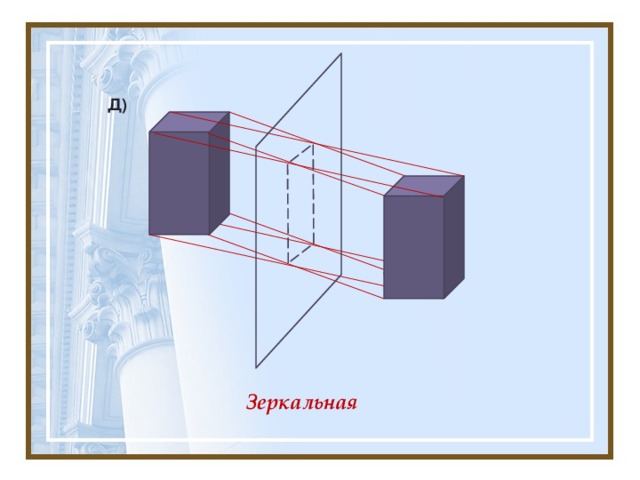
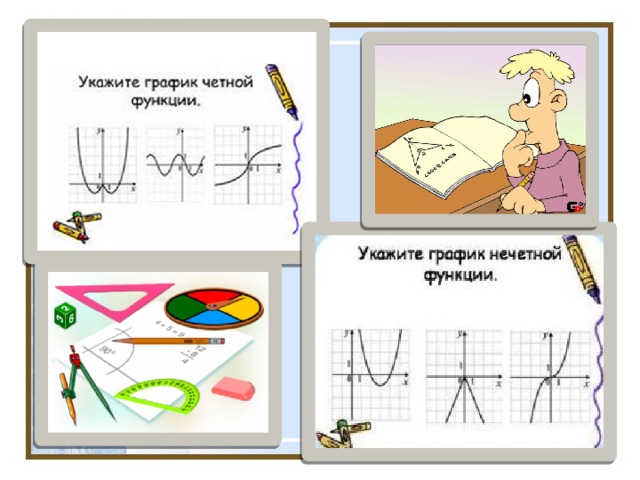
Иллюстрация какой симметрии представлена на рисунке?

Ну что ж, молодцы, я думаю, все готовы к защите проекта.

3. Защита учебных проектов.

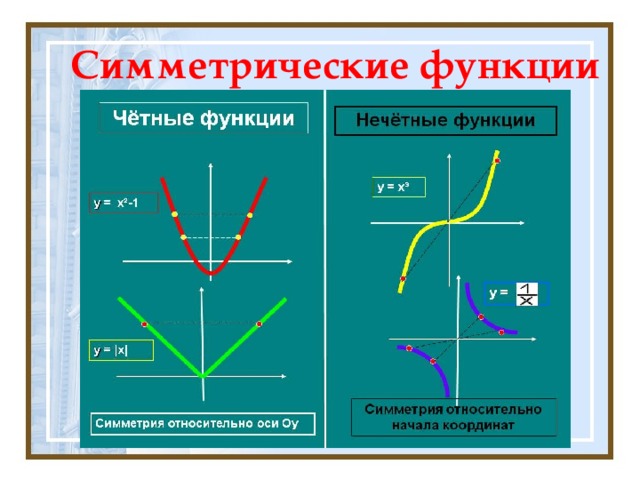
Выступление 1 группы. Учащиеся демонстрируют симметрию в алгебре (Симметрические функции, решение возвратных уравнений 3 и 4 степени, симметрические многочлены и решение симметрических систем 2 степени).

Выступление 2 группы.

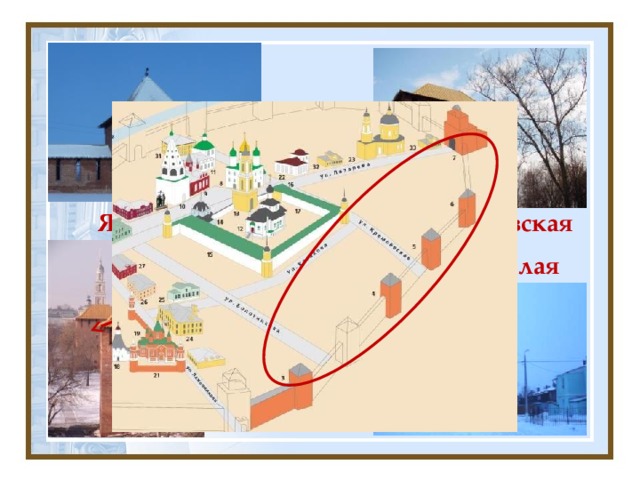
На примере Маринкиной башни иллюстрируется переносная и поворотная симметрия – 20-го порядка

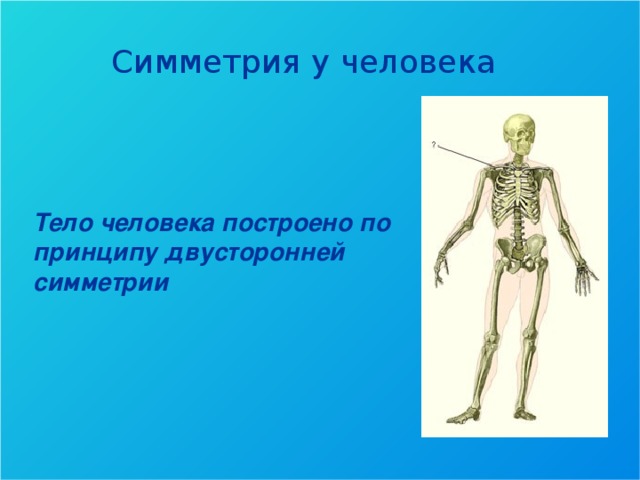
Выступление 3-й группы. Учащиеся демонстрируют различные виды симметрий в живой и неживой природе. А также формулируют понятия «асимметрия», «диссимметрия», «антисимметрия». Демонстрируется выполненный учащимися этой группы эксперимент с нарушением симметрии на примере лица человека.

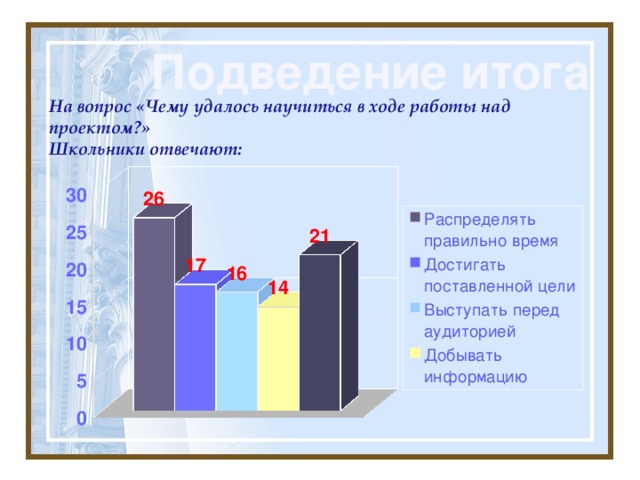
4. Подведение итогов.

Учитель: Сегодня вы показали презентацию своей работы. Продуктами нашего проекта стали слайды презентации У нас получился интересный разговор. Наши ребята смогли ответить на вопрос Николеньки Иртеньева. Конечно не всюду нас окружает симметрия. Но вернемся к вопросу, поставленному в начале урока: «Только ли симметрия является признаком красоты?». Класс делает вывод о том, что нужно согласиться, что в жизни есть место не только симметрии, но и ее частичному или полному отсутствию и от этого окружающий нас мир более гармоничен и красив. Т.о. наше мнение таково, что симметрия является объективным, но не единственным признаком красоты.

Школьники отвечают на вопрос: «Чему удалось научиться в ходе работы над проектом?»

5. Домашнее задание.

На блоге http://borushova1972.blogspot.com скачать кроссворд и ответ отправить на электронный ящик [email protected]

Спасибо вам за вашу творческую работу.

Урок-презентация проекта «Симметрия вокруг нас» Над проектом работали учащиеся 9-го класса Руководитель проекта: учитель математики Борюшова Е.А.

«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни симметрия?»

Лев Николаевич Толстой

Цели урока:

• Выявить значение принципа симметрии в

алгебре.

• Выявить архитектурные стили,

представленные в Коломне.

• Научиться определять виды симметрии в природе.
• Познакомиться с понятиями «асимметрия»,

«диссимметрия», «антисимметрия».

• Ответить на вопросы:

1)Во всем ли в жизни симметрия?

2)Только ли симметрия является признаком

красоты?

План урока

• Теоретический блиц-опрос

• Защита учебных проектов

• Подведение итогов работы над проектами
• Домашнее задание

Симметрия…является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. Г. Вейль

Блиц-опрос

• Что понимается под движением?

2. Приведите примеры движений.

• Иллюстрация какой симметрии представлена на рисунке?

60 0

А)

→

Б)

а

А

А’

А’

А

О

Переносная

Поворотная

В)

А

О

A’

Центральная

a

Г)

A

A’

Осевая

Д)

Зеркальная

Защита

проектов

Проект 1 группы:

«Симметрия в алгебре».

Проект подготовили:

Гвоздева А.

Каплун В.

Ковальчук О.

Онуфриенко А.

Пономаренко К.

Ковалева У.

Маликов И.

Курбанова А.

Симметрия в алгебре

• Функция называется чётной, если справедливо равенство

• График чётной функции симметричен относительно оси

ординат .          .

• Функция называется нечётной, если справедливо равенство

• График нечётной функции симметричен относительно начала координат   
• График нечётной функции симметричен относительно начала координат   

Пример 1.

Доказать, что у = х 4 — четная функция.

Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.

Пример 2.

Доказать, что у = х 3 ~ нечетная функция.

Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.

Симметрические функции

Возвратные уравнения 3-й и 4-й степени

• Многочлены n-ой степени f (x) = a n x n + a n-1 x n-1 + … + a 0 называется возвратным , если его коэффициенты, одинаково отдаленные от начала и от конца, равны между собой.
• Алгебраическое уравнение вида f (x) = 0, где f (x) – возвратный многочлен , называют возвратным уравнением .

2x 3 +7x 2 +7x+2 = 0

2x 3 +2+7x 2 +7x = 0

2 (x 3 +1) +7x (x+1) = 0

2 (x+1) (x 2 –x+1) + 7x (x+1)=0

(x+1) (2x 2 - 2x+2+7x)=0

(x+1) (2x 2 +5x+2)=0

x+1=0 или 2x 2 +5x +2 =0

x= -1 D= 25 - 16=9

x₁ = -2

x₂ = - 0,5

Ответ:-1;-2;-0,5.

6z 2 -35z+50=0

6х 4 -35х 3 +62х 2 -35х+6х 2 =0

Д=b 2 -4ac=(-35) 2 -4*6*50= 1225-1200= 25

Z 1 = 5 / 2

6х 2 -35х+62- 35 / х +6=0

Z 2 = 10 / 3

6х 2 + 6 / х 2 -35х- 35 / х +62=0

х+ 1 / х = 5 / 2 х+ 1 / х = 10 / 3

6(х 2 + 1 /х 2 )-35(х+ 1 / х )+62=0

Х+ 1 / х =z

х+ 1 / х - 5 / 2 =0 х+ 1 / х - 10 / 3 =0

(х+ 1 / х ) 2 =z 2

2х 2 -5х+2=0 х  0 3х 2 -10х+3=0

Х 2 +2+ 1 / х 2 =z 2

Д=25-4*2*2=9 Д= 100-4*3*3=64

Х 2 + 1 / х 2 =z 2 -2

Х 1= ½ х 2 = 2 Х 3= 1 / 3 Х 4 = 3

6(z 2 -2)-35z+62=0

6z 2 -12-35z+62=0

Ответ:1/2;2;1/3;3.

Системы уравнений второй степени.

Система уравнений второй степени – это система уравнений, в которой есть хотя бы одно уравнение второй степени.

Укажите симметричные многочлены:

• X 3 +4x 2 y+4xy 2 +y 3

• 3x 4 -8x 3 y+3y 4

• X 5 +Y 5

• 2x 4 +7x 3 y+7xy 3 +2y 4

Литература

1. Виленкин Н.Я.Алгебра :издательство «Просвещение» Москва, 1968.

2. Интернет – ресурсы:

http://ru.wikipedia.org/wiki/

http://festival.1september.ru/

3 Болтянский В.Г. и др. Симметрия в алгебре. - М.: Наука, 1967.

4 Башмаков М.И. Уравнения и неравенства. - М.: Наука, 1971.

5 Березин В.Н. и др. Сборник задач для факультативных

и внеклассных занятий по математике. Книга для учителя. - М.: Просвещение, 1985.

6 Вавилов В.В. и др. Задачи по математике. Алгебра. - М.: Наука, 1987.

7 Черкасов О.Ю. и др. Математика: Справочник для старшеклассников

и поступающих в вузы. - М.: АСТ-Пресс, 2001.

8В.Г.Болтянский, Н.Я.Виленкин Симметрия в алгебре. 2-е издание

9 Винберг Э. Б. Симметрия многочленов. - М.: МЦНМО,

2001. — 24 с: ил. (Серия: «Библиотека „Математическое просвещение"»).

Проект 2 группы:

Симметрия в архитектуре «Вдоль Кремлевской стены».

Проект подготовили:

Тихонова В.

Вялых И.

Гурина В.

Швец С.

Короткова В.

Вельчев Н.

Вдоль Кремлевской стены

« Чувство симметрии и реальное стремление его выразить в быту и в жизни существовало в человечестве с палеолита…

Этот опыт многих тысяч поколений ясно

указывает на глубокую эмпирическую основу этого понятия…»

Академик В.И.Вернадский

(1863 – 1945 гг)

« Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии… применение симметрии в первобытном производстве определялось не столько эстетическими мотивами, но в известной мере и уверенностью человека в большей пригодности для практики правильных форм.»

Академик А. В. Шубников

(1887 – 1970 гг)

Архитектурные стили

готика

барокко

классицизм

ампир

конструктивизм

эклектика

футуризм

модерн

хай-тек

Маринкина башня

Грановитая башня

Ямская

Семеновская

Погорелая

Спасская

Пятницкие

ворота

• История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;

• История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;

• История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;

Литература

1.Большаков М.В. Декор и орнамент в книге: Альбом. - М.: Книга,

1990.

2. Волошинов А. В. Математика и искусство. - М.: Просвещение, 2000.

3. Гильде В. Зеркальный мир. — М.: Мир, 1982г. 4. Данилова Г.И. Мировая художественная культура. От истоков до

XVII века: учебник для 10 класса общеобразовательных учреждений

гуманитарного профиля, 3 изд. - М.: Дрофа, 2006

5. Пилявский В.И., Тиц А.А., Ушаков Ю.С. История Русской архитектуры. Стройиздат, 1984.

6 Интернет-ресурсы:

http://festival.1september.ru/

http://www.kolomna-kreml.ru/

http://ru.wikipedia.org/wiki/

Проект 3 группы:

«Симметрия в природе»

Проект подготовили:

Бугаёва Оксана,

Пизикс Алёна,

Кравченко Катя,

Имерели Данил,

Пизикс Андрей,

Жигалов Саша,

Трапезников Коля,

Боровиков Саша,

Конограев Максим,

Гелеверя Вадик.

Симметрия в природе

Симметрия в природе

Симметрия является важнейшим свойством природы . Поразительные по красоте примеры симметрии дают снежинки.

Снежинка обладает поворотной симметрией.

Симметрия у животных

Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии.

радиальная (лучистая)

билатеральная

Симметрия в биологии

В XX веке усилиями российских учёных - В Беклемишева, В Вернадского, В Алпатова, Г.Гаузе - было создано новое направление в учении о симметрии - биосимметрика

На примере дерева просматривается симметрия конуса

Симметрия в биологии

У цветковых растений в большинстве проявляется радиальная и билатеральная симметрия. Цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей.

Симметрия у человека

Тело человека построено по принципу двусторонней симметрии

Диссимметрия — это частично расстроенная симметрия,

противоречивое единство симметрии и асимметрии, обозначающее некоторый упорядоченный отход от симметрии;

это асимметрия внутри симметрии и наоборот.

Антисимметрия – это сохранение одного свойства объекта и замена другого свойства на противоположное .

Асимметрия –

это отсутствие

симметрии.

Асимметрия –

это отсутствие

симметрии.

• История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;

• История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;

• История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;

Литература

• Гильде В. Зеркальный мир. — М.: Мир, 1982г
• Интернет-ресурсы:

http://festival.1september.ru/

http://ru.wikipedia.org/wiki/

Подведение итога

На вопрос «Чему удалось научиться в ходе работы над проектом?» Школьники отвечают:

Домашнее задание

На блоге http://borushova1972.blogspot.com скачать кроссворд и ответ отправить на электронный ящик [email protected]