Образовательный маршрут по теме «Обыкновенные дроби»
математика 5 класс по учебнику Г.В. Дорофеев, И.Ф. Шарыгин
Целое


|
|
|
|


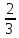 – обыкновенная дробь, состоит из числителя и знаменателя.
– обыкновенная дробь, состоит из числителя и знаменателя.
3- знаменатель дроби, показывает на сколько равных частей разделили целое.
2 – числитель дроби, показывает сколько таких частей взяли.
Черта дроби означает - деление
Умение: Сравнивать дроби с одинаковым знаменателем
| Правило сравнения дробей: |
| Из двух дробей с одинаковым знаменателем больше та, у которой числитель больше, и меньше та, у которой числитель меньше. |
Пример: Сравните дроби 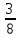 и
и 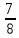
Решение: согласно правилу сравниваем числители, так как 3
Ответ: 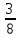
2.Умение: Находить дробь от числа.
| Правило нахождения дроби от числа |
| Чтобы найти дробь от числа нужно это число разделить на знаменатель дроби, а затем результат умножить на числитель дроби. |
Пример 1: Найти 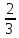 от 90
от 90
Решение: 1) Так как знаменатель дроби показывает на сколько частей разделили целое, то 90 ∶ 3 = 30 (нашли одну третью часть)
2) Так как числитель дроби показывает сколько таких частей взяли, то 30 ∙ 2 = 60 (нашли две третьих части)
Ответ: 60
Пример 2: Сколько сантиметров в 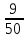 метра?
метра?
Решение: 1 метр = 100 см
100 : 50 = 2 (см) в
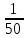 метра
метра2 ∙ 9 = 18 (см) в
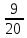 метра
метра
Ответ: 18 см
Умение: Выполнять сложение и вычитание дробей с одинаковыми знаменателями.
| Правило сложения и вычитания дробей с одинаковыми знаменателями |
| Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Чтобы вычесть дроби с одинаковым знаменателями, нужно из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.
|
Пример: Сложите дроби 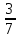 и
и 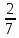
Решение: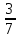 +
+ 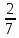 =
= 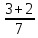 =
= 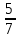
Ответ: 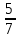
Пример: Выполни действие 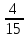 -
-
Решение: 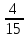 -
- =
=
Ответ:
Умение: Выделять целую часть из неправильной дроби.
| Правило выделения целой части из неправильной дроби |
|
Пример: Выдели целую часть из дроби
Решение: 1) 20: 3 = 6 (остаток 2)
=6
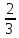
Ответ: 6 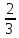
Умение: Представлять смешанное число в виде неправильной дроби.
| Правило: Чтобы представить смешанное число в виде неправильной дроби, нужно
|
Пример: Запишите смешанную дробь 4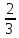 в виде неправильной дроби:
в виде неправильной дроби:
Решение:
4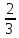 =
= =
Ответ:
Умение: Выполнять сложение и вычитание смешанных чисел.
При сложении(вычитании) смешанных чисел нужно помнить, что смешанное число – это сумма натурального числа и дроби, например
2 = 2+
| Правило: При сложении (вычитании) смешанных чисел целые части складывают (вычитают ) отдельно, а дробные – отдельно. |
Возможные случаи:
2
+3
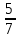 = (2 + 3)+(
= (2 + 3)+(+
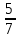 ) = 5 +
) = 5 += 5
Ответ: 5
При сложении смешанных чисел дробная часть оказалась неправильной дробью. В таком случае из неё необходимо выделить целую часть и добавить к уже имеющейся целой части.
2 + 3
= (2 + 3) + (
+
) = 5 +
= 5 + 1
=6
Ответ: 6
При вычитании смешанных чисел дробная часть уменьшаемого оказалась меньше дробной части вычитаемого. В таком случае нужно «занять» единицу из целой части уменьшаемого и представить его дробную часть в виде неправильной дроби с нужным знаменателем. Затем выполнить вычитание.
6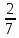 -2
-2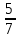 =(5 +1
=(5 +1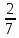 ) - 2
) - 2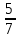 =(5 +
=(5 + ) - 2
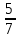 =5
=52
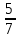 = 3
= 3
Ответ: 3
Вычитание из натурального числа дроби или смешанного числа
а)1-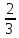 =
= -
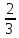 =
=
Ответ:
б) 8 - 3 = 7
- 3
= 4
Ответ: 4
Умение: Анализировать текст задачи и моделировать условие.
При решении задачи сначала внимательно читается текст. Каждое предложение задачи несёт в себе определённую информацию, которую необходимо использовать при решении. На первом этапе составляется краткая запись условия задачи (математическая модель). На втором этапе используя наши знания по математике мы решаем задачу. На третьем этапе отвечаем на вопрос задачи. Задача может иметь несколько способов решения, но ответ должен быть у всех способов одинаковый.
Пример:
В первый день в магазине было продано
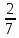 части всего мороженого, а во второй – на
части всего мороженого, а во второй – на больше. Какая часть мороженого была продана за эти два дня?
Решение:
1-й день - 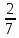 ч.
ч.
2-й день - ? ч. на ч больше, чем
Какая часть мороженого была продана за два дня?
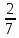 +
+ =
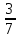 (части) мороженого продали во второй день.
(части) мороженого продали во второй день.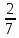 +
+ 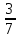 =
= 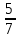 (ч) мороженого продали за два дня.
(ч) мороженого продали за два дня.
Ответ: 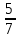 части.
части.
Умение: Находить число по его дроби.
| Правило: Чтобы найти число по его дроби, нужно это число разделить на числитель дроби, а затем результат умножить на знаменатель дроби. |
Пример: Найди число, если его равны 24.
Решение:
24 ∶ 8 = 3 (узнали
часть)
3· 11 =33 (нашли
, то есть всё число)
Ответ: 33

 Получите свидетельство
Получите свидетельство Вход
Вход



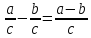









 Образовательный маршрут по теме "Обыкновенные дроби" (38.64 KB)
Образовательный маршрут по теме "Обыкновенные дроби" (38.64 KB)
 0
0 206
206 8
8 Нравится
0
Нравится
0


