МАТЕМАТИКА
Уроки для 5 класса Л.Н.Трубицына
Тема. Угол. Обозначения углов
Цель: формировать понятие «угол», «вершина», «стороны угла», «биссектриса угла», знакомство с обозначением углов; формировать у учащихся умение строить угол; различать углы на готовых рисунках и обозначать углы разными способами.
Тип урока: усвоение новых знаний.
Оборудование: таблица-схема «Углы. Измерение углов».
Ход урока
I. Актуализация опорных знаний
Устные упражнения
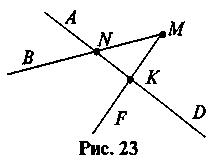
1. Назовите все лучи, которые вы видите на рис. 23. Назовите пары лучей, имеющих общее начало.
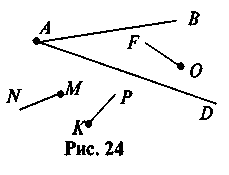
2. Какие из лучей на рис. 24 пересекают лучи АВ и АС?
3. Чему равна длина одного звена ломаной, которая состоит из 16 равных звеньев и имеет длину 90 см?
4. Чтобы сделать ограждение для своего огорода квадратной формы, Аленка отрезал 4 куска проволоки. Как проверить, что эти 4 куски подойдут девочке (будут равными)?
II. Формирование новых знаний
План изложения учебного материала
1. Понятие угла
2. Элементы угла
3. Обозначения углов
4. Понятие луча, проходящего между сторонами угла
5. Понятие равных углов
6. Понятие биссектрисы угла
1-3. Объяснение учитель сопровождает построением угла и в тетрадях и на доске, учащиеся делают такие записи.
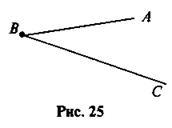
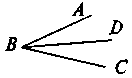
Лучи ВА и ВС выходят из точки В.
Тогда ABC - угол, ВА и ВС - стороны, В - вершина угла.
Угол обозначается ![]() CBA или
CBA или ![]() ABC, или
ABC, или ![]() В.
В.
(Желательно букву В выделить контрастным цветом.)
На закрепление этого материала устно выполняются упражнения.
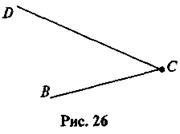
1) Какое из обозначений угла на рис. 26 является правильным?
a) ![]() DBC; б)
DBC; б) ![]() CDB; в)
CDB; в) ![]() BCD; г)
BCD; г) ![]() C.
C.
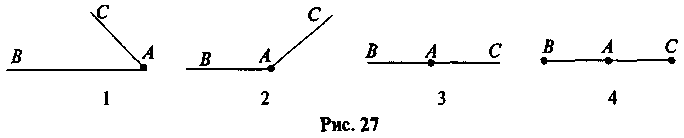
3) Какова из фигур на рис. 27 лишняя?
4. Понятие луча, что проходит между сторонами угла
Понятие луча, проходящего между сторонами угла не дается строго (как в 7 классе), но желательно объяснить ученикам, что должно выполняться 2 условия: луч исходит из вершины угла, проходит между сторонами, то есть любой отрезок с концами на сторонах угла будет пересечен этим лучом.
На закрепление понятие устно выполняются упражнения.
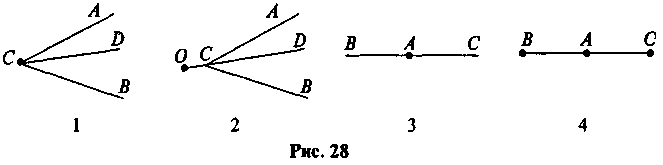
На каком из рисунков луч не проходит между сторонами угла АСВ? (рис. 28)
5-6. На закрепление понятие равных углов и биссектрисы угла - практическое задание. Учитель заранее готовит бумажные модели углов (рис. 29).
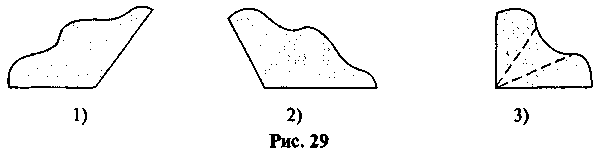
Задача 1. Как на модели угла 1) построить бісектрису угла? [Перегнуть так, чтобы образовались два углы, которые совмещаются, линия перегиба - биссектриса.]
Задание 2. Как угол 2) разделить на 4 равные части? [Перегнуть так, как в задании 1, а затем образованный еще раз так же перегнуть.]
Задача 3. На модели 3) проведено 2 лучи так, что, перегнувши углы по этих лучах, получим 3 углы, которые совпадают при наложении. Можно лучи, обозначенные на модели, назвать бісектрисами данного угла? Почему? Есть они бісектрисами каких-то других углов?
III. Закрепление материала
Далее по учебнику решаем задачи.
1) №№ 297; 299; 301 - на закрепление нового материала;
2) №№ 307; 308; 293 - на повторение.
Дополнительно: логическая упражнение. Назовите пропущенное число и рисунок.
|
| 3 |
|
|
| 6 | 9 |
|
| 9 | 9 |
IV. Итог урока
Отвечая на вопрос № 296, учащиеся еще раз называют основные понятия, рассматриваемые на уроке.
V. Домашнее задание
п. 11, № 296 (устно); 298; 300; 302.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Обозначения углов (36.42 KB)
Обозначения углов (36.42 KB)
 0
0 568
568 22
22 Нравится
0
Нравится
0










