Об аксиомах геометрии

Так как геометрия строится на аксиомах, следует дать определение этому понятию.

Второй слайд представляет собой, собственно, определение аксиомы. Первая аксиома говорит о том, что одну и только одну прямую можно провести через две точки.

Можно предложить школьникам построить две разные прямые через две точки. Тогда, им будет очевидно, что эта аксиома верна. Разумеется, доказать ее невозможно, на то она и называется аксиомой.

Второе утверждение об отрезках, которые лежат на луче и имеют начало в вершине луча. Такой отрезок определенной длины можно построить только один.

То есть два одинаковых отрезка, начинающихся с вершины луча начертить невозможно. И третья аксиома посвящена углам.

От любого луча можно отложить угол (в определенном направлении), равный определенному неразвернутому углу.

Опять же, школьникам можно предложить опровергнуть эту аксиому. Этот урок поможет лучше закрепить, понять и «поверить» в аксиому.

Исходные положения, на основе которых доказываются теоремы, называются аксиомами.

Например, аксиомой является утверждение о том, что через любые две точки проходит прямая, и притом только одна.   

Сравнение двух отрезков мы проводили с помощью наложения одного отрезка на  другой. Возможность такого наложение вытекает из следующей аксиомы: на любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

Сравнение двух углов основано на аналогичной аксиоме: от любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.

Об аксиомах геометрии

с

а

2

4

3

b

1

Выполнил: учитель математики и информатики МБОУ «Ясно-Полянская ООШ», Зубово-Полянского района, Республики Мордовия, Куприянов А.С.

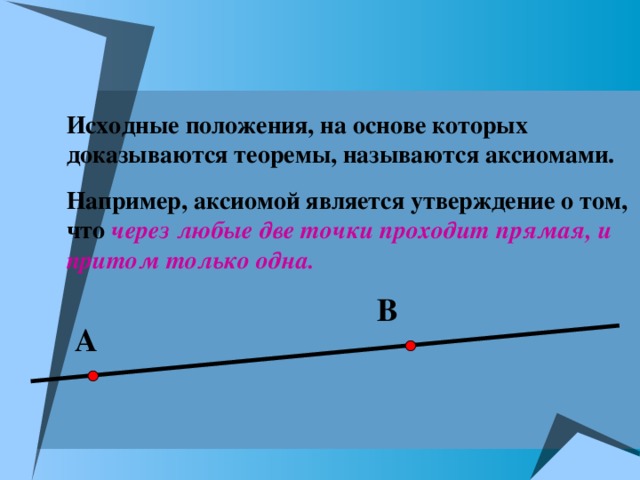
Исходные положения, на основе которых доказываются теоремы, называются аксиомами.

Например, аксиомой является утверждение о том, что через любые две точки проходит прямая, и притом только одна.

В

А

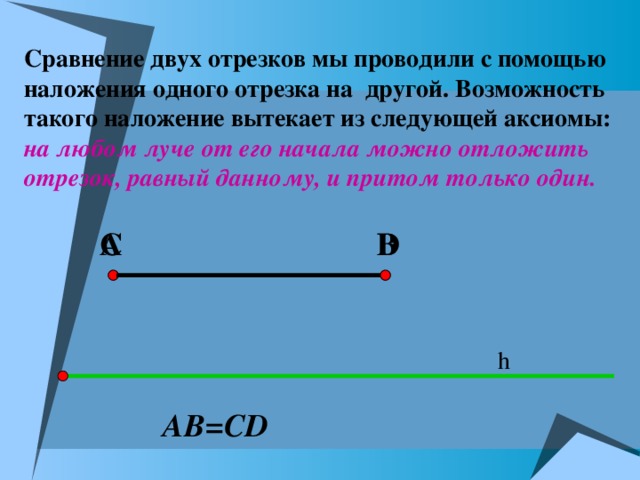
Сравнение двух отрезков мы проводили с помощью наложения одного отрезка на другой. Возможность такого наложение вытекает из следующей аксиомы: на любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

С

D

А

B

h

AB=CD

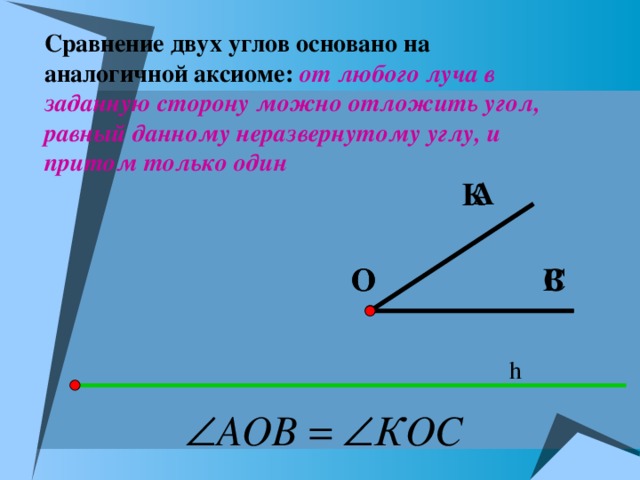
Сравнение двух углов основано на аналогичной аксиоме: от любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один

А

К

B

О

О

С

h

Само слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».

Такой подход к построению геометрии, когда сначала формируются исходные положения-аксиомы, а затем на их основе путем логических рассуждений доказываются другие утверждения, зародился еще в глубокой древности и был изложен в знаменитом сочинении «Начало» древнегреческого ученого Евклида (примерно 365-300гг. до н.э.). Сама геометрия, изложенная в «Началах», называется евклидовой геометрией.

Сочинение Евклида «Начало» состояло из 15 книг. В 1-й книге формулируются исходные положения геометрии, а также содержатся основополагающие теоремы планиметрии.

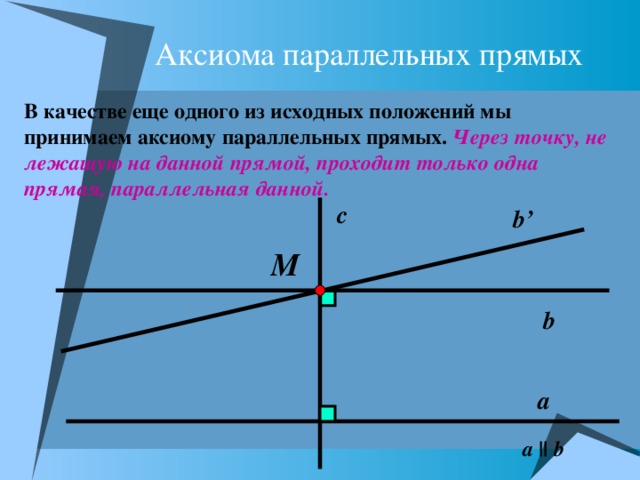
Аксиома параллельных прямых

В качестве еще одного из исходных положений мы принимаем аксиому параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

с

b’

М

b

а

a || b

Многие математики, начиная с древних времен, предпринимали попытки доказать пятый постулат Евклида, т.е. вывести его из других аксиом. Однако эти попытки каждый раз оказывались неудачными. И лишь в прошлом веке было окончательно выяснено, что утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой. Огромную роль в решении этого вопроса сыграл великий русский математик Николай Иванович Лобачевский (1792-1856)

ЛобачевскийНиколай Иванович

Перейти к биографии

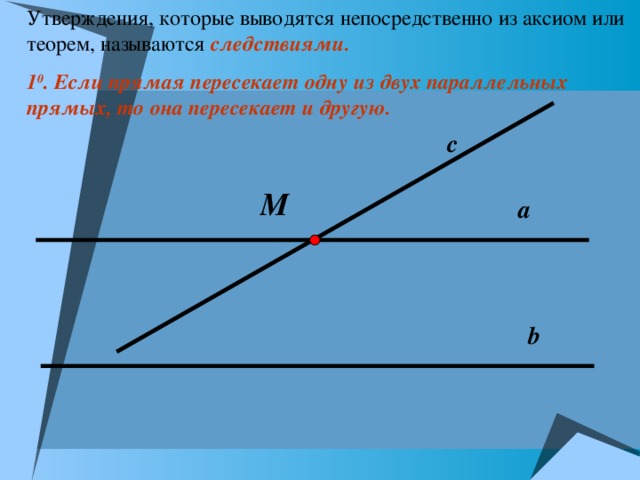
Утверждения, которые выводятся непосредственно из аксиом или теорем, называются следствиями.

1 0 . Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

с

М

а

b

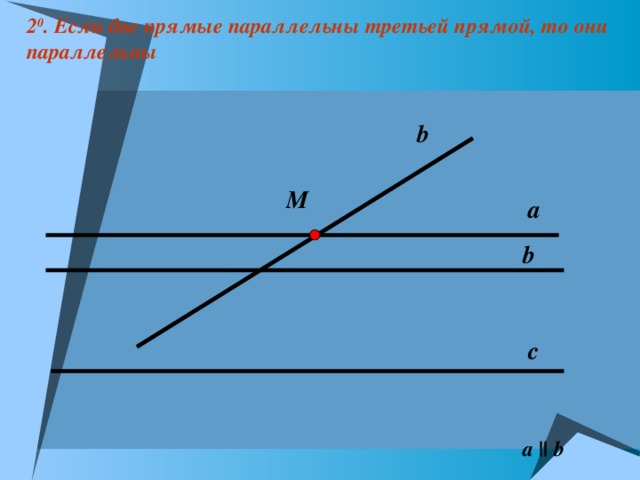
2 0 . Если две прямые параллельны третьей прямой, то они параллельны

b

М

а

b

с

a || b

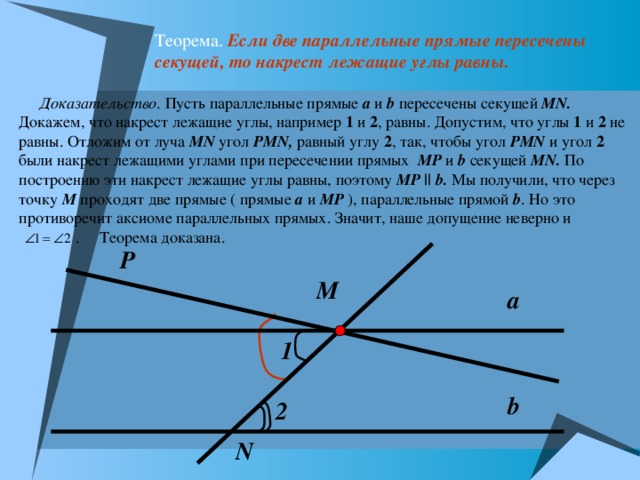
Теорема. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Доказательство . Пусть параллельные прямые a и b пересечены секущей MN . Докажем, что накрест лежащие углы, например 1 и 2 , равны. Допустим, что углы 1 и 2 не равны. Отложим от луча MN угол Р MN , равный углу 2 , так, чтобы угол Р MN и угол 2 были накрест лежащими углами при пересечении прямых M Р и b секущей MN . По построению эти накрест лежащие углы равны, поэтому M Р || b . Мы получили, что через точку M проходят две прямые ( прямые a и M Р ), параллельные прямой b . Но это противоречит аксиоме параллельных прямых. Значит, наше допущение неверно и . Теорема доказана.

Р

М

а

1

b

2

N

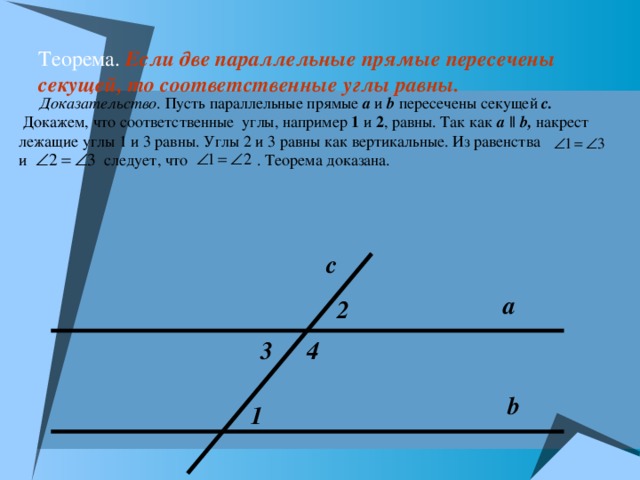
Теорема. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Доказательство . Пусть параллельные прямые a и b пересечены секущей с. Докажем, что соответственные углы, например 1 и 2 , равны. Так как a || b , накрест лежащие углы 1 и 3 равны. Углы 2 и 3 равны как вертикальные. Из равенства и следует, что . Теорема доказана.

с

а

2

4

3

b

1

Теорема. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 0 .

с

а

2

4

3

b

1

• Прямые а и b параллельны, 5 = 40 0 .

Какие еще углы равны 40 0 ?

с

а

2

1

4

3

b

5

6

8

7

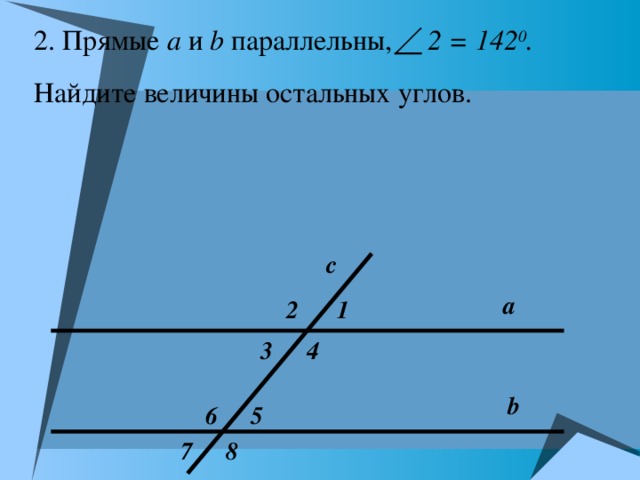
2. Прямые а и b параллельны, 2 = 142 0 .

Найдите величины остальных углов.

с

а

1

2

3

4

b

6

5

8

7

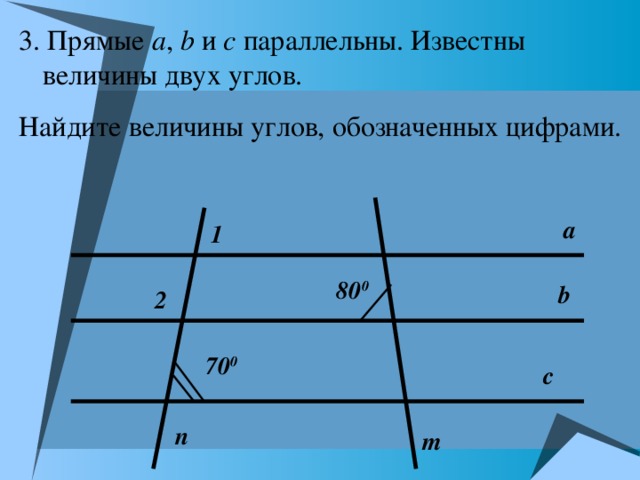
3. Прямые а , b и с параллельны. Известны величины двух углов.

Найдите величины углов, обозначенных цифрами.

а

1

80 0

b

2

70 0

с

n

m

• Разность двух внутренних односторонних углов при двух параллельных прямых и секущей равна 30 0 . Найдите эти углы.
• Сумма двух накрест лежащих углов при пересечении двух параллельных прямых и секущей равна 150 0 . Чему равны эти углы?
• Один из внутренних односторонних углов при двух параллельных прямых и секущей в 3 раза больше другого. Найдите эти углы.
• Домашнее задание: № 209 и № 210

ЛОБАЧЕВСКИЙ Николай Иванович (1792-1856), российский математик, создатель неевклидовой геометрии (геометрии Лобачевского). Открытие Лобачевского (1826, опубликованное 1829-30), не получившее признания современников, совершило переворот в представлении о природе пространства, в основе которого более 2 тыс. лет лежало учение Евклида, и оказало огромное влияние на развитие математического мышления. Родился в небогатой семье мелкого служащего. Почти вся жизнь Лобачевского связана с Казанским университетом, в который он поступил по окончании гимназии. В 1846 стал ректором университета.

При Лобачевском Казанский университет достиг расцвета. Обладавший высоким чувством долга, Лобачевский брался за выполнение трудных задач и всякий раз с честью выполнял возложенную на него миссию.

По инициативе Лобачевского начали издаваться «Ученые записки Казанского университета» (1834), были организованы астрономическая обсерватория и большой физический кабинет.

Величайшим научным подвигом считается создание им первой неевклидовой геометрии, историю которой принято отсчитывать от заседания Отделения физико-математических наук в Казанском университете 11 февраля 1826, на котором Лобачевский выступил с докладом «Сжатое изложение основ геометрии со строгим доказательством теоремы о параллельных».

Лобачевский исходил из допущения, согласно которому через точку, лежащую вне данной прямой, проходит несколько прямых, не пересекающихся с данной прямой. Развивая следствия, проистекающие из этого допущения, которое противоречит знаменитому V постулату (в других вариантах 11-ой аксиоме) «Начал» Евклида, Лобачевский не убоялся сделать дерзкий шаг, перед которым из опасения противоречий останавливались его предшественники: построить геометрию, противоречащую повседневному опыту и «здравому смыслу» — квинтэссенции повседневного опыта.

Открытие Лобачевского поставило перед наукой по крайней мере два принципиально важных вопроса, не поднимавшихся со времен «Начал» Евклида: «Что такое геометрия вообще? Какая геометрия описывает геометрию реального мира?». До появления геометрии Лобачевского существовала только одна геометрия — евклидова, и, соответственно, только она могла рассматриваться как описание геометрии реального мира. Ответы на оба вопроса дало последующее развитие науки. Лобачевский вошел в историю математики не только как гениальный геометр, но и как автор фундаментальных работ в области алгебры, теории бесконечных рядов и приближенного решения уравнений.

Интернет ресурсы

http://www.pomogala.ru/matematika/geometria_7_9_atanasyan.html

http://ucheba.dlldat.com/docs/index-5154.html

http://eslovar.com.ua/russkaya_istoriya/page/lobachevskiy.5563