НОД и НОК натуральных чисел, применение в решении задачи №19 ЕГЭ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ САРАТОВСКОЙ ОБЛАСТИ

Государственное автономное учреждение дополнительного профессионального образования

«Саратовский областной институт развития образования»

Кафедра математического образования

НОД и НОК натуральных чисел, применение в решении задачи

№19 ЕГЭ

Выпускная творческая работа

слушателя курсов повышения квалификации

по дополнительной профессиональной программе

«Теоретические основы и методика обучения математике

в общеобразовательных организациях (с использованием ДОТ)»

учителя математики МОУ «СОШ п. Сергиевский Саратовского района Саратовской области»

Мизякиной Ольги Сергеевны

Руководитель

доцент кафедры

математического образования,

Кривобок В.В., к.ф.м.н.

Саратов 2016

Содержание

Введение............................................................................................................3 стр

Глава I. Теоретические основы вычисления НОД и НОК............................5 стр

1.1. НОД и НОК................................................................................................5 стр

1.2. Алгоритм Евклида.....................................................................................7 стр

1.3. Нахождение НОД и НОК с помощью разложения на простые

множители...................................................................................................9 стр

Глава II. Методический опыт, практическое применение НОД и НОК....14 стр

2.1. Как НОК и НОД чисел помогает решать интересные и

разнообразные задачи.............................................................................14 стр

2.2. Примеры решения задач № 19 ЕГЭ через нахождение

НОД и НОК ..................................................................................................19 стр

Заключение.....................................................................................................23 стр

Список использованных источников...........................................................24 стр

Введение

Актуальность исследования. В последнее время от школы и учителя требуют не только дать знания, сформировать программные умения и навыки у всех учащихся, но и научить ребят творчески распоряжаться ими. Современный учитель должен владеть технологиями обучения, направленными на активизацию познавательной деятельности школьников. Поэтому необходимо найти такие способы организации процесса обучения, которые будут ускорять развитие учащихся и при этом учитывать возможности каждого ребёнка. Особенно это важно в старших классах при подготовке к ЕГЭ. Нужно найти такие методы и формы организации деятельности учащихся, чтобы они могли заинтересовать учащихся в том, чтобы им хотелось решать тесты, чтобы они их не боялись решать и в дальнейшем могли успешно сдать ЕГЭ.

Тема моей работы актуальна, так как задачи в целых числах давно включены в КИМы ЕГЭ по математике и оцениваются максимальным количеством баллов, что не маловажно для результата по экзамену. Также задачи такого типа встречаются на олимпиадах разного уровня. Но, к сожалению, школьная математика явно не предусматривает обучение решению задач в целых числах. Это порождает так называемые пробелы и "дырки" в знаниях учеников по математике. Так как мы заинтересованы в получении наиболее высокого балла на экзамене, то нам необходимо систематизировать уже имеющиеся представления по данной теме, пополнить «багаж» знаний детей теоремами и задачами, которые мы не изучали на уроках математики, но они необходимые для решения подобных задач. Также изучить и разобрать базовые задачи (опорные задачи) и на их основе научиться решать более сложные задачи.

Проанализировав программу по математике в связи с ежегодным изменением тестов ЕГЭ, я пришла к выводу, что уже с 5-го класса необходимо начинать подготовку. Изучая темы “Деление с остатком”, “Проценты”, я уже разбираю с детьми решения задач типа №1 ЕГЭ. В 6-м классе при изучении тем “Координаты. Координатная плоскость”, “Диаграммы” рассматриваются задания типа №2, "НОД и НОК натуральных чисел" рассматриваются задания типа №19.

Цель работы: изучение наибольшего общего делителя и наименьшего общего кратного натуральных чисел, применение данных знаний в решении задачи №19 ЕГЭ, освоение методов решения задач такого типа.

Задачи

1) Описать основные базовые задачи;

2) На основе базовых задач решать более сложные задачи , разлагая их по базовым задачам;

3) Сформулировать алгоритм решения задач КИМ ЕГЭ типа №19.

Гипотеза

Углубление изучения исследований по данной теме могут вывести на такой уровень, что можно справиться на экзамене с заданием типа №19

Объектом исследования является класс теоретико-числовых задач, решаемых в целых числах, предметом исследования – технология базовых задач в целых числах.

Практическая значимость: рассмотрены интересные задачи на нахождение НОД и НОК, приведены примеры решения задачи № 19 ЕГЭ

Структура работы определяется последовательностью решения задач исследования. Работа состоит из введения, двух глав, заключения, списка использованной литературы.

Глава I. Теоретические основы вычисления НОД и НОК.

1.1. НОД и НОК

В дальнейшем, целые числа будут обозначаться латинскими буквами a, b, c и т.д. Определим важное понятие делимости чисел.

Определение 1. Говорят, что целое число а делится на целое число b≠0, если найдется целое число с, удовлетворяющее равенству:

a=bc

Например, число 111 делится на 37, а 28 делится на - 4, ведь 111= 37·3, а 28= (-7) ·(-4). Любое натуральное число всегда делится на 1 и на само себя, ведь a=a·1.

Определение 2. Если целое число а делится на целое число b, то b называется делителем, а а делимым, а для обозначения этого отношения используем символ b|a.

Например:

- число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;

12 - делимое, 1,2,3,4,6,12 - делители

- число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.

36 - делимое, 1,2,3,4,6,12,18,36 - делители

Делитель натурального числа a - это такое натуральное число, которое делит данное число a без остатка. Натуральное число, которое имеет более двух делителей, называется составным. Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12. Наибольший из делителей этих чисел - 12.

Пусть 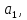... , 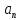- ненулевые целые числа. Целое число К называется общим кратным чисел 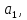... , , 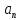если оно кратно каждому из этих чисел.

Определение 3. Наименьшее из положительных общих кратных называется наименьшим общим кратным чисел ... , .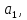

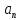Множество общих кратных чисел 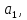... , 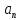будет обозначаться символом М {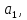... , 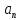}, а их наименьшее общее кратное - НОК (... , ).

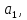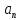Например, числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 – тоже их общие кратные. Среди всех общих кратных всегда есть наименьшее, в данном случае это 90.

Определение 4. Наибольшим общим делителем совокупности целых чисел называется наибольшее положительное число, делящее каждое из этих чисел.

Множество всех общих делителей чисел 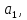... , 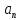будет обозначаться символом D{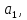... , 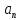}, а их наименьшее общее кратное - НОД (... , ).

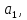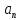 Целые числа называются взаимно простыми, если их наибольший общий делитель равен 1.

Например, найдем все делители чисел 6, 10 и 15

D (6) = {±1, ± 2, ± 3, ± 6}

D (10) = {±1, ± 2, ± 5, ±10}

D (15) = {±1, ± 3, ± 5, ±15}

НОД (6,10,15) = 1

Значит, числа 6, 10, 15 взаимно просты.

1.2. Алгоритм Евклида.

Пусть  ≥  - натуральные числа, требуется найти (а, b) - их наибольший общий делитель.

Придуманный в Древней Греции алгоритм, называемый алгоритмом Евклида, достаточно быстро находит наибольший общий делитель.

Лемма

1. Если а - целое, b - натуральное и b|a, то множество общих делителей чисел а и b совпадает с множеством делителей b.

В частности (а, b)= b.

2. Если 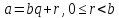, то D{ а, b } = D{ b, r }

Пусть  и  — целые числа, не равные одновременно нулю, и последовательность чисел не равные одновременно нулю, и последовательность чисел

определена тем, что каждое  — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть:

Тогда НОД(a, b), наибольший общий делитель a и b, равен , последнему ненулевому члену этой последовательности.

Пример 1: Найти наибольший общий делитель чисел 3009 и 894.

Пользуясь алгоритмом Евклида находим:

3009= 894 ·3+327 894=327·3+240

327=240·1+87 240=87·2+66

87=66·1+21 66=21·3+3

21=3·7

Значит, НОД(3009, 894) = 3

Пример 2: Найти наибольший общий делитель чисел 64 и 48.

Воспользуемся алгоритмом Евклида. В этом примере a=64, b=48.

Делим 64 на 48, получаем 64:48=1 (ост. 16) , что можно записать в виде равенства64=48·1+16, то есть, q₁=1, r₁=16.

Теперь делим b на r₁, то есть, 48 делим на 16, получаем 48:16=3, откуда имеем 48=16·3.

Здесь q₂=3, а r₂=0, так как 48 делится на 16 без остатка.

Мы получили r₂=0, поэтому это был последний шаг алгоритма Евклида, и r₁=16является искомым наибольшим общим делителем чисел 64 и 48.

1.3. Нахождение НОД и НОК с помощью разложения на простые множители

  Также, для того, чтобы найти  наибольший общий делитель, можно разложить каждое из заданных чисел на простые множители.

Определение 1. НОД двух целых положительных чисел a и b равен произведению всех общих простых множителей, находящихся в разложениях чисел a и b на простые множители.

Необходимо выписать отдельно только те множители, которые входят во все заданные числа, причём из двух показателей степени этого множителя берётся наибольший. Потом перемножаем между собой выписанные числа – результат перемножения и есть наибольший общий делитель.

Приведем пример для пояснения правила нахождения НОД. Пусть нам известны разложения чисел 220 и 600 на простые множители, они имеют вид 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими простыми множителями, участвующими в разложении чисел 220 и 600, являются 2, 2 и 5. Следовательно, НОД (220, 600)=2·2·5=20.

Таким образом, если разложить числа a и b на простые множители и найти произведение всех их общих множителей, то этим будет найден наибольший общий делитель чисел a и b.

 Разберем пошагово вычисление наибольшего общего делителя:

     1. Разложить делители чисел на простые множители:

Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа - делитель. Далее в левом столбце записываем значения частных. Поясним сразу на примере. Разложим на простые множители числа 28 и 64.

     2. Подчёркиваем одинаковые простые множители в обоих числах:

28 = 2 • 2 • 7

64 = 2 • 2 • 2 • 2 • 2 • 2

     3. Находим произведение одинаковых простых множителей и записываем ответ:

НОД (28; 64) = 2 • 2 = 4

Ответ: НОД (28; 64) = 4

Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».

Первый способ записи НОД:

Найти НОД 48 и 36.

НОД (48; 36) = 2 • 2 • 3 = 12

 Второй способ записи НОД:

Теперь запишем решение поиска НОД в строчку. Найти НОД 10 и 15.

Д (10) = {1, 2, 5, 10}

Д (15) = {1, 3, 5, 15}

Д (10, 15) = {1, 5}

НОД (10; 15) = 5

Определение 2. НОК содержит все простые множители, входящие хотя бы в одно из разложений чисел a, b, причём из двух показателей степени этого множителя берётся наибольший. 

Пример:

НОК

Правило. Чтобы найти НОК ряда чисел, нужно:

— разложить числа на простые множители;

— перенести во множители искомого произведения самое большое разложение (произведение множителей самого большого числа из заданных), а потом добавить множители из разложения других чисел, которые не встречаются в первом числе или стоят в нем меньшее число раз;

— полученное произведение простых множителей будет НОК заданных чисел.

Любые два и более натуральных чисел имеют свое НОК. Если числа не кратны друг другу или не имеют одинаковых множителей в разложении, то их НОК равно произведению этих чисел.

Пример 1:

Простые множители числа 28 (2, 2, 7) дополнили множителем 3 (числа 21), полученное произведение (84) будет наименьшим числом, которое делится на 21 и 28.

Пример 2:

Простые множители наибольшего числа 30 дополнили множителем 5 числа 25, полученное произведение 150 больше самого большого числа 30 и делится на все заданные числа без остатка. Это наименьшее произведение из возможных (150, 250, 300...), которому кратны все заданные числа.

Пример 3:

Числа 2,3,11,37 — простые, поэтому их НОК равно произведению заданных чисел.

 Правило. Чтобы вычислить НОК простых чисел, нужно все эти числа перемножить между собой.

Еще один вариант:

Чтобы найти наименьшее общее кратное (НОК) нескольких чисел нужно:

 1)  представить каждое число как произведение его простых множителей, например:

504 = 2 · 2 · 2 · 3 · 3 · 7 ,

2)  записать степени всех простых множителей:

504 = 2 · 2 · 2 · 3 · 3 · 7 = 2³ · 3² · 7¹,

3)  выписать все простые делители (множители) каждого из этих чисел;   

  4)  выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;

5)  перемножить эти степени.

Пример .  Найти НОК чисел: 168, 180 и 3024.

Решение .        168 = 2 · 2 · 2 · 3 · 7 = 2³ · 3¹ · 7¹ ,

                        180 = 2 · 2 · 3 · 3 · 5 = 2² · 3² · 5¹ ,

                        3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 2⁴  · 3³  · 7¹ .

Выписываем наибольшие степени всех простых делителей и перемножаем их: НОК = 2⁴ · 3³ · 5¹ · 7¹ = 15120.

Глава II. Методический опыт, практическое применение НОД и НОК

2.1. Как НОК и НОД чисел помогает решать интересные и

разнообразные задачи

Меня заинтересовали необычные задачи, и я решила поподробнее изучить использование НОК и НОД чисел при решении разнообразных задач.

Оказывается, есть задачи_, в которых, на первый взгляд, эти понятия и не используются, а на самом деле с их помощью легко решаются.

При исследовании вопроса об использовании НОК и НОД чисел я распределила все задачи на следующие группы:

-решение текстовых задач;

-задачи на сократимость дробей;

-задачи на вычисление НОК и НОД чисел;

-задачи на доказательство утверждений;

-решение уравнений;

-решение систем уравнений;

-построение графиков функций.

Коротко опишу, на чем основано решение каждого вида задач.

Текстовые задачи решаются на основе определения понятий и их свойств. Какой либо алгоритм решения трудно предложить, но в основном нужно опираться на логику вопроса.

Пример №1

Туристы проехали за 1 день 56 км, а за 2-72км, причем их скорость была одинаковой и выражалась целым числом км/ч, и каждый день они были в пути целое число часов. Найдите скорость, с которой ехали туристы, если она была наибольшей из удовлетворяющих условию задачи.

Решение.

Очевидно, нужно найти НОД (56;72)
56=2*2*2*7; 72=3*3*2*2*2

НОД(56;72)=8

Скорость равна 8 км/ч Ответ: 8 км/ч.

Пример №2

На столе лежат книги, число которых меньше, чем 100. Сколько лежит книг, если известно, что их можно связывать пачки по 3, по 4, и по 5 штук?

Решение.

Очевидно, нужно найти НОК (5;4;3)

НОК (5;4;3)=3*4*5=3*20=60.

Ответ: 60 штук.

Пример №3

Теплоход «Суворов» свой рейс туда и обратно совершает за 8 дней, теплоход «Горький» за 12 дней, а теплоход «Киров» за 18 дней. Через сколько дней теплоходы снова встретятся в порту, если они ушли в рейс одновременно?

Решение.

Найдем НОК(8;12;18), для этого разложим на множители числа 24=2x2x2x2x3, 18=2x3x3.

Имеем: НОК(8;12)=24,а НОК(8;12;18)=НОК(24;18)=24хЗ=72(дня).

Ответ: теплоходы встретятся через 72 дня.

Задачи на сократимость дробей можно решить несколькими способами:

1. Разложением на множители числителя и знаменателя;

2. Применение алгоритма Евклида:

3. На основе свойств НОК и НОД чисел;

4. Выделение целой части непосредственным делением числителя на
   знаменатель дроби.

Пример:

Сократить дробь: 5п+7/(3n+2), если nЄNи найти значение, при котором она сокращается.

Решение.

Применим алгоритм Евклида.

НОД (5n+7;3n+2)=d;

5n+7=1*(Зn+2)+2n+5

Зп+2=1*(2n+1)+(n-3)

2п+5=2*(n-3)+11

НОД (5n+7;Зn+2)= НОД (n-3;11)=11,11-простое Соответственно (п-3):11 Имеем значения n= 14 n=25n=36 и.т.д. При n=14 дробь равна: 5n+7/(3n+2)=1,75.Т.е n=11k+3;(kЄN)

Ответ:n=11k+3;(kЄN)

Вычисление НОК и НОД чисел осуществляется на основе разложения чисел на простые множители и использовании свойств НОК и НОД. НОД чисел можно найти, используя алгоритм Евклида.

Пример

Найдите количество всех натуральных делителей числа 10⁹⁹⁹, которые не являются делителями числа 10⁹⁹⁸.

Решение.

Любой делитель числа 10⁹⁹⁹ имеет вид с1=2^р*5^q 0 ⁹⁹⁸, если р или q равны 999. Подсчитаем. 1000 штук

2⁹⁹⁹, 2⁹⁹⁹ *5^,… , 2⁹⁹⁹*5⁹⁹⁹

5^{999 ,} 5⁹⁹⁹ *2,…, 5⁹⁹⁹ *2⁹⁹⁹

Но можно заметить, что d=2⁹⁹⁹5⁹⁹⁹ повторяется 2 раза, то всего делителей будет: 1000+1000-1-1999 (шт)

Ответ: 1999.

При доказательстве большинства утверждений можно использовать единый подход, а именно:

1. Непосредственное использование алгоритма Евклида;

2. Перебор возможных случаев.

Например, доказать что НОД(а;b) меньше или равен НОК(а:b).Рассмотрим несколько случаев:

А) а больше b:

Б) а = b;

В) а меньше b и делаем соответствующие выводы на основе свойств рассматриваемых понятий.

Пример №1. Числа k и b -взаимно просты, а их НОК равен 48.Найдите эти числа.

Решение:

Раскладываем 48 на множители: 1*48;2*24;3*16;4*12;6*8 (затем повторение)

Найдем из них взаимно простые: НОД(1 ;48)=1 ,НОД(3; 16)=1

Ответ: k=1, b=48(b=1, k=48)

Или k=3, b=16(b=3, k=16)

Пример №2. Доказать, что п-1 и п и любые 2 последовательных натуральных числа взаимно просты.

Доказательство.

Пусть НОД(п-1;п)=d, тогда их разность делится на d п-(п-1)=1,а это лишь возможно при d=1т.е. эти числа взаимно просты.

При решении уравнений нужно постараться применить метод разложения на множители, и сделать перебор возможных случаев.

При решении систем уравнений постараться, как и в уравнениях осуществить разложение на множители в виде произведения двух натуральных чисел вида dn и dm , где а =dn , b= dm , где d-делитель чисел aиb, m и n -взаимно простые числа и, используя общие методы решения систем, а также свойства НОК и НОД чисел найти соответствующие пары решений системы.

Пример 1. Решить уравнение. НОК(а;6)=18

Решение.

Соответственно, число а имеет вид: а=2*3*3=18; НОД(а;6)=18=2*3*3=18 или следующий: а=3*3=9.

Ответ: а=18 или а=9

Пример 2. Решить уравнение НОД (а;8)=4

Решение.

Число а имеет вид: а=2*2*n (n-нечётное) Соответственно отсюда можно найти т.к дополняя множителями делящимися на 2 мы увеличиваем НОД, т.е. значения а-бесконечно.

а=2*2*1=4,

а=2*2*3=12,

а=2*2*5=20 и.т.д

Т.е n=2k-1 (k-натуральное)

2.2. Примеры решения задач № 19 ЕГЭ через нахождение

НОД и НОК

Пример 1. Мно­же­ство А со­сто­ит из на­ту­раль­ных чисел. Ко­ли­че­ство чисел в А боль­ше семи. Наи­мень­шее общее крат­ное всех чисел из А равно 210. Для любых двух чисел из А их наи­боль­ший общий де­ли­тель боль­ше еди­ни­цы. Про­из­ве­де­ние всех чисел из А де­лит­ся на 1920 и не яв­ля­ет­ся квад­ра­том ни­ка­ко­го це­ло­го числа. Найти числа, из ко­то­рых со­сто­ит А.

Ре­ше­ние.

Наи­мень­шее общее крат­ное чисел, со­став­ля­ю­щих мно­же­ство А. 210 = 2 · 3 · 5 · 7. По­это­му числа, со­став­ля­ю­щие мно­же­ство А — это де­ли­те­ли 210. Все де­ли­те­лей 16:

1,2,3,5,7,2 · 3,2 · 5,2 · 7,3 · 5,3 · 7,5 · 7,2 · 3 · 5,2 · 3 · 7,2 · 5 · 7,3 · 5 · 7,2 · 3 · 5 · 7

Каж­дый де­ли­тель со­дер­жит не более од­но­го мно­жи­те­ля 2. А про­из­ве­де­ние всех чисел из А де­лит­ся 1920 = 2⁷ · 3 · 5. По­это­му среди чисел, со­став­ля­ю­щих А, долж­но быть, по край­ней мере семь чет­ных, а их всего во­семь:

 2,2 · 3,2 · 5,2 · 7,2 · 3 · 5,2 · 3 · 7,2 · 5 · 7,2 · 3 · 5 · 7

Если число 2 вхо­дит в А, то любое дру­гое число из А долж­но де­лит­ся на 2. Зна­чит, А={2,6,10,14,30,42,70,210},

но про­из­ве­де­ние этих чисел равно 2⁸ · 3⁴ · 5⁴ · 7⁴ = (2⁴ · 3² · 5² · 7²)².

Зна­чит, 2 не вхо­дит в А, а числа

 2 · 3,2 · 5,2 · 7,2 · 3 · 5,2 · 3 · 7,2 · 5 · 7,2 · 3 · 5 · 7

вхо­дят в А, но их всего семь. По­это­му этот набор нужно рас­ши­рить, до­бав­ляя де­ли­те­ли 210, не вза­им­но про­стые со всеми ука­зан­ны­ми семью чис­ла­ми. Такой де­ли­тель един­ствен­ный — 3 · 5 · 7.

 Ответ: А = {6,10,14,30,42,70,105,210}

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 19.11.2009 с решениями: ва­ри­ант 2. (Часть С)

Пример 2. Пусть q — наи­мень­шее общее крат­ное, а d — наи­боль­ший общий де­ли­тель на­ту­раль­ных чисел x и y, удо­вле­тво­ря­ю­щих не­ра­вен­ству 3x = 8y − 29.

а) Может ли  быть рав­ным 170?

б) Может ли  быть рав­ным 2?

в) Най­ди­те наи­мень­шее зна­че­ние  .

Ре­ше­ние.

а) Для чисел x = 17 и y = 10 вы­пол­ня­ет­ся усло­вие 3x = 8y −29, q = 170, d = 1,  = 170

б) и в) При x = 1 и y = 4 вы­пол­ня­ет­ся ра­вен­ство 3x = 8y − 29 и  = 4.  По­ка­жем, что ни­ка­кое зна­че­ние  не ре­а­ли­зу­ет­ся.

Если x = y, то x=y=  что не­воз­мож­но, по­сколь­ку числа x и y — на­ту­раль­ные. Пусть для опре­делённо­сти x y и x = ad, a y = bd. Тогда на­ту­раль­ные числа a и b вза­им­но про­сты и a  b. По­лу­ча­ем   от­ку­да Если  то a = b, что не­воз­мож­но.

Если  то a = 1, b = 2 и, зна­чит, y = 2x, от­ку­да  что не­воз­мож­но.

Если  то a = 1, b = 3 и, зна­чит, y = 3x, от­ку­да  что не­воз­мож­но.

Ответ: а) да; б) нет) в) 4.

Источник: Ти­по­вые тестовые за­да­ния по математике, под ре­дак­ци­ей И. В. Ященко. 2016 г.

Пример 3. По кругу в не­ко­то­ром по­ряд­ке по од­но­му разу на­пи­са­ны числа от 9 до 18. Для каж­дой из де­ся­ти пар со­сед­них чисел нашли их наи­боль­ший общий де­ли­тель.

а) Могло ли по­лу­чить­ся так, что все наи­боль­шие общие де­ли­те­ли равны 1?

б) Могло ли по­лу­чить­ся так, что все наи­боль­шие общие де­ли­те­ли по­пар­но раз­лич­ны?

в) Какое наи­боль­шее ко­ли­че­ство по­пар­но раз­лич­ных наи­боль­ших общих де­ли­те­лей могло при этом по­лу­чить­ся?

Ре­ше­ние.

а) Да, могло. На­при­мер, если числа за­пи­са­ны в по­ряд­ке 9, 16, 15, 14, 13, 12, 11, 18, 17, 10.

б) Всего по кругу за­пи­са­но 10 чисел. Для каж­дой пары со­сед­них чисел мы ищем наи­боль­ший общий де­ли­тель, сле­до­ва­тель­но, по­лу­чим 10 наи­боль­ших общих де­ли­те­лей. Если они все по­пар­но раз­лич­ны, то хотя бы один из них не мень­ше 10. Но та­ко­го быть не может, так как для дан­ных чисел наи­боль­ший из все­воз­мож­ных наи­боль­ших общих де­ли­те­лей есть НОД(18, 9) = 9.

в) Числа 11, 13 и 17 яв­ля­ют­ся про­сты­ми, наи­боль­шие общие де­ли­те­ли этих чисел со всеми осталь­ны­ми чис­ла­ми рав­ня­ют­ся 1. Каж­дое из чисел имеет двух со­се­дей, сле­до­ва­тель­но, хотя бы два числа из этих трёх будут иметь по край­ней мере од­но­го со­се­да, от­лич­но­го от этих трёх чисел. Таким об­ра­зом, хотя бы че­ты­ре из всех наи­боль­ших общих де­ли­те­лей будут рав­нять­ся 1, то есть сов­па­дать. Сле­до­ва­тель­но, не может быть боль­ше, чем семь по­пар­но раз­лич­ных наи­боль­ших общих де­ли­те­лей, по­сколь­ку всего их де­сять, причём че­ты­ре сов­па­да­ют. Для рас­ста­нов­ки 9, 18, 12, 16, 14, 13, 11, 17, 10, 15 по­лу­ча­ет­ся ровно 7 по­пар­но раз­лич­ных наи­боль­ших общих де­ли­те­лей.

 Ответ: а) Да; б) нет; в) семь.

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 13.03.2014 ва­ри­ант МА10505.

Пример 4. Сумма двух на­ту­раль­ных чисел равна 43, а их наи­мень­шее общее крат­ное в 120 раз боль­ше их наи­боль­ше­го об­ще­го де­ли­те­ля. Най­ди­те эти числа.

Ре­ше­ние.

Сумма чисел крат­на их наи­боль­ше­му об­ще­му де­ли­те­лю, по­это­му их наи­боль­ший общий де­ли­тель яв­ля­ет­ся де­ли­те­лем числа 43, от­ку­да сле­ду­ет, что он равен 1. Тогда наи­мень­шее общее крат­ное этих чисел равно их про­из­ве­де­нию. Обо­зна­чив ис­ко­мые числа х и у, по­лу­ча­ем си­сте­му

решая ко­то­рую, по­лу­ча­ем числа 40 и 3.

Ответ: 40 и 3.

Источник: ЕГЭ по ма­те­ма­ти­ке 03.06.2013. Ос­нов­ная волна. Урал. Ва­ри­ант 203

Заключение

При выборе темы работы меня в первую очередь заинтересовала актуальность темы, так как я поняла, что из всех заданий ЕГЭ самое сложное для меня это задание №19 ЕГЭ. Так как школьная программа не уделяет должного внимания этой непростой теме, то я и стала изучать её самостоятельно.

В ходе работы по данной теме я рассмотрела основные базовые задачи нахождения НОД и НОК чисел и на их основе начала решать боле сложные задания. Изучила наибольший общий делитель и наименьшее общее кратное натуральных чисел, научилась применять данные знания в решении задачи №19 ЕГЭ, освоила методы решения задач такого типа.

Таким образом, задачи, поставленные в начале работы, были решены, цель исследования достигнута, гипотеза подтверждена.

Список использованных источников

1.Богатырев С.В.., А.А Максютин, Ю.Н. Неценко, С.Ю. Попов, Т.П. Шаповалова. 9. Тренировочные материалы для подготовки к ЕГЭ по математике 2010 Учебное пособие. Сост. – Самара: ГОУ СИПКРО, 2010 – 124с.

3. Корянов А.Г. Математика ЕГЭ 2010. Задания С6 "Уравнения и неравенста в целых числах"

7. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: 
Учеб. пособие для 10 кл. сред. шк. – М.: Просвещение, 1989. 

8. Ященко И. В.. – М.: Издательство «Экзамен»,2011. 

20