Непрерывность и пределы функций

Глава 1 Непрерывность и пределы функций

Различие между описательно-интуитивными и строгими математическими определениями. Понятие предела функции. Вычисление пределов. Построение графиков функций.

Пункт 1. Непрерывность функций

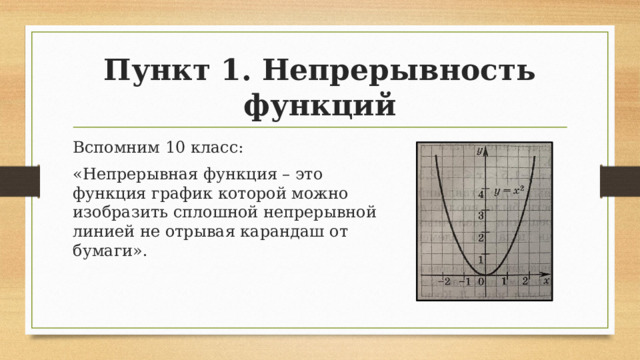
Вспомним 10 класс:

«Непрерывная функция – это функция график которой можно изобразить сплошной непрерывной линией не отрывая карандаш от бумаги».

Пример (применение непрерывности)

Решить неравенство:

• Найти ОДЗ + нули числителя и знаменателя
• Отметить найденные границы с учётом знака неравенства
• Определить знаки функции на отмеченных промежутках и провести кривую знаков
• Записать ответ

Ответ:

Вспомним…

Определение. Функция называется возрастающей на множестве S , если для любых двух чисел и , принадлежащих этому множеству, из следует .

А всегда ли можно изобразить график функции по определению «непрерывного карандаша»…?

Попробуем обойти проблему бесконечности!

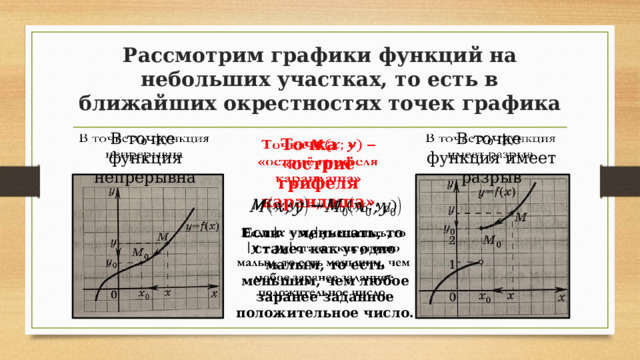
Рассмотрим графики функций на небольших участках, то есть в ближайших окрестностях точек графика

В точке функция непрерывна

В точке функция имеет разрыв

Точка – «остриё грифеля карандаша»

Если уменьшать, то станет как угодно малым, то есть меньшим, чем любое заранее заданное положительное число.

Определение непрерывности на математическом языке (строгое математическое определение)

Определение. Функция называется непрерывной в точке , если для любого числа существует такое число , что . (определение О. Коши)

– «эпсилон»

– «дельта»

Основывается на понятии сколь угодно малого!!!

Пример (непрерывность в любой точке)

Доказать, что функция непрерывна в любой точке .

Идея: нам нужно, для произвольного числа найти такое , чтобы из неравенства .

Итак: для любого при , из неравенства следует неравенство , что и означает, согласно определению, непрерывность функции в точке .

Пример (непрерывность в точке )

Доказать непрерывность функции в точке .

Идея: нам нужно, для произвольного числа найти такое , чтобы из неравенства .

Рассмотрим окрестность точки

Для любого

Пример (непрерывность в точке )

Для любого , взяв , получаем:

Из того, что следует:

Итак: для любого при , из неравенства следует неравенство , что и означает, согласно определению, непрерывность функции в точке .

Замечание!

Когда речь идёт о границах отрезка, который является областью определения функции, то определение непрерывности функции в точке НЕПРИМЕНИМО!

При и при

неравенство , где

ТЕРЯЕТ СМЫСЛ!

Функция не определена на и

Вывод из замечания:

Односторонняя непрерывность.

Необходимо в определении непрерывности убрать модуль из неравенства .

Непрерывность справа :

Непрерывность слева :

Определение. Функция, непрерывная во всех точках промежутка, является на этом промежутке непрерывной.

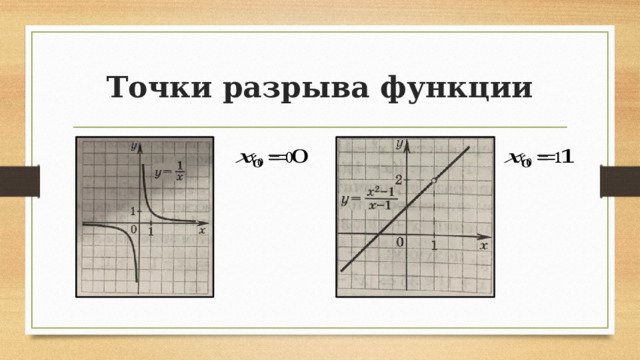
Точки разрыва функции

Точки разрыва функции

Определение. Точку входящую в область определения функции, называют точкой разрыва функции, если функция в ней не является непрерывной.

Определение. Точку , не входящую в область определения функции, называют точкой разрыва функции, если и слева, и справа от неё как угодно близко к точке есть точки, в которых функция определена.

Внимание вопрос! Почему у функции в точке бесконечный разрыв, а у функции в точке – устранимый разрыв?

Пример (устранение разрыва функции)

Устранить разрыв – это значит найти непрерывную функцию, которая совпадает с данной функцией во всех точках, кроме точке разрыва.

Устранить разрыв функции

Разрыв в точке .

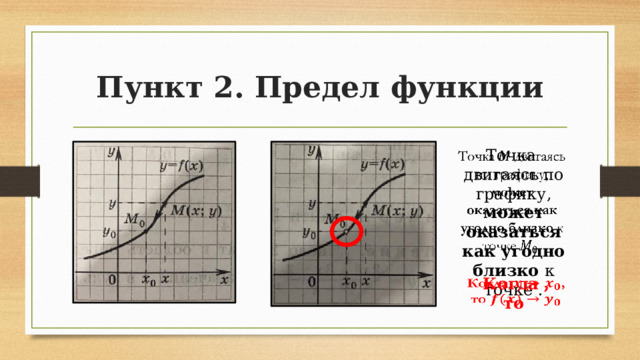
Пункт 2. Предел функции

Точка двигаясь по графику, может оказаться как угодно близко к точке .

Когда ,

то

Что значит «стремится»

В русском языке:

«Стремится» - это процесс приближения к некоторой цели, но н само её достижение.

В математическом языке:

« стремится к » – значит, что принимает значения сколь угодно близкие, но не равные .

Математики говорят о пределе)

Когда при стремлении к , стремится к , то говорят о пределе и пишут:

Читаем так: «Предел при , стремящемся к , равен »

– сокращение от латинского слова , которое в переводе означает граница, предел.

Предел на языке и

Определение. Функция имеет в точке предел, равный , если для любого существует такое , что

.

Важно!!!

Предел в точке имеют только те функции, которые в этой точке или непрерывны, или имеют устранимый разрыв .

Что это значит…

Если функция непрерывна в точке , то и

Обратно:

Если , то функция непрерывна в точке .

Если в точке - устранимый разрыв, то сначала его устраняем.

Пример (нахождения предела непрерывной функции)

Найти

1. В точке функция непрерывна.

2. Подставляем в функцию:

Ответ: 3

Пример (нахождения предела функции с устранимой точкой разрыва)

Найти

1. Число 2 точка устранимого разрыва.

2. Устраняем разрыв.

3. Находим предел:

Ответ: 1,25

Односторонний предел

Определение. Функция имеет в точке правый предел , равный , если для любого существует такое , что

.

Определение. Функция имеет в точке левый предел , равный , если для любого существует такое , что

.

Условие существования правого предела

Условие существования левого предела

Обозначение пределов

Правосторонний (правый) предел –

Левосторонний (левый)предел –

Двусторонний предел (просто предел) –

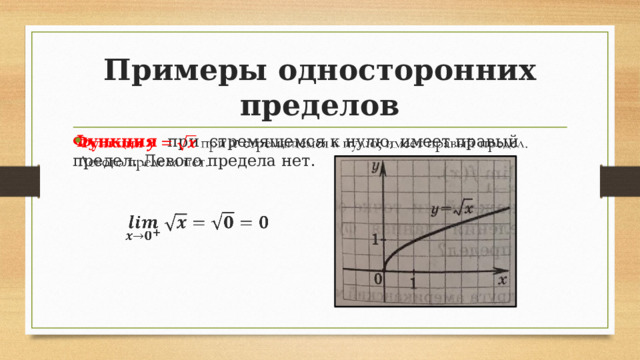
Примеры односторонних пределов

Функция при стремящемся к нулю, имеет правый предел. Левого предела нет.

Примеры односторонних пределов

Функция имеет как правый, так и левый предел в точке .

- не существует

Выводы:

• Двусторонний предел может не существовать
• Правый и левый предел могут не совпадать
• Функция может обладать только одним видом предела

Специальные символы (кванторы) математического анализа

Квантор общности (от англ. all) – «» (заменяет слова: все, всё, для всякого, любой)

Квантор существования (от англ. exists) – «» (заменяет слова: существует, найдётся)

Задание: прочитайте предложение

, такое что,